PINNs全面基准测试 |
您所在的位置:网站首页 › 多元函数微分逆问题 › PINNs全面基准测试 |
PINNs全面基准测试
|
前言 1、本号将持续更新AI4PDEs&AI4CFD相关前沿进展 2、本号主推:开源、启发性的文献 3、感兴趣可以关注微信公众号:AI4CFD 4、持续更新中!

摘要:尽管在物理信息神经网络(PINNs)上取得了重大进展,但这些方法在广泛的偏微分方程(PDEs)范围内的全面比较仍然缺失。本研究介绍了PINNacle,这是一个旨在填补这一空白的基准测试工具。PINNacle提供了一个多样化的数据集,包括来自各个领域的20多种不同PDEs,涵盖了热传导、流体动力学、生物学和电磁学等。这些PDEs包含了现实世界问题固有的关键挑战,如复杂几何形状、多尺度现象、非线性和高维度。PINNacle还提供了一个用户友好的工具箱,集成了约10种最先进的PINN方法,用于系统评估和比较。我们已经对这些方法进行了广泛的实验,提供了关于它们优缺点的见解。除了提供一种标准化的性能评估手段外,PINNacle还提供了深入分析,以指导未来研究,特别是在领域分解方法和损失重新加权等方面,以处理多尺度问题和复杂几何形状。据我们所知,这是最大的具有多样性和全面评估的基准,无疑将促进PINNs的进一步研究。 1 介绍偏微分方程(PDEs)在科学和工程中具有至关重要的地位,因为它们通常是我们理解复杂物理系统(如流体流动、热传导和应力分布)的基础(Morton & Mayers, 2005)。对PDE系统的计算模拟长期以来一直是研究的焦点,这促进了如有限差分(Causon & Mingham, 2010)、有限元(Reddy, 2019)和有限体积方法(Eymard et al., 2000)等数值方法的发展。 近期的进展使得深度神经网络被用来解决涉及PDEs的正向和逆向问题(Raissi et al., 2019; Yu et al., 2018; Daw et al., 2017; Wang et al., 2020)。在这些中,物理信息神经网络(PINNs)作为一种有希望的替代传统数值方法解决此类问题的方式,已经显现出来(Raissi et al., 2019; Karniadakis et al., 2021)。PINNs利用底层的物理法则和可用数据有效地处理各种科学和工程应用。这一领域日益增长的兴趣促进了众多PINN变种的发展,每个变种都旨在克服特定的挑战或增强原始框架的性能。 尽管PINN方法取得了显著进展,但目前缺乏这些方法在多种类型的PDEs上的全面比较。建立这样一个基准至关重要,因为它可以使研究者更彻底地理解现有方法并指出潜在的挑战。尽管有几项研究比较了采样方法(Wu et al., 2023)和重新加权方法(Bischof & Kraus, 2021),但尚未有协调一致的努力来开发一个使用来自现实世界问题的挑战性数据集的严格基准。PDEs的种类繁多和固有的复杂性使得进行全面分析变得困难。此外,不同的数学属性和应用场景进一步增加了任务的复杂性,要求基准测试既要具有适应性又要全面。 为了解决这些挑战,我们提出了PINNacle,一个用于评估和理解PINNs性能的综合性基准测试。如图1所示,PINNacle包含三个主要组成部分 —— 一个多样化的数据集、一个工具箱和评估模块。数据集包括来自各个领域的20多种不同PDEs的任务,涵盖了热传导、流体动力学、生物学和电磁学等。每个任务都带来了自己的一系列挑战,如复杂的几何形状、多尺度现象、非线性和高维度,因此为PINNs提供了一个丰富的测试场地。工具箱整合了10多种最先进(SOTA)的PINN方法,使得不同策略之间的系统比较成为可能,包括损失重新加权、变分公式、自适应激活和域分解等。这些方法可以灵活地应用于数据集中的任务,为研究人员提供了一种便捷的方式来评估PINNs的性能,同时也对二次开发友好。评估模块提供了一种标准化的手段来评估不同PINN方法在所有任务上的性能,确保比较的一致性,并促进识别各种方法的优点和缺点。 PINNacle提供了一个强大、多样化和全面的PINNs基准套件,为该领域的理解和应用做出了重大贡献。它代表了PINNs发展演进中的一大步,可能促进这一激动人心领域的更多创新研究和发展。简而言之,我们的贡献可以总结如下: 我们设计了一个数据集, 涵盖了20多个具有挑战性的PDE问题。这些问题涵盖了PINNs面临的几个关键挑战,包括处理复杂几何、多尺度现象、非线性和高维问题等。 我们系统地评估了10多种精心选择的代表性PINNs变体。我们进行了彻底的实验和消融研究,以评估它们的性能。据我们所知,这是最大的比较不同PINN变体的基准。 我们提供了深入的分析,以指导未来的研究。我们展示了使用损失重加权和域分解方法可以提高在多尺度和复杂几何问题上的性能。变分形式在求解反问题时实现了更好的性能。然而,目前很少有方法能够充分解决非线性问题,这表明了未来的探索和发展方向。
图1:PINNacle的架构。它包含了一个覆盖20多个偏微分方程(PDEs)的数据集,一个实现了大约10种最先进(SOTA)方法的工具箱,以及一个评估模块。这些方法应用范围广泛,如流体力学、电磁学、热传导、地球物理学等领域。 2 相关工作 2.1 科学机器学习中的基准和数据集人工智能在科学研究中的应用趋势不断增长,促进了各种基准和数据集的发展,这些基准和数据集在数据格式、大小和管理原则上有很大不同。例如,(Lu等人,2022年)提出了一个用于比较神经算子的基准,而(Botev等人,2021年;Otness等人,2021年)则对学习潜在牛顿力学的方法进行了基准测试。此外,领域特定的数据集和基准在流体力学(Huang等人,2021年)、气候科学(Racah等人,2017年;Cachay等人,2021年)、量子化学(Axelrod&GomezBombarelli,2022年)和生物学(Boutet等人,2016年)中存在。 除了这些领域特定的数据集和基准之外,自从物理信息神经网络(PINNs)的出现以来,物理学上的机器学习引起了相当大的关注(Hao等人,2022年;Cuomo等人,2022年)。这些方法成功地将物理定律纳入模型训练中,展示了在各种科学和工程领域中的巨大潜力。各种论文已经比较了PINN框架内的不同组成部分;例如,(Das&Tesfamariam,2022年)和(Wu等人,2023年)调查了PINN中的点对称方法,而(Bischof&Kraus,2021年)比较了不同损失组件的重新加权技术。PDEBench(Takamoto等人,2022年)和PDEArena(Gupta&Brandstetter,2022年)设计了多个任务,比较了科学机器学习中不同方法,如PINNs、FNO和U-Net。然而,文献中缺乏对各种PINN方法的全面比较。 2.2 软件和工具包已经开发了大量用于用神经网络求解PDE的软件解决方案。其中包括SimNet(Hennigh等人,2021年)、NeuralPDE(Rackauckas&Nie,2017年)、TorchDiffEq(Chen等人,2020年)和PyDEns(Khudorozhkov等人,2019年)。更近期,DeepXDE(Lu等人,2021年)被引入作为一个在不同后端实现中实现PINNs的基础库。然而,目前还没有一个提供高级PINN变体统一实现的工具包。我们的PINNacle通过提供灵活的接口填补了这一空白,这个接口便于实现和评估不同的PINN变体。我们为研究人员提供了清晰简洁的代码,以执行所有问题和方法的基准测试。 2.3 物理信息神经网络的变体由于其在解决正向和反向PDE问题中的卓越性能,PINNs受到了广泛关注。然而,普通的PINNs有许多局限性。研究人员提出了许多PINN变体,以应对与高维度、非线性、多尺度问题和复杂几何有关的挑战(Hao等人,2022年;Cuomo等人,2022年;Karniadakis等人,2021年;Krishnapriyan等人,2021年)。广义地说,这些变体可以被归类为:损失重加权/重新采样(Wang等人,2021a;b;Tang等人,2021年;Wu等人,2023年;Nabian等人,2021年)、创新优化器(Yao等人,2023年)、新的损失函数,如变分公式(Yu等人,2018年;Kharazmi等人,2019年;2021年;Khodayi-Mehr&Zavlanos,2020年)或正则化项(Yu等人,2022年;Son等人,2021年),以及像域分解(Jagtap&Karniadakis,2021年;Li等人,2019年;Moseley等人,2021年;Jagtap等人,2020c)和自适应激活(Jagtap等人,2020b;a)的新架构。这些变体增强了PINN在各种问题上的性能。在这里,我们从每个类别中选择代表性方法,并使用我们的基准数据集进行全面分析,以评估这些变体。 3 PINNACLE: 一个用于PINNs的层次化基准在本节中,我们首先介绍PINNs的基础知识。然后我们介绍数据集(任务)、PINN方法、工具箱框架和评估指标的细节。 3.1 物理信息神经网络的初步知识物理信息神经网络是用于解决偏微分方程(PDEs)的反问题的基于神经网络的方法,这些问题最近引起了广泛关注。具体来说,让我们考虑一个定义在 上的通用偏微分方程(PDE)系统,它可以表示为: 其中 是一个微分算子, 是边界/初始条件。PINN 使用一个带参数 的神经网络 来逼近 。PINN 的目标是最小化以下损失函数: 其中 、 、 是权重。前两项强制执行在 和边界条件上的PDE约束 。最后一项是数据损失,当有数据可用时它是可选的。然而,PINNs有几个固有的缺陷。首先,PINNs优化了一个不平衡的损失项混合体,这可能会阻碍其收敛性,正如(Wang等人,2021a)中所示。其次,非线性或刚性PDEs可能导致优化不稳定(Wang等人,2021b)。第三,普通的MLP可能难以表示多尺度或高维函数。例如,(Krishnapriyan等人,2021)表明,即使在一个简单的对流问题中,普通的PINNs也只适用于一个小的参数范围。为了解决这些挑战,提出了许多PINNs的变体。然而,这些方法缺乏全面的比较,因此迫切需要开发一个基准测试。 为了有效地比较PINN的不同变体,我们策划了一套代表广泛挑战的偏微分方程问题(数据集)。我们选择了来自不同领域的PDEs,以反映它们在科学和工程中的重要性。我们的数据集包括22个独特案例,更多细节见附录B。 Burgers' Equation,对流体力学至关重要,考虑了一维和二维问题。 泊松方程(Poisson's Equation),在数学和物理学中广泛使用,有四种不同的案例。 热方程(Heat Equation),一个时间依赖的PDE,描述了扩散或热传导,展示了四个独特的案例。 纳维-斯托克斯方程(Navier-Stokes Equation),描述黏性流体物质的运动,在三个场景中展示:由盖板驱动的流动(NS2d-C),几何复杂的后退阶梯流(NS2d-CG),和一个时间依赖的问题(NS2d-LT)。 波动方程(Wave Equation),模拟波动行为,在三个案例中展示。 混沌PDEs,展示了两个流行的例子:格雷-斯科特方程(Gray-Scott, GS)和库拉莫托-西瓦申斯基方程(Kuramoto-Sivashinsky, KS)。 高维PDEs,包括高维泊松方程(PNd)和高维扩散或热方程(HNd)。 逆问题,专注于从噪声数据中重建系数场的泊松方程(PInv)和扩散方程(HInv)。 需要注意的是,我们选择了涵盖广泛数学属性的PDEs。这确保了基准测试不会偏向特定类型的PDE。所选的PDE问题引入了几个核心挑战,包括: 复杂几何:许多PDE问题涉及复杂或不规则的几何形状,如围绕障碍物的热传导或波动传播。这些复杂性对PINNs提出了精确边界行为表示的重大挑战。 多尺度现象:在诸如湍流流体流动等情况中,多尺度现象很常见,其中解在不同尺度上显著变化。在多尺度场景下,实现对所有尺度的平衡表示是神经网络偏微分方程(PINNs)面临的挑战。 非线性行为:许多偏微分方程表现出非线性甚至混沌行为,其中初始条件的微小变化可能导致结果大幅度分歧。在非线性偏微分方程上进行优化成为一个引人入胜的问题。 高维度:在量子力学中经常遇到高维度偏微分方程问题,这给PINNs带来了重大挑战,因为“维数灾难”随着每个维度的增加而增加,伴随着高维空间中的数据稀疏等统计问题。 这些挑战之所以被选择,是因为它们在许多实际应用中经常出现。因此,一种方法在应对这些挑战方面的表现,可以作为其整体实用性的可靠指标。表格1详细介绍了数据集、偏微分方程以及与这些问题相关的挑战。我们使用COMSOL 6.0(多物理学,1998年)提供的有限元方法求解器生成具有复杂几何结构的问题的数据,并使用Chebfun(Driscoll等人,2014年)提供的谱方法来处理混沌问题。更多细节可在附录B中找到。 
表1:我们数据集的概览及其挑战。我们总共选择了22个案例来评估PINNs的方法。左图显示了带有这四个挑战的案例的可视化,即复杂几何形状、多尺度、非线性和高维. 
表2:我们PINNacle中方法的概述。√表示该方法潜在地被设计用来解决或在遇到挑战的问题上显示出经验性改进,反之亦然。 3.3 方法与工具箱在进行了广泛的文献综述后,我们概述了各种PINNs方法,以进行比较。然后,我们介绍了我们的PINNacle的高层结构。 3.3.1 方法如上所述,PINNs的变种主要基于损失函数、架构和优化器(Hao等,2022年)。对损失函数的修改可以分为重新加权现有损失和开发新的损失函数,如正则化和变分公式。架构的变体包括使用域分解和自适应激活。 所讨论的方法与表1中突出显示的挑战直接相关。例如,域分解方法在涉及复杂几何和多尺度现象的问题中特别有效。同时,损失重新加权策略擅长解决具有多个损失的问题中的不平衡。我们选择了这些类别中的变种,因为它们对该领域有重大贡献。在这里,我们列出了主要类别和代表性方法,如表2所总结的那样: 损失权重调整/重采样(2~4):PINNs是用混合的偏微分方程残差、边界条件和可用数据损失进行训练的,这些在方程3中显示。各种方法(Wang等人,2021a;2022b;Bischof & Kraus,2021;Maddu等人,2022;Rohrhofer等人,2021)提出了不同的策略来调整这些权重 、 和 在不同的时期或者重采样配置点 和 在方程3中,这些方法间接调整了权重(Wu等人,2023;Nabian等人,2021)。我们选择了三个著名的例子,即,使用梯度范数重权(PINN-LRA)(Wang等人,2021a),使用神经切线核(PINN-NTK)(Wang等人,2022b)和基于残差的重采样(RAR)(Lu等人,2021;Wu等人,2023)。 新型优化器(5):为了处理多尺度目标问题,提出了一些新型优化器(刘等人,2022年;姚等人,2023年)。我们选择了MultiAdam,它能抵抗域规模变化。 新型损失函数(6~7):一些工作引入了像变分公式(Sirignano & Spiliopoulos,2018年;Khodayi-Mehr & Zavlanos,2020年;Kharazmi等人,2021年)和正则化项这样的新型损失函数以提高训练效果。我们选择hp-VPINN(Kharazmi等人,2021年)和gPINN(Yu等人,2022年;Son等人,2021年),这两个是这两个类别中的代表性例子。 新型激活架构(8~10):一些工作提出了各种网络架构,比如使用CNN和LSTM(张等人,2020年;高等人,2021年;任等人,2022年)、自定义激活函数(Jagtap等人,2020a;b)和域分解(Jagtap & Karniadakis,2021年;Shukla等人,2021年;Jagtap等人,2020c;Moseley等人,2021年)。在自适应激活PINNs中,我们选择LAAF(Jagtap等人,2020a)和GAAF(Jagtap等人,2020b)。域分解是一种将整个域划分为多个子域并在这些子域上训练子网络的方法。它对解决多尺度问题很有帮助,但多个子网络增加了训练的难度。XPINNs、cPINNs和FBPINNs(Jagtap & Karniadakis,2021年;Jagtap等人,2020c;Moseley等人,2021年)是三个代表性例子。我们选择FBPINNs,这是一种最新的域分解技术,它应用了域特定的规范化以稳定训练。 3.3.2 工具箱结构我们提供了一个用户友好且简洁的工具箱,用于实现、训练和评估各种PINN变体。具体来说,我们的代码库基于DeepXDE,并提供了一系列封装好的类和函数,以便于进行高级训练和自定义PDEs。这些工具允许采用标准化和流线型的方法来实施各种PINN变体和PDEs的实现。此外,我们还提供了许多辅助功能,包括计算不同的指标、可视化预测和记录结果。 尽管有多种PINNs的统一实现,我们还设计了一个适应性强的多GPU并行训练框架,以提高系统性评估PINN方法的效率。它解决了在多任务上训练的并行化阶段,有效地平衡了多GPU的计算负载。它允许执行更大型和更复杂的任务。简而言之,我们在附录D中提供了一个使用我们的PINNacle框架对两个泊松方程进行训练和评估的示例代码。 3.4 评估为了全面分析PINN解和真实解之间的差异,我们采用多种度量标准来评估PINN变体的性能。通常,我们选择几种在文献中常用的、适用于所有方法和问题的度量标准。我们假设 是预测值,而 是基准真值,其中 是测试样本的数量。具体来说,我们使用 相对误差(L2RE)和 相对误差(L1RE),这是两种最常用的度量标准,用来衡量解的全局质量, 我们还计算了最大误差(简称mERR)、均方误差(MSE)和傅立叶误差(fMSE),以进行预测的详细分析。这三个指标按照以下方式计算: 其中(F)表示(y)的傅立叶变换,而(k_{\min}),(k_{\max})的选择类似于PDEBench(Takamoto等人,2022年)。此外,对于时变问题,调查解决方案随时间的质量是重要的。因此,我们在附录E.2中计算了随时间变化的L2RE误差。 我们评估PINNs相对于数值解算器的参考性能。实验结果使用 相对误差(L2RE)指标,并纳入正文中,而基于上述指标的更全面的结果集在附录E.1中提供。 4 实验 4.1 主要结果我们现在呈现实验结果。除了第4.3节的消融研究和附录E.2外,我们使用0.001的学习率,并训练所有模型20,000个周期。我们重复所有实验三次,并记录平均值和标准差。表3呈现了我们任务上所有方法的主要结果,并展示了它们的平均(L2)相对误差(标准差结果可在附录E.1中找到)。 PINN。我们使用PINN-w来表示训练具有更大边界权重的PINNs。普通PINNs在准确解决复杂物理系统方面存在困难,表明有很大的改进空间。使用10%的L2相对误差(L2RE)作为解决方案成功的阈值,我们发现普通PINN只解决了22个任务中的10个,其中大部分涉及较简单的方程(例如,Burgers-1d-C的1.45%)。它们在面对具有复杂几何形状、多尺度现象、非线性和较长时间跨度的物理系统时遇到了重大困难。这表明直接优化偏微分方程损失和初始/边界条件损失的平均值会导致诸如损失不平衡、次优收敛和有限表达能力等关键问题。 PINN变体。PINN变体提供了不同程度的方法来解决这些挑战。在一些涉及复杂几何和多尺度现象的情况下,涉及损失权重调整和重采样的方法已经显示出改善性能(例如,在Poisson-2d-CG上的1.43%)。这归因于损失权重和采样配置点的配置,这些配置在训练过程中能够适应性地将更多的重量放在更具挑战性的域上。然而,这些方法仍然难以处理波动方程、纳维-斯托克斯方程以及其他具有更高维度或更长时间跨度的案例。作为新型优化器的代表,MultiAdam解决了几个简单案例和混沌GS方程(9.37%),但并没有明显优于其他方法。变分形式的新损失项在解决逆问题方面展现出显著优势(例如,vPINN在HInv上的1.19%),但在前向案例中,与标准PINN的拟合误差相比没有明确改善。架构的变化可以增强表现力和灵活性,以应对具有复杂几何形状和多尺度系统的案例。例如,FBPINN在混沌GS方程上取得了最小的误差(7.99%),而LAAF在Heat-2d-CG上提供了最佳的拟合结果(2.39%)。 讨论。对于与复杂几何形状和多尺度现象相关的挑战,一些方法可以通过实施损失权重调整、新型优化器以及通过自适应激活提高能力等机制来减轻这些问题。这对于Heat和Poisson方程的2D案例是成立的,这些是经典的线性方程。然而,当系统具有更高的维度(Poisson3d-CG)或更长的时间跨度(Heat2d-LT)时,所有方法都无法解决,凸显了与复杂几何形状和多尺度系统相关的困难。 相比之下,像2D Burgers、NS和KS这样的非线性长时间PDEs对大多数方法都是一个挑战。这些方程对初始条件敏感,导致复杂的解空间和PINNs的更多局部最小值(Steger等人,2022)。具有二阶时间导数和周期性行为的波动方程对PINNs来说尤其困难,它们通常变得不稳定,并可能违反守恒定律(Jagtap等人,2020c;Wang等人,2022a)。尽管所有方法在Poisson-Nd上表现良好,但只有使用LBFGS的PINN解决了Heat-Nd,这表明了二阶优化器解决高维PDEs的潜力(唐等人,2021) 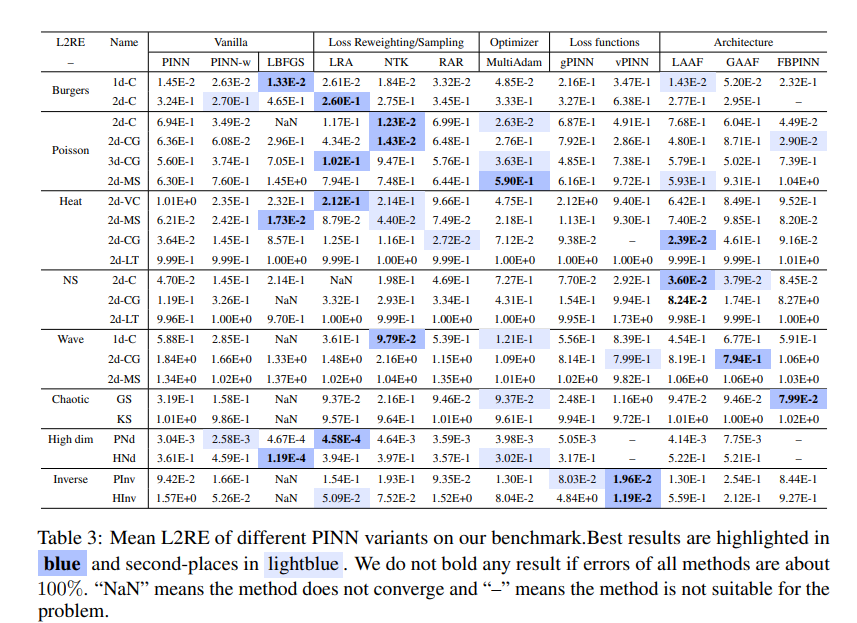
表3:我们基准测试中不同PINN变体的平均L2RE(L2范数相对误差)。最佳结果以蓝色高亮显示,第二名以浅蓝色高亮。如果所有方法的误差大约都是100%,我们不加粗任何结果。“NaN”表示方法没有收敛,“—”表示该方法不适用于该问题。 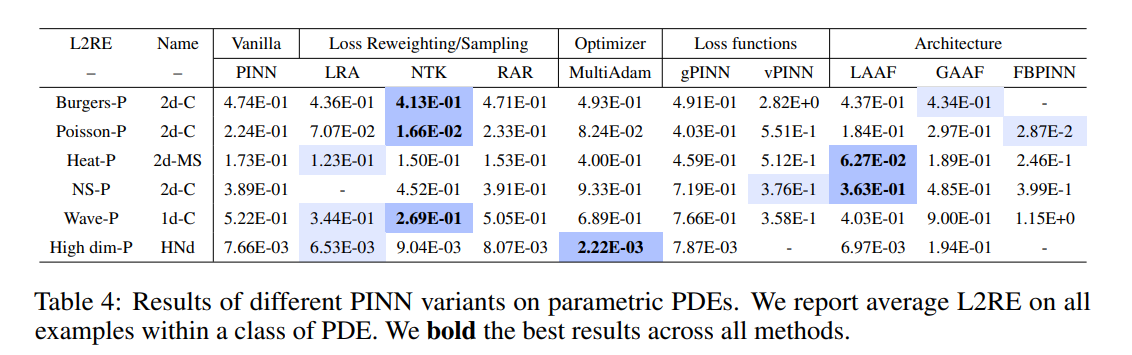
表4:不同PINN变体在参数化偏微分方程上的结果。我们报告了PDE类别内所有示例的平均L2RE(L2范数相对误差)。我们将所有方法中的最佳结果加粗显示。 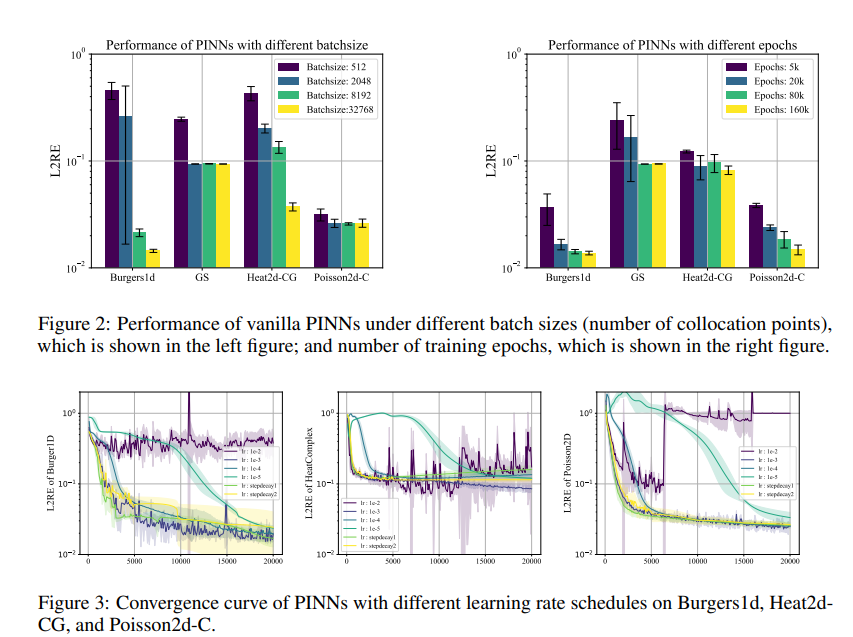 4.2 参数化PDE实验
4.2 参数化PDE实验
PINNs的性能也受到PDE参数的影响(Krishnapriyan等,2021)。为了研究PINNs能否处理一类PDEs,我们设计了这个实验来解决具有不同参数的相同PDEs。我们选择了6个PDEs,即Burgers2d-C,Poisson2d-C,Heat2d-MS,NS-C,Wave1d-C和Heat-Nd(HNd),每个案例包含五个参数化示例。参数化PDE的详细信息见附录B。在这里,我们报告了每种情况下这些参数化PDE的平均L2RE度量,并在下表中显示结果。首先,我们发现与表E.1中相应情况相比,参数化PDE的平均L2RE通常较高。我们认为这是因为在某些参数下,这些PDE存在一些非常高误差的困难情况。其次,我们发现PINN-NTK在参数化PDE任务上表现良好,在六个实验中取得了三个最佳结果。我们推测,解决具有不同参数的PDE需要对损失项采用不同的权重,并且PINN-NTK是一种自动平衡这些权重的强大方法。 4.3 超参数分析PINNs的性能受到超参数的强烈影响,每个变体可能都会引入自己独特的一组超参数。在这里,我们旨在通过消融研究来调查几个共享和方法特定的超参数的影响。我们考虑了批量大小和训练时期的数量。对应的结果如图2所示。我们专注于一组问题,即Burgers1d,GS,Heat2d-CG和Poisson2d-C。详细的数值结果和额外的发现在附录E.2中。 批量大小。图18的左图显示了PINNs在不同批量大小下的测试L2RE。它表明较大的批量大小提供了更优异的结果,可能是由于梯度估计精度的提高。尽管GS和Poisson2d-C在批量大小超过2048后见证到了饱和,但扩大批量大小通常会增强其余问题的结果。 训练周期 右图的图18展示了随着训练周期变化的 PINNs 的 L2RE。这反映了我们在批处理大小上观察到的趋势,我们发现周期增加导致整体误差的降低。然而,周期数量的增加也有一个饱和点。尤其是,在20k或80k周期之后,错误并没有显著下降,这表明在大约20至80周期左右 PINNs 出现了收敛。 学习率 标准 PINNs 在不同学习率和学习率计划下的性能如图3所示。我们观察到学习率对性能的影响是复杂的,最优学习率因问题而异。此外,PINN 训练往往在高学习率下,比如 ,容易导致错误峰值,而低学习率,如 ,则导致收敛速度缓慢。我们的发现表明,适中的学习率,如 或 ,或一个阶梯式衰减的学习率计划,倾向于产生更稳定的性能。 5 结论与讨论在本项工作中,我们介绍了PINNacle,一个全面的基准测试工具,提供了一个用户友好的工具箱,包含了10多种PINN方法。我们评估了这些方法在超过20个具有挑战性的PDE(偏微分方程)问题上的表现,进行了广泛的实验和超参数的剖析研究。展望未来,我们计划通过整合更多的最先进方法和更多实际问题场景来扩展这个基准测试。 我们对实验结果的分析产生了几个关键的见解。首先,对于具有复杂几何特性的问题,域分解是有益的,实验显示PINN-NTK是平衡损失权重的一个强大方法。其次,超参数的选择对PINNs的性能至关重要。选择更大的批处理大小和适当加权Adam中的损失或betas可能会显著减少误差。然而,最佳的超参数通常随PDEs变化。第三,我们认定高维和非线性问题是一个紧迫的挑战。PINNs的整体性能尚未与传统数值方法(Grossmann等人,2023年)相当。第四,从理论的角度看,训练高维或非线性问题时PINNs的损失景观的探索在很大程度上还未被开发。最后,从算法的角度来看,将神经网络的优势与数值方法(如预处理、弱形式和多重网格法)结合起来,可能是克服这里识别的挑战的一个有希望的途径(Markidis,2021年)。 |
【本文地址】
今日新闻 |
点击排行 |
|
推荐新闻 |
图片新闻 |
|
专题文章 |