圆弧中点坐标值求解（二维平面&三维空间）（3.1增加三维部分）

您所在的位置：网站首页 › 高中课本教材答案在哪里找到 › 圆弧中点坐标值求解（二维平面&三维空间）（3.1增加三维部分）

圆弧中点坐标值求解（二维平面&三维空间）（3.1增加三维部分）

2023-08-28 08:47| 来源: 网络整理| 查看: 265

圆弧中点坐标值求解二维平面

如图：假设O点坐标为（X0,Y0）,A 点坐标为（X1，Y1），C点坐标为（X，Y），从A到C的旋转角度为θ，在这里插入图片描述

复数域算法

在这里插入图片描述转自知乎：https://www.zhihu.com/question/22529500/answer/21670472

那么利用复数的算法是怎么样的呢？我们设圆心C对应的复数为 a+bi ,那么圆上任一点P对应的复数为 x0+iy0 ,P绕圆心C转过角度为α弧度后到Q,Q对应的复数为 x+yi , 根据复数乘法的意义,CQ=CP(cosα+isinα) , 即 (x-a)+(y-b)i=[(x0-a)+(y0-b)i](cosα+i*sinα)=[(x0-a)cosα-(y0-b)sinα]+[(x0-a)sinα+(y0-b)cosα]*i 根据复数相等的定义,得 x-a=(x0-a)cosα-(y0-b)sinα ,y-b=(x0-a)sinα+(y0-b)cosα , 解得： x=a+(x0-a)cosα-(y0-b)sinα , y=b+(x0-a)sinα+(y0-b)cosα . 这就是所求的坐标 .

向量算法

利用在这里插入图片描述 matlab代码求解

%二维圆弧中点坐标 syms r x0 x1 x y0 y1 y theta %eq1 = abs(x1*x-x*x0-x*x0+x0^2+y1*y-y0*y-y1*y0+y0^2) == cos(theta)*(r^2); eq1 = x1*x-x1*x0-x*x0+x0^2+y1*y-y0*y-y1*y0+y0^2 == cos(theta)*(r^2); eq2 = sqrt((x-x0)^2+(y-y0)^2) == r; [x,y] = solve(eq1,eq2,x,y); simplify(x) simplify(y)

结果：

x_1 = (x0*x1^2 - 2*x0^2*x1 + x0*y0^2 + x0*y1^2 + x0^3 - r*y0*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) + r*y1*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) - r^2*x0*cos(theta) + r^2*x1*cos(theta) - 2*x0*y0*y1)/(x0^2 - 2*x0*x1 + x1^2 + y0^2 - 2*y0*y1 + y1^2) y_1 = (x0^2*y0 + x1^2*y0 + y0*y1^2 - 2*y0^2*y1 + y0^3 + r*x0*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) - r*x1*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) - r^2*y0*cos(theta) + r^2*y1*cos(theta) - 2*x0*x1*y0)/(x0^2 - 2*x0*x1 + x1^2 + y0^2 - 2*y0*y1 + y1^2) x_2 = (x0*x1^2 - 2*x0^2*x1 + x0*y0^2 + x0*y1^2 + x0^3 + r*y0*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) - r*y1*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) - r^2*x0*cos(theta) + r^2*x1*cos(theta) - 2*x0*y0*y1)/(x0^2 - 2*x0*x1 + x1^2 + y0^2 - 2*y0*y1 + y1^2) y_2 = (x0^2*y0 + x1^2*y0 + y0*y1^2 - 2*y0^2*y1 + y0^3 - r*x0*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) + r*x1*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) - r^2*y0*cos(theta) + r^2*y1*cos(theta) - 2*x0*x1*y0)/(x0^2 - 2*x0*x1 + x1^2 + y0^2 - 2*y0*y1 + y1^2) 验算验算代码 %复数域计算验证 r = 1 ; x0 = 1; y0 = 1; x1 = 1; y1 =2 ; theta =pi/2; x_fushu = x0+(x1-x0)*cos(theta)-(y1-y0)*sin(theta) y_fushu = y0+(x1-x0)*sin(theta)+(y1-y0)*cos(theta) %验证向量计算 r = 1 ; x0 = 1; y0 = 1; x1 = 1; y1 =2 ; theta = pi/3; %顺时针算法 x_1 = (x0*x1^2 - 2*x0^2*x1 + x0*y0^2 + x0*y1^2 + x0^3 - r*y0*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) + r*y1*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) - r^2*x0*cos(theta) + r^2*x1*cos(theta) - 2*x0*y0*y1)/(x0^2 - 2*x0*x1 + x1^2 + y0^2 - 2*y0*y1 + y1^2) y_1 = (x0^2*y0 + x1^2*y0 + y0*y1^2 - 2*y0^2*y1 + y0^3 + r*x0*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) - r*x1*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) - r^2*y0*cos(theta) + r^2*y1*cos(theta) - 2*x0*x1*y0)/(x0^2 - 2*x0*x1 + x1^2 + y0^2 - 2*y0*y1 + y1^2) %逆时针算法 x_2 = (x0*x1^2 - 2*x0^2*x1 + x0*y0^2 + x0*y1^2 + x0^3 + r*y0*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) - r*y1*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) - r^2*x0*cos(theta) + r^2*x1*cos(theta) - 2*x0*y0*y1)/(x0^2 - 2*x0*x1 + x1^2 + y0^2 - 2*y0*y1 + y1^2) y_2 = (x0^2*y0 + x1^2*y0 + y0*y1^2 - 2*y0^2*y1 + y0^3 - r*x0*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) + r*x1*(x0^2 - 2*y0*y1 - r^2*cos(theta)^2 - 2*x0*x1 + x1^2 + y0^2 + y1^2)^(1/2) - r^2*y0*cos(theta) + r^2*y1*cos(theta) - 2*x0*x1*y0)/(x0^2 - 2*x0*x1 + x1^2 + y0^2 - 2*y0*y1 + y1^2) function Result = ThreePoint2Circle(P1, P2, P3) %% 求圆心和半径 x1 = P1(1); x2 = P2(1); x3 = P3(1); y1 = P1(2); y2 = P2(2); y3 = P3(2); z1 = x2^2 + y2^2 - x1^2 - y1^2; z2 = x3^2 + y3^2 - x1^2 - y1^2; z3 = x3^2 + y3^2 - x2^2 - y2^2; A = [(x2-x1), (y2-y1); (x3-x1), (y3-y1); (x3-x2), (y3-y2)]; B = 0.5*[z1; z2; z3]; P0 = (A'*A)\A'*B; R1 = sqrt( (P0(1) - P1(1))^2 + (P0(2) - P1(2))^2 ); R2 = sqrt( (P0(1) - P2(1))^2 + (P0(2) - P2(2))^2 ); R3 = sqrt( (P0(1) - P3(1))^2 + (P0(2) - P3(2))^2 ); R = (R1 + R2 + R3)/3; %% 绘制圆 theta = (0:pi/360:2*pi)'; Result = zeros(size(theta,1),4); for i = 1: size(theta,1) Result(i,1) = i; Result(i,2) = theta(i); Result(i,3) = P0(1) + R*cos(theta(i)); Result(i,4) = P0(2) + R*sin(theta(i)); end figure(); plot(Result(:,3),Result(:,4),'b-'); hold on; grid on; xlabel('x');ylabel('y'); axis equal; end 验算过程

分别以旋转pi/3和pi/2，以（1，2）点开始

①旋转±pi/2，（1，2）点开始 1）复数域算法结果旋转+pi/2 在这里插入图片描述 C点为（0，1）结论：逆时针旋转，符合条件 ——同理旋转 -pi/2，（1，2）点出发

C（2，1）在这里插入图片描述 2）向量算法结果旋转+pi/2 C点为（2，1）或者（0，1）旋转 -pi/2 C点为（2，1）或者（0，1）

同旋转+pi/2一致

**小结：两种方式旋转±pi/2，其最终结果一致，但向量法由于直接去掉绝对值的原因，直接生成两个数值

②旋转±pi/3，（1，2）点开始** 1）复数域算法结果旋转+pi/3 在这里插入图片描述 C点坐标（0.1340，1.5000）结论：逆时针旋转，符合pi/3条件 ——同理旋转 -pi/3，（1，2）点出发 C点坐标（1.8660，1.5000） 2）向量算法结果旋转+pi/3 旋转-pi/3 同旋转+pi/3结果一致

小结：两种方式旋转±pi/3，其最终结果一致，但向量法由于直接去掉绝对值的原因，直接生成两个数值

增加验证：从（1.446，1.895）出发，旋转pi/5.求最终结果？ ①复数域算法在这里插入图片描述 C（0.8348，1.9862） ②向量算法

在这里插入图片描述 C点为：（1.8869，1.4620）或（0.8348，1.9862）

在这里插入图片描述小结：两种方式旋转±pi/3，其最终结果一致，且，向量法中第二个值恒定为逆时针解，第一个值为顺时针解。

验算结论

为了方便分析结果，列表确认在这里插入图片描述

三维空间

在这里插入图片描述

向量算法算法思路

如果按照二维空间的算法方法去描述三维坐标系的下的关系，则有：在这里插入图片描述从理论角度上考虑，可求得其参数解

验证 %三维圆弧中点坐标 clear syms r x0 x1 x y0 y1 y z0 z1 z theta a b c %eq1 = abs(x1*x-x*x0-x*x0+x0^2+y1*y-y0*y-y1*y0+y0^2) == cos(theta)*(r^2); eq1 = x1*x-x1*x0-x*x0+x0^2+y1*y-y0*y-y1*y0+y0^2+z1*z-z0*z-z1*z0+z0^2 == cos(theta)*(r^2); eq2 = sqrt((x-x0)^2+(y-y0)^2+(z-z0)^2) == r; eq3 = x*a-x0*a+y*b-y0*b+z*c-z0*c == 0; [x,y,z] = solve(eq1,eq2,eq3,x,y,z); x_s = simplify(x) y_s = simplify(y) z_s = simplify(z)

计算结果极为复杂，同时代入相关点验证时候，出现NAn无解现象，由于三维空间求解问题，导致该算法并不适用三维圆弧坐标点的求解，那么我们换个思路去思考：

~如果在三维坐标系中，任意的圆弧，可以认为是是某一点绕圆轴矢量旋转一定角度后的结果，如果只在这个面内去考虑问题，可以把三维空间问题降维为二维坐标计算，即在该圆弧平面建立三维坐标系，圆弧面所在的平面Z为0，那么在已知圆心，起始点，圆弧角度的前提下，参照上面的思维很容易就可以得到在该平面坐标系下的中点坐标值。如果能够将圆弧所在坐标系能转达基础坐标系，就可以得到在基础坐标系中的该点的值。

其实，思考这么多发现，用一句话就可以描述这个问题，就是一个空间中的点绕某旋转轴旋转一定角度后的点的坐标。

那么如何去实现并且验证它呢，我们试着称该方法为旋转坐标算法！

旋转坐标算法：在这里插入图片描述前言：关于这部分的算法思路，网上其实有很多的现成公式，我们不直接调用公式，而试着用我们二维圆弧中点的算法在结合齐次坐标旋转的原理来推导这部分内容。

已知圆轴矢量为a（ax,ay,az），起点为A（x1,y1,z1），终点点为B(x,y,z)，圆心O点坐标为（x0,y0,z0）旋转弧度为：θ，XYZ为基础坐标系，X‘Y’Z‘为圆弧面三维坐标系，X轴与OA向量同向，已知圆半径r（为了方便X‘Y’Z‘直接建在以圆心O为原点的坐标系）

推导过程：

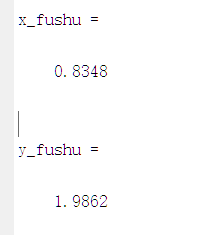在这里插入图片描述

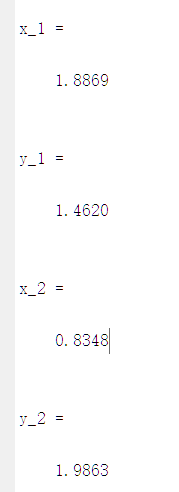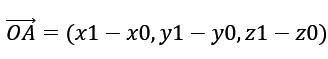
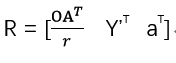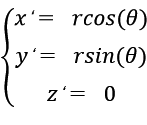
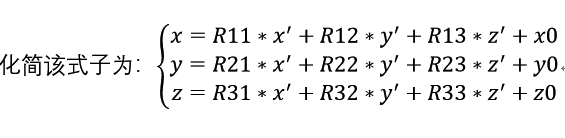y’z 在这里插入图片描述以上建立起X‘Y’Z’的坐标系，X’'Y’也就是圆弧旋转所在的平面坐标系。那么坐标系X‘Y’Z‘与坐标系XYZ的旋转变换矩阵为：首先我们求圆心在X‘Y’Z’坐标系的坐标值：根据圆角公式，不难得到：那么要求得点B在坐标系XYZ的坐标，就要将当前坐标系旋转到所求的XYZ坐标系中，利用齐次变换有：在这里插入图片描述将R的相关数值代入，可以得到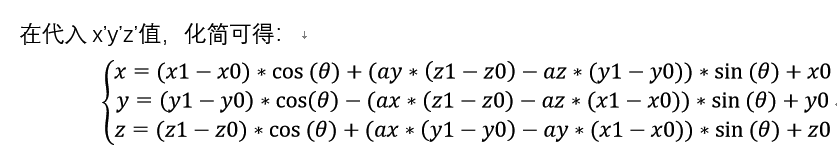：至此，利用此公式我们已经可以求得三维空间中绕某一圆轴的一段圆弧上各点坐标值。但以上公式存在一个问题，就是未将建立新建坐标系中X轴方向和所在圆弧的圆心位置圆轴矢量的垂直关系进行约束，即未锁定圆弧所在平面与圆轴矢量的垂直关系。所以在实际验证中发现，如果是垂直于三个平面的圆轴矢量，可以准确得到旋转坐标，但如果是空间任意不过原点的矢量轴时，会出现圆弧面同圆轴矢量不垂直的现象。（接下文）

【本文地址】

公司简介

联系我们