| CW测速雷达原理介绍 | 您所在的位置:网站首页 › 防空雷达工作原理图 › CW测速雷达原理介绍 |
CW测速雷达原理介绍
|
多普勒频率
固定放置的雷达发出特定频率的发射信号,遇到静止物体产生的反射信号频率并不改变,而遇到运动物体产生的反射波将会发生多普勒频移。如下图所示 根据前面的分析,CW体制雷达的回波信号是含有速度信息的正弦信号。如果速度恒定,则天线的输出信号是单一频率的正弦信号。 假设单一频率的实正弦信号可以表示为 x ( t ) = a cos ( 2 π f 0 t + θ 0 ) x\left( t \right)=a\cos \left( 2\pi {{f}_{0}}t+{{\theta }_{0}} \right) x(t)=acos(2πf0t+θ0) 其中, a a a为正弦信号的幅度, f 0 {{f}_{0}} f0为正弦信号的频率, θ 0 {{\theta }_{0}} θ0为正弦信号的初相。对上述信号进行采样,采样周期为 T s {{T}_{s}} Ts,采样频率为 f s {{f}_{s}} fs,则可以得到长度为N的序列 x ( n ) x\left( n \right) x(n) x ( n ) = a cos ( ω 0 n + θ 0 ) n = 0 , 1 , 2 , . . . , N − 1 x\left( n \right)=a\cos \left( {{\omega }_{0}}n+{{\theta }_{0}} \right)n=0,1,2,...,N-1 x(n)=acos(ω0n+θ0)n=0,1,2,...,N−1 由于 ω 0 = 2 π f 0 T s {{\omega }_{0}}=2\pi {{f}_{0}}{{T}_{s}} ω0=2πf0Ts x ( n ) x\left( n \right) x(n)的DTFT变换为 X ( e j ω ) = a 2 e j θ 0 δ ( ω − ω 0 ) + a 2 e − j θ 0 δ ( ω + ω 0 ) X\left( {{e}^{j\omega }} \right)=\frac{a}{2}{{e}^{j{{\theta }_{0}}}}\delta \left( \omega -{{\omega }_{0}} \right)+\frac{a}{2}{{e}^{-j{{\theta }_{0}}}}\delta \left( \omega +{{\omega }_{0}} \right) X(ejω)=2aejθ0δ(ω−ω0)+2ae−jθ0δ(ω+ω0) 设所采用的窗函数为矩形窗 R N ( n ) {{R}_{N}}\left( n \right) RN(n),则它的DTFT变换为 H ( e j ω ) = sin ( ω N 2 ) sin ( ω 2 ) e − j ω N − 1 2 H\left( {{e}^{j\omega }} \right)=\frac{\sin \left( \frac{\omega N}{2} \right)}{\sin \left( \frac{\omega }{2} \right)}{{e}^{-j\omega \frac{N-1}{2}}} H(ejω)=sin(2ω)sin(2ωN)e−jω2N−1 考虑到 v ( n ) = x ( n ) ∗ R N ( n ) v\left( n \right)=x\left( n \right)*{{R}_{N}}\left( n \right) v(n)=x(n)∗RN(n),根据频域卷积定理,时域的乘积对应于频域的卷积,所以 v ( n ) v\left( n \right) v(n)的DTFT变换为 V ( e j ω ) = a 2 sin [ ( ω − ω 0 ) N 2 ] sin ( ω − ω 0 ) 2 e − j ( ω − ω 0 ) N − 1 2 + j θ 0 + a 2 sin [ ( ω + ω 0 ) N 2 ] sin ( ω + ω 0 ) 2 e − j ( ω + ω 0 ) N − 1 2 − j θ 0 \begin{aligned} & V({{e}^{j\omega }})=\frac{a}{2}\frac{\sin \left[ \frac{\left( \omega -{{\omega }_{0}} \right)N}{2} \right]}{\sin \frac{\left( \omega -{{\omega }_{0}} \right)}{2}}{{e}^{-j\left( \omega -{{\omega }_{0}} \right)\frac{N-1}{2}\text{+}j{{\theta }_{0}}}} \\ & +\frac{a}{2}\frac{\sin \left[ \frac{\left( \omega +{{\omega }_{0}} \right)N}{2} \right]}{\sin \frac{\left( \omega +{{\omega }_{0}} \right)}{2}}{{e}^{-j\left( \omega +{{\omega }_{0}} \right)\frac{N-1}{2}-j{{\theta }_{0}}}} \\ \end{aligned} V(ejω)=2asin2(ω−ω0)sin[2(ω−ω0)N]e−j(ω−ω0)2N−1+jθ0+2asin2(ω+ω0)sin[2(ω+ω0)N]e−j(ω+ω0)2N−1−jθ0 考虑到 v ( k ) v\left( k \right) v(k)是 v ( e j ω ) v\left( {{e}^{j\omega }} \right) v(ejω)的频域离散化表示,因此将 v ( e j ω ) v\left( {{e}^{j\omega }} \right) v(ejω)中的 ω \omega ω用离散量 2 π N k \frac{2\pi }{N}k N2πk代入,即得到 v ( k ) v\left( k \right) v(k)表达式,考虑到 v ( k ) v\left( k \right) v(k)的对称性,只保留前半部分的表达式为 V ( k ) = a 2 sin [ ( 2 π N k − ω 0 ) N 2 ] sin ( 2 π N k − ω 0 ) 2 e − j ( 2 π N k − ω 0 ) N − 1 2 + j θ 0 V(k)=\frac{a}{2}\frac{\sin \left[ \frac{\left( \frac{2\pi }{N}k-{{\omega }_{0}} \right)N}{2} \right]}{\sin \frac{\left( \frac{2\pi }{N}k-{{\omega }_{0}} \right)}{2}}{{e}^{-j\left( \frac{2\pi }{N}k-{{\omega }_{0}} \right)\frac{N-1}{2}\text{+}j{{\theta }_{0}}}} V(k)=2asin2(N2πk−ω0)sin[2(N2πk−ω0)N]e−j(N2πk−ω0)2N−1+jθ0 V ( k ) V\left( k \right) V(k)的模为 ∣ V ( k ) ∣ = a 2 ∣ sin [ π ( k − f 0 N / f s ) ] sin π ( k − f 0 N / f s ) N ∣ \left| V(k) \right|=\frac{a}{2}\left| \frac{\sin \left[ \pi \left( k-{{f}_{0}}N/{{f}_{s}} \right) \right]}{\sin \frac{\pi \left( k-{{f}_{0}}N/{{f}_{s}} \right)}{N}} \right| ∣V(k)∣=2a∣∣∣∣∣sinNπ(k−f0N/fs)sin[π(k−f0N/fs)]∣∣∣∣∣ 设 V ( k ) V\left( k \right) V(k)中幅值最大的样本点的索引为 k 0 {{k}_{0}} k0,对应的幅值记为 A 1 {{A}_{1}} A1 A 1 = ∣ V ( k 0 ) ∣ = a 2 ∣ sin [ π ( k 0 − f 0 N / f s ) ] sin π ( k 0 − f 0 N / f s ) N ∣ {{A}_{1}}=\left| V({{k}_{0}}) \right|=\frac{a}{2}\left| \frac{\sin \left[ \pi \left( {{k}_{0}}-{{f}_{0}}N/{{f}_{s}} \right) \right]}{\sin \frac{\pi \left( {{k}_{0}}-{{f}_{0}}N/{{f}_{s}} \right)}{N}} \right| A1=∣V(k0)∣=2a∣∣∣∣∣sinNπ(k0−f0N/fs)sin[π(k0−f0N/fs)]∣∣∣∣∣ 令 δ = ( k 0 − f 0 N / f s ) = ( k 0 − f 0 f s N ) = ( k 0 − f 0 Δ f ) \delta =\left( {{k}_{0}}-{{f}_{0}}N/{{f}_{s}} \right)=\left( {{k}_{0}}-\frac{{{f}_{0}}}{\frac{{{f}_{s}}}{N}} \right)=\left( {{k}_{0}}-\frac{{{f}_{0}}}{\Delta f} \right) δ=(k0−f0N/fs)=(k0−Nfsf0)=(k0−Δff0) 则 − 0.5 < δ < 0.5 -0.5{k}_{2}} k2, k 2 = k 0 ± 1 {{k}_{2}}={{k}_{0}}\pm 1 k2=k0±1,对应的幅值记为 A 2 {{A}_{2}} A2 A 2 = ∣ V ( k 2 ) ∣ = a 2 ∣ sin [ π ( k 2 − f 0 N / f s ) ] sin π ( k 2 − f 0 N / f s ) N ∣ {{A}_{2}}=\left| V({{k}_{2}}) \right|=\frac{a}{2}\left| \frac{\sin \left[ \pi \left( {{k}_{2}}-{{f}_{0}}N/{{f}_{s}} \right) \right]}{\sin \frac{\pi \left( {{k}_{2}}-{{f}_{0}}N/{{f}_{s}} \right)}{N}} \right| A2=∣V(k2)∣=2a∣∣∣∣∣sinNπ(k2−f0N/fs)sin[π(k2−f0N/fs)]∣∣∣∣∣ 当 δ < 0 \delta {A}_{2}}=\left| V({{k}_{2}}) \right|=\frac{a}{2}\left| \frac{\sin \left[ \pi \left( {{k}_{0}}\text{+}1-{{f}_{0}}N/{{f}_{s}} \right) \right]}{\sin \frac{\pi \left( {{k}_{0}}\text{+}1-{{f}_{0}}N/{{f}_{s}} \right)}{N}} \right| \\ & \text{=}\frac{a}{2}\left| \frac{\sin \left[ \pi \delta +\pi \right]}{\sin \frac{\pi \delta +\pi }{N}} \right|=\frac{aN}{2\pi }\left| \frac{\sin \pi \delta }{1+\delta } \right| \\ \end{aligned} A2=∣V(k2)∣=2a∣∣∣∣∣sinNπ(k0+1−f0N/fs)sin[π(k0+1−f0N/fs)]∣∣∣∣∣=2a∣∣∣∣∣sinNπδ+πsin[πδ+π]∣∣∣∣∣=2πaN∣∣∣∣1+δsinπδ∣∣∣∣ 当 δ > 0 \delta >0 δ>0的时候, k 2 = k 0 − 1 {{k}_{2}}={{k}_{0}}-1 k2=k0−1,代入得到 A 2 = ∣ V ( k 2 ) ∣ = a 2 ∣ sin [ π ( k 0 − 1 − f 0 N / f s ) ] sin π ( k 0 − 1 − f 0 N / f s ) N ∣ = a 2 ∣ sin [ π δ − π ] sin π δ − π N ∣ = a N 2 π ∣ sin π δ 1 − δ ∣ \begin{aligned} & {{A}_{2}}=\left| V({{k}_{2}}) \right|=\frac{a}{2}\left| \frac{\sin \left[ \pi \left( {{k}_{0}}-1-{{f}_{0}}N/{{f}_{s}} \right) \right]}{\sin \frac{\pi \left( {{k}_{0}}-1-{{f}_{0}}N/{{f}_{s}} \right)}{N}} \right| \\ & \text{=}\frac{a}{2}\left| \frac{\sin \left[ \pi \delta -\pi \right]}{\sin \frac{\pi \delta -\pi }{N}} \right|=\frac{aN}{2\pi }\left| \frac{\sin \pi \delta }{1-\delta } \right| \\ \end{aligned} A2=∣V(k2)∣=2a∣∣∣∣∣sinNπ(k0−1−f0N/fs)sin[π(k0−1−f0N/fs)]∣∣∣∣∣=2a∣∣∣∣∣sinNπδ−πsin[πδ−π]∣∣∣∣∣=2πaN∣∣∣∣1−δsinπδ∣∣∣∣ 综上,次大值的表达式为 A 2 = ∣ X ( k 2 ) ∣ = N a ∣ sin ( π δ ) ∣ 2 π ( 1 − ∣ δ ∣ ) {{A}_{2}}=\left| X\left( {{k}_{2}} \right) \right|=\frac{Na\left| \sin \left( \pi \delta \right) \right|}{2\pi \left( 1-\left| \delta \right| \right)} A2=∣X(k2)∣=2π(1−∣δ∣)Na∣sin(πδ)∣ 次大值和最大值的比值为 α = A 2 A 1 = ∣ δ ∣ 1 − ∣ δ ∣ \alpha =\frac{{{A}_{2}}}{{{A}_{1}}}=\frac{\left| \delta \right|}{1-\left| \delta \right|} α=A1A2=1−∣δ∣∣δ∣ 则可以得到 ∣ δ ∣ = α 1 + α = A 2 A 1 + A 2 \left| \delta \right|=\frac{\alpha }{1+\alpha }=\frac{{{A}_{2}}}{{{A}_{1}}+{{A}_{2}}} ∣δ∣=1+αα=A1+A2A2 根据 δ \delta δ值可对离散频谱得到的 f 0 {{f}_{0}} f0的估计值插值从而得到更精细的频率估计值 f 0 ∧ = ( k 0 ± ∣ δ ∣ ) N T s \overset{\wedge }{\mathop{{{f}_{0}}}}\,=\frac{({{k}_{0}}\pm \left| \delta \right|)}{N{{T}_{s}}} f0∧=NTs(k0±∣δ∣) 式中符号根据 k 2 {{k}_{2}} k2的位置确定,若 k 2 = k 0 + 1 {{k}_{2}}={{k}_{0}}+1 k2=k0+1取加号,反之取减号。 以上就是CW雷达测速的原理。 |
【本文地址】
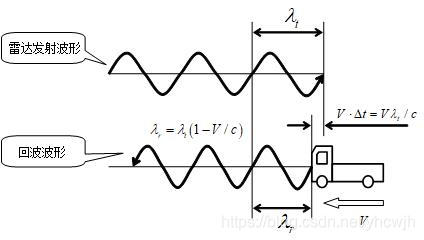 图中,
V
V
V表示汽车行驶速度,
c
c
c表示电磁波传播速度,
λ
t
{{\lambda }_{t}}
λt表示雷达发射波的波长,
λ
r
{{\lambda }_{r}}
λr表示回波信号的波长。 将雷达的接收信号与回波信号进行混频,产生低频信号,即为多普勒信号。 假设雷达发射信号表示为
s
t
(
t
)
=
A
cos
(
ω
0
t
+
φ
)
{{s}_{t}}\left( t \right)=A\cos \left( {{\omega }_{0}}t+\varphi \right)
st(t)=Acos(ω0t+φ) 式中,
ω
0
{{\omega }_{0}}
ω0为发射角频率,
φ
\varphi
φ为初相,
A
A
A为振幅。 回波信号
s
r
(
t
)
{{s}_{r}}\left( t \right)
sr(t)可以表示为
s
r
(
t
)
=
k
s
t
(
t
−
t
r
)
=
k
A
cos
[
w
0
(
t
−
t
r
)
+
φ
]
{{s}_{r}}\left( t \right)=k{{s}_{t}}\left( t-{{t}_{r}} \right)=kA\cos \left[ {{w}_{0}}\left( t-{{t}_{r}} \right)+\varphi \right]
sr(t)=kst(t−tr)=kAcos[w0(t−tr)+φ] 式中,
t
r
=
2
R
/
c
{{t}_{r}}=2R/c
tr=2R/c,表示回波信号滞后于发射信号的时间,
k
k
k为回波的衰减系数。 如果目标固定不动,则距离
R
R
R为常数。回波与发射信号之间有固定的相位差
ω
0
t
r
=
2
π
f
0
⋅
2
R
/
c
=
(
2
π
/
λ
)
2
R
{{\omega }_{0}}{{t}_{r}}=2\pi {{f}_{0}}\cdot 2R/c=\left( 2\pi /\lambda \right)2R
ω0tr=2πf0⋅2R/c=(2π/λ)2R 当目标与雷达之间存在相对运动,则距离
R
R
R随时间变化。设目标以匀速相对雷达运动,则在时间
t
t
t时刻,目标与雷达间的距离
R
(
t
)
R\left( t \right)
R(t)为
R
(
t
)
=
R
0
−
v
r
t
R\left( t \right)={{R}_{0}}-{{v}_{r}}t
R(t)=R0−vrt 上式表明,在
t
t
t时刻接收到的波形
s
r
(
t
)
{{s}_{r}}\left( t \right)
sr(t)上的点,是雷达在
t
−
t
r
t-{{t}_{r}}
t−tr时刻发射的。因为通常雷达和目标间的相对运动速度
v
r
{{v}_{r}}
vr远小于电磁波速度
c
c
c,所以时延
t
r
{{t}_{r}}
tr可以表示为
t
r
=
2
R
(
t
)
c
=
2
c
(
R
0
−
v
r
t
)
{{t}_{r}}=\frac{2R\left( t \right)}{c}=\frac{2}{c}\left( {{R}_{0}}-{{v}_{r}}t \right)
tr=c2R(t)=c2(R0−vrt) 回波信号和发射信号相比,高频相位差为
φ
=
−
ω
0
t
r
=
−
ω
0
2
c
(
R
0
−
v
r
t
)
=
−
2
π
2
λ
(
R
0
−
v
r
t
)
\varphi =-{{\omega }_{0}}{{t}_{r}}=-{{\omega }_{0}}\frac{2}{c}\left( {{R}_{0}}-{{v}_{r}}t \right)=-2\pi \frac{2}{\lambda }\left( {{R}_{0}}-{{v}_{r}}t \right)
φ=−ω0tr=−ω0c2(R0−vrt)=−2πλ2(R0−vrt) 是时间
t
t
t的函数,在径向速度
v
r
{{v}_{r}}
vr为常数时,产生频率差为
f
d
=
1
2
π
d
φ
d
t
=
2
λ
v
r
{{f}_{d}}=\frac{1}{2\pi }\frac{d\varphi }{dt}=\frac{2}{\lambda }{{v}_{r}}
fd=2π1dtdφ=λ2vr 上述公式即是多普勒频率的公式
图中,
V
V
V表示汽车行驶速度,
c
c
c表示电磁波传播速度,
λ
t
{{\lambda }_{t}}
λt表示雷达发射波的波长,
λ
r
{{\lambda }_{r}}
λr表示回波信号的波长。 将雷达的接收信号与回波信号进行混频,产生低频信号,即为多普勒信号。 假设雷达发射信号表示为
s
t
(
t
)
=
A
cos
(
ω
0
t
+
φ
)
{{s}_{t}}\left( t \right)=A\cos \left( {{\omega }_{0}}t+\varphi \right)
st(t)=Acos(ω0t+φ) 式中,
ω
0
{{\omega }_{0}}
ω0为发射角频率,
φ
\varphi
φ为初相,
A
A
A为振幅。 回波信号
s
r
(
t
)
{{s}_{r}}\left( t \right)
sr(t)可以表示为
s
r
(
t
)
=
k
s
t
(
t
−
t
r
)
=
k
A
cos
[
w
0
(
t
−
t
r
)
+
φ
]
{{s}_{r}}\left( t \right)=k{{s}_{t}}\left( t-{{t}_{r}} \right)=kA\cos \left[ {{w}_{0}}\left( t-{{t}_{r}} \right)+\varphi \right]
sr(t)=kst(t−tr)=kAcos[w0(t−tr)+φ] 式中,
t
r
=
2
R
/
c
{{t}_{r}}=2R/c
tr=2R/c,表示回波信号滞后于发射信号的时间,
k
k
k为回波的衰减系数。 如果目标固定不动,则距离
R
R
R为常数。回波与发射信号之间有固定的相位差
ω
0
t
r
=
2
π
f
0
⋅
2
R
/
c
=
(
2
π
/
λ
)
2
R
{{\omega }_{0}}{{t}_{r}}=2\pi {{f}_{0}}\cdot 2R/c=\left( 2\pi /\lambda \right)2R
ω0tr=2πf0⋅2R/c=(2π/λ)2R 当目标与雷达之间存在相对运动,则距离
R
R
R随时间变化。设目标以匀速相对雷达运动,则在时间
t
t
t时刻,目标与雷达间的距离
R
(
t
)
R\left( t \right)
R(t)为
R
(
t
)
=
R
0
−
v
r
t
R\left( t \right)={{R}_{0}}-{{v}_{r}}t
R(t)=R0−vrt 上式表明,在
t
t
t时刻接收到的波形
s
r
(
t
)
{{s}_{r}}\left( t \right)
sr(t)上的点,是雷达在
t
−
t
r
t-{{t}_{r}}
t−tr时刻发射的。因为通常雷达和目标间的相对运动速度
v
r
{{v}_{r}}
vr远小于电磁波速度
c
c
c,所以时延
t
r
{{t}_{r}}
tr可以表示为
t
r
=
2
R
(
t
)
c
=
2
c
(
R
0
−
v
r
t
)
{{t}_{r}}=\frac{2R\left( t \right)}{c}=\frac{2}{c}\left( {{R}_{0}}-{{v}_{r}}t \right)
tr=c2R(t)=c2(R0−vrt) 回波信号和发射信号相比,高频相位差为
φ
=
−
ω
0
t
r
=
−
ω
0
2
c
(
R
0
−
v
r
t
)
=
−
2
π
2
λ
(
R
0
−
v
r
t
)
\varphi =-{{\omega }_{0}}{{t}_{r}}=-{{\omega }_{0}}\frac{2}{c}\left( {{R}_{0}}-{{v}_{r}}t \right)=-2\pi \frac{2}{\lambda }\left( {{R}_{0}}-{{v}_{r}}t \right)
φ=−ω0tr=−ω0c2(R0−vrt)=−2πλ2(R0−vrt) 是时间
t
t
t的函数,在径向速度
v
r
{{v}_{r}}
vr为常数时,产生频率差为
f
d
=
1
2
π
d
φ
d
t
=
2
λ
v
r
{{f}_{d}}=\frac{1}{2\pi }\frac{d\varphi }{dt}=\frac{2}{\lambda }{{v}_{r}}
fd=2π1dtdφ=λ2vr 上述公式即是多普勒频率的公式