| 遗传算法(GA)解决TSP问题 | 您所在的位置:网站首页 › 遗传算法求解tsp问题源代码 › 遗传算法(GA)解决TSP问题 |
遗传算法(GA)解决TSP问题
|
遗传算法解决TSP问题
遗传算法 遗传算法的基本原理是通过作用于染色体上的基因寻找好的染色体来求解问题,它需要对算法所产生的每个染色体进行评价,并基于适应度值来选择染色体,使适应性好的染色体有更多的繁殖机会,在遗传算法中,通过随机方式产生若干个所求解问题的数字编码,即染色体,形成初始种群;通过适应度函数给每个个体一个数值评价,淘汰低适应度的个体,选择高适应度的个体参加遗传操作,经过遗产操作后的个体集合形成下一代新的种群,对这个新的种群进行下一轮的进化。
TSP问题 TSP问题即旅行商问题,经典的TSP可以描述为:一个商品推销员要去若干个城市推销商品,该推销员从一个城市出发,需要经过所有城市后,回到出发地。应如何选择行进路线,以使总的行程最短。从图论的角度来看,该问题实质是在一个带权完全无向图中,找一个权值最小的哈密尔顿回路。
遗传算法解决TSP问题 概念介绍: 种群 ==> 可行解集 个体 ==> 可行解 染色体 ==> 可行解的编码 基因 ==> 可行解编码的分量 基因形式 ==> 遗传编码 适应度 ==> 评价的函数值(适应度函数) 选择 ==> 选择操作 交叉 ==> 编码的交叉操作 变异 ==> 可行解编码的变异 遗传操作:就包括优选适应性强的个体的“选择”;个体间交换基因产生新个体的“交叉”;个体间的基因突变而产生新个体的“变异”。其中遗传算法是运用遗传算子来进行遗传操作的。即:选择算子、变异算子、交叉算子。
遗传算法的基本运算过程 (1)种群初始化:个体编码方法有二进制编码和实数编码,在解决TSP问题过程中个体编码方法为实数编码。对于TSP问题,实数编码为1-n的实数的随机排列,初始化的参数有种群个数M、染色体基因个数N(即城市的个数)、迭代次数C、交叉概率Pc、变异概率Pmutation。 (2)适应度函数:在TSP问题中,对于任意两个城市之间的距离D(i,j)已知,每个染色体(即n个城市的随机排列)可计算出总距离,因此可将一个随机全排列的总距离的倒数作为适应度函数,即距离越短,适应度函数越好,满足TSP要求。 (3)选择操作:采用基于适应度比例的选择策略,即适应度越好的个体被选择的概率越大,同时在选择中保存适应度最高的个体。 (4)交叉操作:对于个体,随机选择两个个体,在对应位置交换若干个基因片段,同时保证每个个体依然是1-n的随机排列,防止进入局部收敛。 例如:
对A的4 3 2进行和B的交叉时,将B的2 6 7换至A,同时将A中的6 7(B换上来但A已包含)和B中对应的数字进行交叉,6->3 7->2 (5)变异操作:对于变异操作,随机选取个体,同时随机选取个体的两个基因进行交换以实现变异操作。 产生新的群体后再次进行评估,然后再选择、交叉、变异,一直循环这几步,最终找到一个近似最优解。
遗传算法的终止条件 当最优个体的适应度达到给定的阈值 最优个体的适应度和群体适应度不再上升 迭代次数达到预设的代数时,算法终止
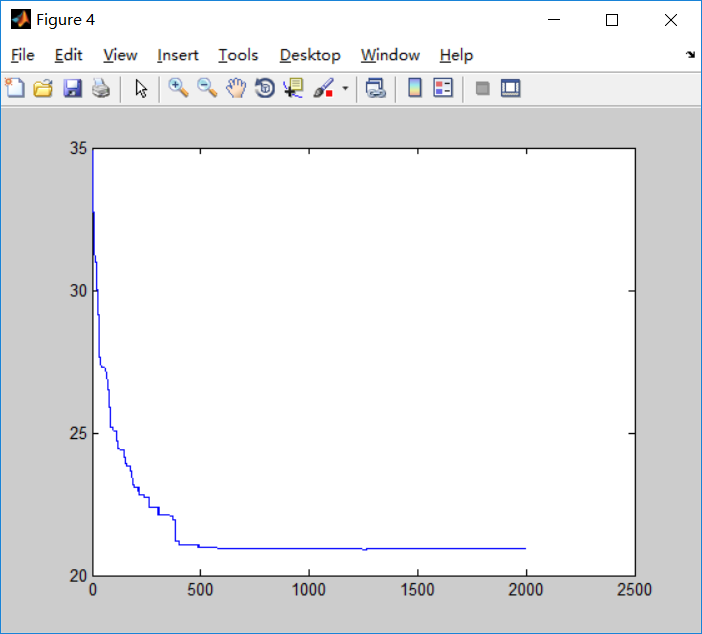
运行结果: 第一次测试
N=25; %城市的个数 M=100; %种群的个数 TER=2000; %迭代次数 Pc=0.8; %%交叉概率Pmutation=0.05; %%变异概率 迭代2000次之后运行结果并不能算是很好,整体迭代了600次左右趋于平稳,但仍有部分细微波动,运行时间相较于蚁群算法更快。
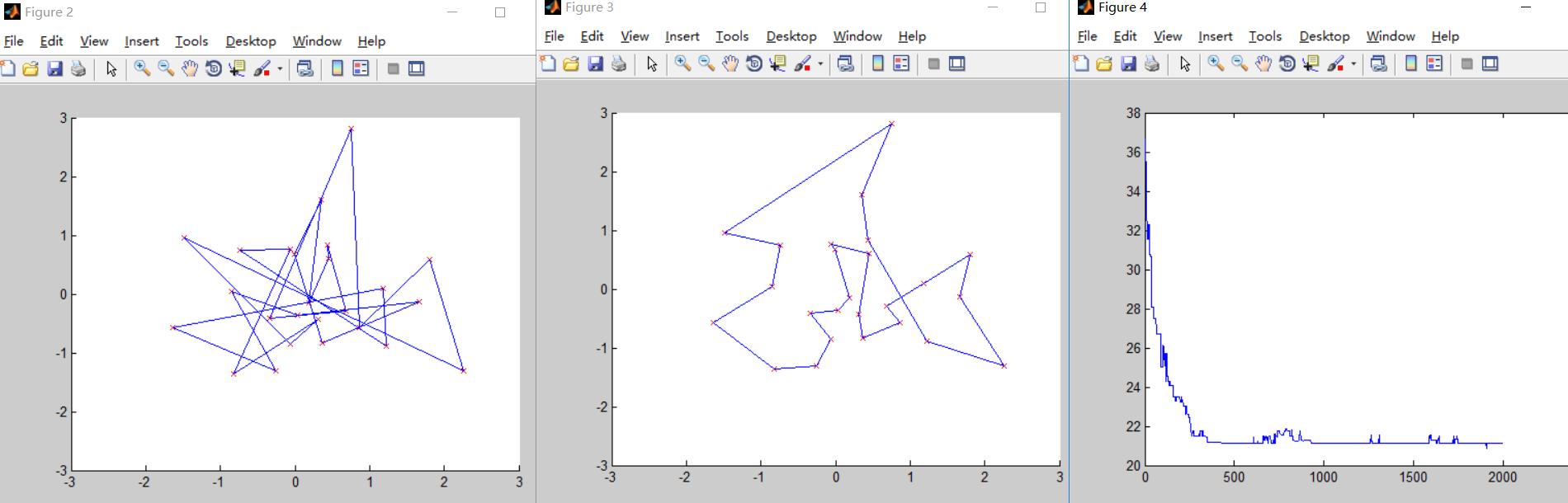
第二次测试
N=25; %城市的个数 M=100; %种群的个数 TER=2000; %迭代次数 Pc=0.95; %交叉概率Pmutation=0.1; %变异概率 提高了变异概率和交叉概率,虽然最终结果的准确性有略微提升,但是牺牲了运行时间和迭代次数,迭代次数远远大于第一次测试,可见变异概率和交叉概率过大对实验结果存在一定影响。
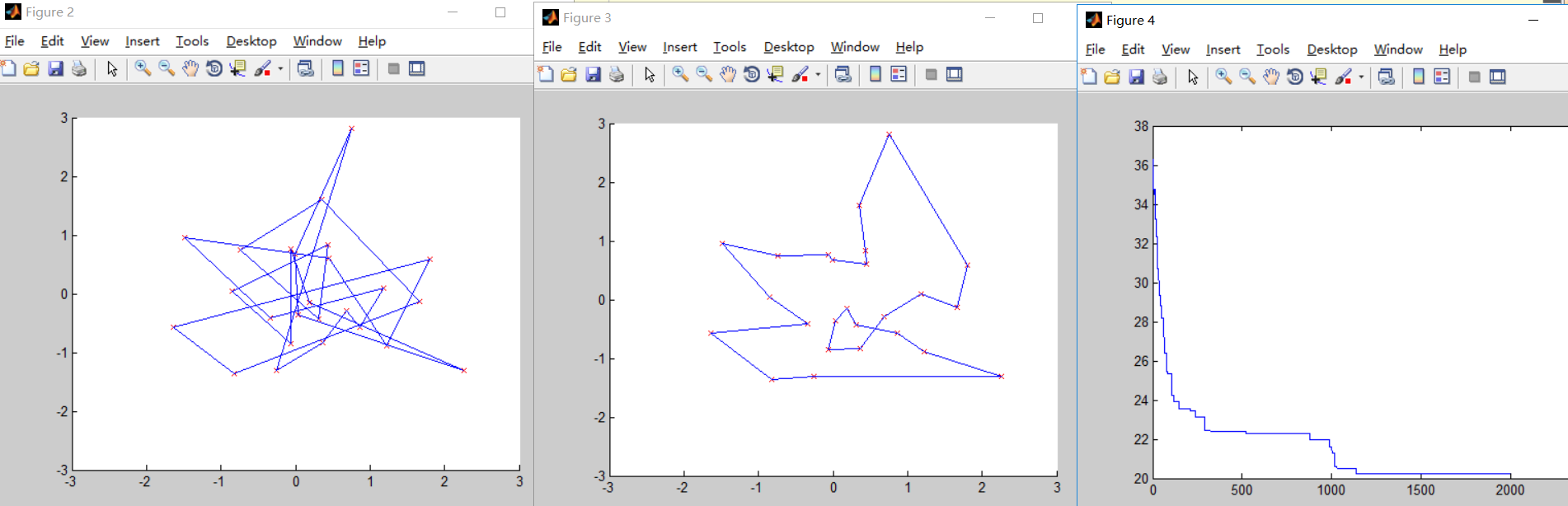
第三次测试
N=25; %城市的个数 M=100; %种群的个数 TER=2000; %迭代次数 Pc=0.4; %交叉概率Pmutation=0.01; %变异概率 结合第二次测试可以看出,交叉概率和变异概率不能过大,否则波动较大,迭代时间较长,同样也不能过小,否则很难找到最优解
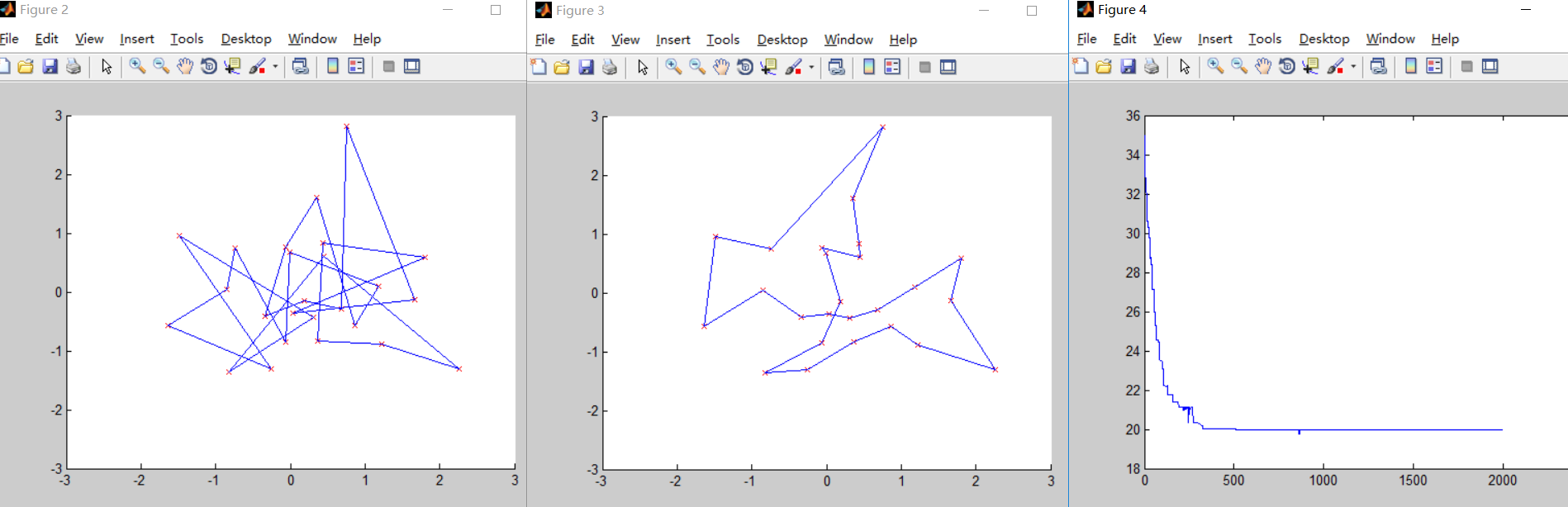
第四次测试
N=25; %城市的个数 M=200; %种群的个数 TER=2000; %迭代次数 Pc=0.8; %交叉概率Pmutation=0.05; %变异概率 种群的个数增加成原来的一倍后,运行的结果更加精确,但是相应的迭代次数会增加,时间成本增加
第五次测试
N=25; %城市的个数 M=500; %种群的个数 TER=2000; %迭代次数 Pc=0.8; %交叉概率Pmutation=0.05; %变异概率 可以发现当种群个数增加更多之后,迭代次数大幅减少,但是运行的时间与第四次测试相比增加了近20秒,时间成本增加了很多,所以种群个数同样不应该过大。
总结 对同一个TSP问题,分析种群规模、交叉概率和变异概率对算法结果的影响: (1)改变种群个数后的影响-->种群个数增大,算法结果的精确度会有一定的提升,但是运行时间相较之前更久了。
(2)改变交叉概率后的影响-->交叉概率过低将很难得不到最优解,交叉概率越高则平均适应度越好,但是也不能过高,否则会影响迭代时间。
(3)改变变异概率概率后的影响-->变异概率过高或者过低都会影响运行得到最优解
(4)遗传算法得到的结果的精确度会受到交叉概率、变异概率、迭代次数的影响:迭代次数越大,变异概率越小,则遗传算法的精确度越高。执行时间随着迭代次数的增加而增加。当交叉概率为0.8,变异概率为0.5,结果相对来说会稍微好一些,整体来说运用遗传算法来求解TSP问题的速度要比用蚁群算法来解决TSP问题快的多,所以适当将迭代次数增加一些也没有什么影响。
代码 %main clear; clc; %%%%%%%%%%%%%%%输入参数%%%%%%%% N=25; %%城市的个数 M=100; %%种群的个数 ITER=2000; %%迭代次数 %C_old=C; m=2; %%适应值归一化淘汰加速指数 Pc=0.8; %%交叉概率 Pmutation=0.05; %%变异概率 %%生成城市的坐标 pos=[-0.0596300734351115 -0.851297433985992; 0.438398458335735 0.841724248850041; -0.251804207069105 -1.30744728793171; 1.17790692164388 0.0952195708913433; 1.66427009988301 -0.133382476901910; -0.337308956003599 -0.407225198007313; 0.311862707690034 -0.431724333072457; 0.182396732713558 -0.157788333124223; 0.0378390295101906 -0.367920724129644; -0.853709951356673 0.0363449796675028; -1.64191242274810 -0.565028275383299; -0.821481309108439 -1.36166562718530; -0.0666502703726364 0.756667745411741; 2.25931856568426 -1.30140683361980; 0.759098750479421 2.81038357991309; -0.00925105144207478 0.672464995693229; 0.862239245550680 -0.576524359942781; -0.742512628202077 0.740723643506810; 0.371005938734921 -0.835740815137822; 0.677683424862960 -0.284758907693345; -1.48234180628974 0.955162776644004; 0.452806831664590 0.608019647737753; 1.22196689592397 -0.878318328597688; 0.352173262723895 1.60512181080303; 1.80729484625293 0.593061432086341 ]; %%生成城市之间距离矩阵 D=zeros(N,N); for i=1:N for j=i+1:N dis=(pos(i,1)-pos(j,1)).^2+(pos(i,2)-pos(j,2)).^2; D(i,j)=dis^(0.5); D(j,i)=D(i,j); end end %%生成初始群体 popm=zeros(M,N); for i=1:M popm(i,:)=randperm(N);%随机排列,比如[2 4 5 6 1 3] end %%随机选择一个种群 R=popm(1,:); figure(1); scatter(pos(:,1),pos(:,2),'rx');%画出所有城市坐标 axis([-3 3 -3 3]); figure(2); plot_route(pos,R); %%画出初始种群对应各城市之间的连线 axis([-3 3 -3 3]); %%初始化种群及其适应函数 fitness=zeros(M,1); len=zeros(M,1); for i=1:M%计算每个染色体对应的总长度 len(i,1)=myLength(D,popm(i,:)); end maxlen=max(len);%最大回路 minlen=min(len);%最小回路 fitness=fit(len,m,maxlen,minlen); rr=find(len==minlen);%找到最小值的下标,赋值为rr R=popm(rr(1,1),:);%提取该染色体,赋值为R for i=1:N fprintf('%d ',R(i));%把R顺序打印出来 end fprintf('\n'); fitness=fitness/sum(fitness); distance_min=zeros(ITER+1,1); %%各次迭代的最小的种群的路径总长 nn=M; iter=0; while iter10 W=ceil(L/10)+8; else W=floor(L/10)+8; end %%W为需要交叉的位数 p=(L-W+1);%随机产生一个交叉位置 %fprintf('p=%d ',p);%交叉位置 for i=1:W x=find(A==B(1,p+i-1)); y=find(B==A(1,p+i-1)); [A(1,p+i-1),B(1,p+i-1)]=exchange(A(1,p+i-1),B(1,p+i-1)); [A(1,x),B(1,y)]=exchange(A(1,x),B(1,y)); end end %对调函数 exchange.m function [x,y]=exchange(x,y) temp=x; x=y; y=temp; end %适应度函数fit.m,每次迭代都要计算每个染色体在本种群内部的优先级别,类似归一化参数。越大约好! function fitness=fit(len,m,maxlen,minlen) fitness=len; for i=1:length(len) fitness(i,1)=(1-(len(i,1)-minlen)/(maxlen-minlen+0.0001)).^m; end %变异函数 Mutation.m function a=Mutation(A) index1=0;index2=0; nnper=randperm(size(A,2)); index1=nnper(1); index2=nnper(2); %fprintf('index1=%d ',index1); %fprintf('index2=%d ',index2); temp=0; temp=A(index1); A(index1)=A(index2); A(index2)=temp; a=A; end %染色体的路程代价函数 mylength.m function len=myLength(D,p)%p是一个排列 [N,NN]=size(D); len=D(p(1,N),p(1,1)); for i=1:(N-1) len=len+D(p(1,i),p(1,i+1)); end end %连点画图函数 plot_route.m function plot_route(a,R) scatter(a(:,1),a(:,2),'rx'); hold on; plot([a(R(1),1),a(R(length(R)),1)],[a(R(1),2),a(R(length(R)),2)]); hold on; for i=2:length(R) x0=a(R(i-1),1); y0=a(R(i-1),2); x1=a(R(i),1); y1=a(R(i),2); xx=[x0,x1]; yy=[y0,y1]; plot(xx,yy); hold on; end end
|
【本文地址】