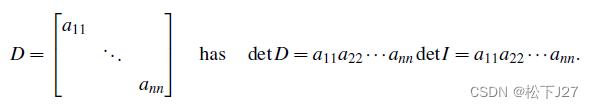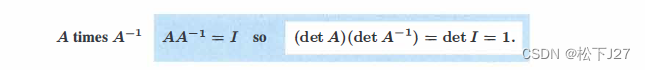线性代数

        矩阵的行列式(Determinant)既可以表示成“det A”,也可以用“|A|”来表示。矩阵的行列式是一个数，这个数能够反应一些关于矩阵的信息。注意，行列式只对方阵有效。

若矩阵A为：

则A的行列式为：

性质1： 单位矩阵的行列式等于1

性质2：行与行之间的交换会改变det的正负号

以2x2单位矩阵为例:

换行后：

        此外，如果进行过多次交换。行交换的次数为偶数，则det的行列式的符号不变。如果为奇数，则仍需改变det的符号。 

性质3(分成两个知识点)：在其他行不变的情况下，行列式是其中一行的线性函数

3A，如果矩阵中的某一行的每个元素都成一个系数t，则他的行列式也要相应的乘以t。

对左边而言，矩阵的行列式为tad-tbc。对等式右边而言，行列式为t(ad-bc)=tab-tbc，左右相等。 

3B，如果矩阵中的某一行的每个元素都加上一个系数，则新矩阵的行列式等于：

对左边而言，行列式的值为(a+a')d-(b+b')c=ad+a'd-bc-b'c。对等式右边而言，(ad-bc)+(a'd-b'c)=ad+a'd-bc-b'c，左右相等。

        以上三条最最重要的性质对所有nxn矩阵都是适用的，虽然我这里为了方便只拿2x2矩阵矩阵，可自行证明。更重要的是，后面提到的所有性质都是基于这三个性质的，或者说都可以用这三个性质来证明，而无需套用nxn行列式的计算方法去证明。

IMPORTANT！！！：下列所有其他性质的证明都不是用文中最开始提到了2x2矩阵行列式的算式去证明的，而是用前面列出来的三个重要性质以及他们的一些衍生性质证明的（唯独这三个重要性质的证明需要用到2x2矩阵行列式的算式）

性质4：如果矩阵A中有两行相等，则A的行列式为0

证明：

        假设矩阵A为上面的矩阵，则对A的相等的两行进行行交换后，A还是A，不变。这就说如果原矩阵A的行列式为D，则对A进行行交换后的行列式还应该是D。但是，按照前面提到的性质2，对矩阵进行奇数次行交换后，行列式的符号要改变。因此，A的行列式因改为-D。但对A进行行交换后还是A，因此，他的行列式应该还是D。等式-D=D只在D=0时才满足，因此，如果A中有两行相当，则A的行列式必为0。

性质5：对矩阵进行高斯消元不会改变矩阵的行列式

换句话就是矩阵的中的一行减去另一行乘以一个系数后，行列式的值不变：

证明：

        首先根据性质3B，可以把等式的右边改写成两个行列式的和：

然后根据性质3A，可把上式中的系数提到外面去：

最后因为其中有一个矩阵中有两行相等，根据性质4他的行列式为0，最终得到和原矩阵的行列式相等：

        这也就是说，如果对一个矩阵A进行高斯消元后得到U，则A的行列式和U的行列式相等。又因为高斯消元的过程中可能需要进行行交换，则总有：

性质6：如果矩阵存在全0行，则矩阵的行列式为0

证明：

        首先，根据性质5。让矩阵的第二行减去第一行乘以系数-1后，得到的新矩阵两行都是a b，且行列式的值不变。然后再根据性质4，矩阵中有两行相等，则行列式的值为0。

性质7：如果A是三角阵，则矩阵A的行列式等于主对角线上所有元素的乘积

证明：

        假设A为上三角矩阵，则可对A使用高斯消元，消除主对角线上的所有元素。根据性质5，行列式的值不发生改变。

        接下来，根据性质3a,矩阵的行列式对于其中一行而言是线性的。因此，可以依次提出每行主对角线上的系数，得到：

        最后，根据性质1，单位矩阵的行列式等于1。最终得到矩阵A的行列式为：

性质8：如果A为奇异矩阵，则A的行列式为0。如果A为非奇异矩阵，则A的行列式不等于0。

证明：

        对任意方阵A进行高斯消元得到U，根据性质5，不改变行列式的值。如果A为奇异矩阵，则U必有全0行。根据性质6，如果矩阵中有全0行，则矩阵的行列式为0。因此，A为奇异矩阵时，A的行列式为0。

        同理，如果方阵A为非奇异矩阵，则消元后的U必为三角阵，且主对角线上没有0。再根据性质7，三角阵的行列式等于主对角线上所有元素的乘积。进而得到：

因此，U的行列式必不等于0。推出，若A为非奇异矩阵，则A的行列式不为0。

性质9：AB的行列式等于A的行列式乘以B的行列式：|AB|=|A||B|

证明：

假设A，B都是非奇异矩阵。对矩阵A消元(先消去主元列下的所有元素化A为U，再消去主元列上的所有元素化U为D)得到对角阵D，且不改变A的行列式的绝对值。这样一来上式就变成了：

注意，如果消元的过程中发生过符号的改变，最终等式左边和右边的改变都是一样的。

对等式右边而言(一定要注意这里的乘法顺序。D左乘B，是以D的行为权重对B的各行进行的操作)：

在求DB的行列式时，可根据性质3A把所有系数都提出来的，得到：

对于等式右边，可以直接根据性质7得到和上面一样的答案。

这是一条非常有用的性质。首先，他可以用来计算逆矩阵的行列式。

已知矩阵A，那么根据性质9，我们无需求出A的逆矩阵，就能知道逆矩阵的行列式。

 其次，它可以用来计算矩阵的n次方的行列式：

 性质10：矩阵A的转置的行列式等于A的行列式

证明：

分别对左右两边做LU分解得到：

根据性质9，可得：

L为三角阵，且L的主对角线上都是1，因此：

（注：如果消元过程中出现过换行，则可能会是-1。但就算是改变符号，也是等式左右两边同时改变的，不影响证明）

最终得到：

证毕！

性质10的重要之处在于，前面我所讨论的所有的矩阵性质都是基于矩阵的行讨论的。现在我们知道了如果对矩阵进行转置不会改变矩阵的行列式，就相当于是可以把前面所有适用于矩阵行的性质同样应用到对矩阵的列上。

（全文完）

作者 --- 松下J27 

参考文献(鸣谢)：

1，Introduction to Linear Algebra，Fifth Edition - Gilbert Strang

2，麻省理工Gilbert Strang教授线代大师-线性代数（全）_哔哩哔哩_bilibili

（配图与本文无关） 

版权声明：文中的部分图片，文字或者其他素材，可能来自很多不同的网站和说明，在此没法一一列出，如有侵权，请告知，立即删除。欢迎大家转载，但是，如果有人引用或者COPY我的文章，必须在你的文章中注明你所使用的图片或者文字来自于我的文章，否则，侵权必究。 ----松下J27