希尔方程

1878年，希尔在研究日、地、月系统中月球的运动时，建立了一组相对运动方程。它是一组非线性微分方程，希尔没有对方程组线性化，而是以时间幂级数的形式给出了一组运动解。1960年，W. H. Clohessy和R. S. Wiltshire研究交会对接问题时采用了该组方程，并进行了线性化。因此，该方程称为希尔方程（Hill Equation），也称为Clohessy - Wiltshire方程（简称C-W方程）： \[\left\{ {\begin{array}{*{20}{l}} { {\ddot x}}+{2 \omega }{\dot y} = f_x\\ { {\ddot y}}-{2 \omega }{\dot x} -{3\omega^{2}}{y}= f_y\\ { {\ddot z}}+{\omega^{2}}{z} = f_z\\ \end{array}} \right.\]

以目标航天器的轨道（运动）坐标系$Oxyz$为参考，研究追赶航天器相对它的运动。轨道（运动）坐标系$Oxyz$的$Oy$轴沿地球半径方向，$Ox$轴与$Oy$轴垂直指向飞行的前方，$Oxy$在轨道平面内，$Oz$轴与前两者构成右旋正交系。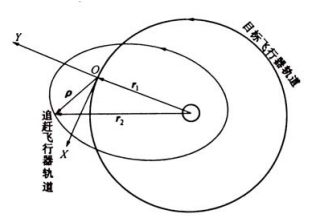

目标航天器的运动方程式是 \[{\boldsymbol{\ddot r_1}} +{\frac{\mu}{r_1^3}}{\boldsymbol{r_1}}= 0\] 追赶航天器的运动方程式是 \[{\boldsymbol{\ddot r_2}} +{\frac{\mu}{r_2^3}}{\boldsymbol{r_2}}= \boldsymbol{f}\] 其中，$\boldsymbol{f}$是追赶航天器单位质量的上作用力，使其可控。 追赶航天器相对目标航天器的运动为 \[{\boldsymbol{\rho}}={\boldsymbol{r_2}}-{\boldsymbol{r_1}}\] \[{\boldsymbol{\ddot \rho}}={\boldsymbol{\ddot r_2}}-{\boldsymbol{\ddot r_1}}={\frac{\mu}{r_1^3}}{\boldsymbol{r_1}}-{\frac{\mu}{r_2^3}}{\boldsymbol{r_2}}+\boldsymbol{f}\] 轨道坐标系在惯性空间以角速度$ \omega$转动，则 \[\boldsymbol{\dot {\rho}}=\boldsymbol{\mathop \rho \limits^ \circ} +{\boldsymbol{\omega}} \times {\boldsymbol{\rho}} \] \[\boldsymbol{\ddot {\rho}}={\mathop \rho \limits^{ \circ \circ }}+{2\omega}\times{\boldsymbol{\mathop \rho \limits^ \circ}} +{\boldsymbol{\omega}}\times \left( { \boldsymbol{\omega}}\times{\boldsymbol{\rho}} \right)+\boldsymbol{\mathop \omega \limits^ \circ}\times {\boldsymbol{\rho}}\] 在轨道坐标系中 \[{\bf{\rho }}{\rm{ = }}x{\bf{i}}{\rm{ + }}y{\bf{j}}{\rm{ + }}z{\bf{k}}\] 代入上式可得 \[{\bf{\ddot \rho }} = \left( {\ddot x - {\omega ^2}x + 2\omega \dot y + \dot \omega y} \right){\bf{i}} + \left( {\ddot y - {\omega ^2}y - 2\omega \dot x - \dot \omega x} \right){\bf{j}} + \ddot z{\bf{k}}\] 又有 \[{ {\bf{r}}_1} = {r_1}{\bf{j}}\] \[{ {\bf{r}}_2} = x{\bf{i}} + \left( { {r_1} + y} \right){\bf{j}} + z{\bf{k}}\] 所以有 \[\frac{\mu }{ {r_1^3}}{ {\bf{r}}_1} - \frac{\mu }{ {r_2^3}}{ {\bf{r}}_2} = \mu r_1^{ - 3}{ {\bf{r}}_1} - \mu {\left[ { {x^2} + { {\left( { {r_1} + y} \right)}^2} + {z^2}} \right]^{ - \frac{3}{2}}}\left( { {\bf{\rho }} + { {\bf{r}}_1}} \right)\] \[ = \mu r_1^{ - 3}{ {\bf{r}}_1} - \mu {\left( {r_1^2 + 2{r_1}y + {\rho ^2}} \right)^{ - \frac{3}{2}}}\left( { {\bf{\rho }} + { {\bf{r}}_1}} \right)\] \[ = \mu r_1^{ - 3}\left[ { { {\bf{r}}_1} - { {\left( {1 + \frac{ {2y}}{ { {r_1}}} + \frac{ { {\rho ^2}}}{ {r_1^2}}} \right)}^{ - \frac{3}{2}}}\left( { {\bf{\rho }} + { {\bf{r}}_1}} \right)} \right]\]

当 $ \rho$相对较小时，$ \rho \ll {r_1}\left( {x \ll {r_1},y \ll {r_1},z \ll {r_1}} \right)$)，忽略 $\rho / {r_1}$的二阶以上项。 而$\alpha