| 基于FFT计算循环相关的内容 | 您所在的位置:网站首页 › 用fft计算自相关函数matlab › 基于FFT计算循环相关的内容 |
基于FFT计算循环相关的内容
|
开场白时域卷积定理卷积时域卷积定理的证明
相关函数自相关函数定义性质自相关系数
互相关函数定义互相关与卷积直观观察图示例子:代码验证
性质互相关系数
线性互相关和循环互相关线性互相关循环互相关
离散傅里叶变换与相关计算CompGCN中循环相关的计算
参考
开场白
最近阅读了CompGCN这篇论文,发现其在计算循环相关的时候使用的并不是时域中的计算,而是先将其变换到频域,时域和频域的一个重要转换就不得不提到傅里叶变换了,如果对傅里叶变换有不了解的地方可以查看我的另一篇文章通俗易懂介绍傅里叶变换,这篇文章主要介绍深一层的知识,和FFT计算循环相关所依据的理论知识。 如果你只想知道循环卷积和循环互相关之间的关系以及怎么在频域中计算循环互相关,那么你只需要看互相关与卷积,离散傅里叶变换与相关计算即可。 时域卷积定理时域卷积定理简单的阐述就是时域卷积,频域相乘。对于卷积,可能有些人又不理解了。 卷积
而为什么说时域进行卷积运算等于频域进行相乘运算呢,是由严格的数学推导的 傅里叶变换的公式不知道大家还记得吗。对该公式有不懂的地方可以查阅我的另一个篇文章。通俗易懂介绍傅里叶变换 F ( w ) = ∫ − ∞ ∞ f ( x ) e − i w x d x F(w)=\int\limits_{-\infty}^{\infty}f(x)e^{-iwx}dx F(w)=−∞∫∞f(x)e−iwxdx 卷积公式为: f ( t ) ∗ g ( t ) = ∫ − ∞ ∞ f ( r ) g ( t − r ) d r f(t)*g(t)=\int_{-\infty}^{\infty} f(r)g(t-r)dr f(t)∗g(t)=∫−∞∞f(r)g(t−r)dr 根据傅里叶变换,对其卷积进行变换得到: φ [ f 1 ( t ) ∗ f 2 ( t ) ] = ∫ − ∞ ∞ f 1 ( t ) ∗ f 2 ( t ) e − j w t \varphi [f_{1}(t)*f_{2}(t)]=\int_{-\infty }^{\infty }f_{1}(t)*f_{2}(t)e^{-jwt} φ[f1(t)∗f2(t)]=∫−∞∞f1(t)∗f2(t)e−jwt = ∫ − ∞ ∞ ∫ − ∞ ∞ f 1 ( r ) f 2 ( t − r ) d r e − j w t d t =\int_{-\infty}^{\infty}\int_{-\infty}^{\infty} f_{1}(r)f_{2}(t-r) dre^{-jwt}dt =∫−∞∞∫−∞∞f1(r)f2(t−r)dre−jwtdt 交换积分顺序 = ∫ − ∞ ∞ ∫ − ∞ ∞ f 2 ( t − r ) e − j w t d t f 1 ( r ) d r =\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f_{2}(t-r)e^{-jwt}dtf_{1}(r)dr =∫−∞∞∫−∞∞f2(t−r)e−jwtdtf1(r)dr 令x = t-r,则t=x+r = ∫ − ∞ ∞ ∫ − ∞ ∞ f 2 ( x ) e − j w ( x + r ) d t − r f 1 ( r ) d r =\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f_{2}(x)e^{-jw(x+r)}dt-rf_{1}(r)dr =∫−∞∞∫−∞∞f2(x)e−jw(x+r)dt−rf1(r)dr = ∫ − ∞ ∞ ∫ − ∞ ∞ f 2 ( x ) e − j w x e − j w r d x f 1 ( r ) d r =\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f_{2}(x)e^{-jwx}e^{-jwr}dxf_{1}(r)dr =∫−∞∞∫−∞∞f2(x)e−jwxe−jwrdxf1(r)dr = ∫ − ∞ ∞ ∫ − ∞ ∞ f 2 ( x ) e − j w x d x f 1 ( r ) e − j w r d r =\int_{-\infty}^{\infty}\int_{-\infty}^{\infty}f_{2}(x)e^{-jwx}dxf_{1}(r)e^{-jwr}dr =∫−∞∞∫−∞∞f2(x)e−jwxdxf1(r)e−jwrdr = F 1 ( f ) F 2 ( f ) =F_{1}(f)F_{2}(f) =F1(f)F2(f) 通过证明我们发现时域的卷积的确为频域的相乘。 同理频域卷积定理与时域卷积定理证明类似,读者可自行推导 φ [ f 1 ( t ) f 2 ( t ) ] = F 1 ( f ) ∗ F 2 ( f ) \varphi [f_{1}(t)f_{2}(t)]=F_{1}(f)*F_{2}(f) φ[f1(t)f2(t)]=F1(f)∗F2(f) 时域相乘等于频域卷积 相关函数概念:相关函数是指描述两个信号X(s),Y(t)在任意两个不同的时刻s、t的取值的相关程度。两个信号之间相似度可以用相关系数来表达。在数模中也是一个常用的公式。 p ( x y ) = C O V ( X , Y ) D ( X ) D ( Y ) p(xy)=\frac{COV(X,Y)}{\sqrt{D(X)}\sqrt{D(Y)} } p(xy)=D(X) D(Y) COV(X,Y) 其中系数越大表示相关程度越高。 相关函数分为自相关和互相关, 自相关表示随机信号在不同时刻t1、t2的取值之间的相关程度 互相关指的是x(t)、y(t)在两个不同时刻t1、t2的取值之间的相关程度 自相关函数 定义自相关函数是对信号自身的负相关,表示一个序列不同时刻的相关程度。它经常用于信号处理的分析函数和序列,例如R(s,t)=E(X(s)*X(t))。类似对自身不同时刻的序列进行卷积。但是又有一些不同。 R ( t , t + r ) = lim T → ∞ 1 T ∫ 0 T x ( t ) x ( t − r ) d t R(t,t+r)=\lim_{T \to \infty } \frac{1}{T}\int\limits_{0}^{T} x(t)x(t-r)dt R(t,t+r)=T→∞limT10∫Tx(t)x(t−r)dt 循环互相关离散形式: ∑ x = − ∞ ∞ f ( x ) f ( x − t ) \sum_{x=-\infty}^{\infty}f(x)f(x-t) x=−∞∑∞f(x)f(x−t) 其中r为一个时域位移信号。与卷积公式对比。 ∫ − ∞ ∞ f ( x ) f ( t − x ) d x \int_{-\infty}^{\infty} f(x)f(t-x)dx ∫−∞∞f(x)f(t−x)dx 离散形式 ∑ x = − ∞ ∞ f ( x ) g ( t − x ) \sum_{x=-\infty}^{\infty}f(x)g(t-x) x=−∞∑∞f(x)g(t−x) 首先是上下限。相关是在他的周期内进行积分,其次就是后半部分的积分函数。自相关为一个函数,相乘,这个函数指的是它自身,卷积是两个函数,二者的形式上比较像。 性质1自相关函数为偶函数,R(t,t+r)=R(t,t-r)。 2当r等于0,自相关函数取得最大值等于信号的均方值 3周期信号的自相关函数仍然为同频率的周期信号 4若随机信号不含有周期的成分,当r趋近于无穷大时,自相关趋近于信号的平方值的平方。 自相关系数p x x ( r ) = R ( t , t + r ) − μ x 2 σ x 2 p_{xx}(r)=\frac{R(t,t+r)-\mu ^{2}_{x}}{\sigma ^{2}_{x}} pxx(r)=σx2R(t,t+r)−μx2 当r等于0,自相关系数为1,说明此时相关程度最大,当r趋近无穷的时候,自相关系数为0,说明x(t)和x(t+r)此时彼此间无关,因此自相关系数可以表示信号间相关的强弱。 互相关函数 定义自相关时互相关的一种特殊情况,互相关是描述两个随机信号x(t)、y(t)的任意两个不同时刻s、t的取值之间的相关程度,定义为 R ( s , t ) = E ( X ( s ) ∗ Y ( t ) ) R(s,t)=E(X(s)*Y(t)) R(s,t)=E(X(s)∗Y(t)) 对于连续函数 R ( s , t ) = lim T → ∞ 1 T ∫ − ∞ ∞ x ( t ) g ( t − r ) d t R(s,t)=\lim_{T \to \infty } \frac{1}{T}\int\limits_{-\infty}^{\infty} x(t)g(t-r)dt R(s,t)=T→∞limT1−∞∫∞x(t)g(t−r)dt 正确的表达式g函数应该是是g(t+r),相当于左移,但是t-r相当于右移,但是你同时把g函数和x函数的序列更换,她的计算结果是一样的。因为两个序列对应相乘的位置没有发生变化,因此我这里写成t-r,为了方便与卷积进行对比。 互相关与卷积 直观观察将上述公式与卷积对比 ∫ − ∞ ∞ f ( x ) g ( t − x ) d x \int_{-\infty}^{\infty} f(x)g(t-x)dx ∫−∞∞f(x)g(t−x)dx 我们将循环相关的一个序列进行反转。 ∫ − ∞ ∞ x ( t ) g ( r − t ) d t \int\limits_{-\infty}^{\infty} x(t)g(r-t)dt −∞∫∞x(t)g(r−t)dt 是不是可以发现循环相关中的t为卷积中的x,r相当于卷积中t。 二者都是滑动序列相乘互相关的两个序列都不进行翻转,卷积其中一个序列需要先翻转在进行滑动相乘求和,所以两个序列做相关就是将一个序列翻转之后做卷积,这句话大家细品。CompGCN正是应用了这个原理进行循环相关的运算。 图示例子:
这里x序列为[1,2,3],y序列为[4,5,6]。 当r等于0的时候,代入到循环互相关的公式中,我们对应相乘为(1–4)、(2–5)、(3–6)。而在卷积中,我们的对应相乘为(1–6)、(2–5)、(3–4)我们可以显而易见的发现,卷积运算进行翻转对应的就是循环互相关。 代码验证相关计算和卷积关系代码验证: x = [2,0,0,1]; h = [1,0,-1,2]; y1 = xcorr(x,h) y2 = conv(x,flip(h)) % y1 = [2,0,-2,4,1,0,-1,2] % y2 = [2,0,-2,4,1,0,-1,2] 二者的结果是一样的互相关函数反应的是两个函数在不同的位置上的对应程度。 性质1、互相关函数不是偶函数,是不对称的。相当于进行平移,下路为x(t)f(t)序列和其互相关序列 p x y ( r ) = R ( x ( t ) , y ( t + r ) ) − μ x μ y σ x σ y p_{xy}(r)=\frac{R(x(t),y(t+r))-\mu_{x}\mu_{y}}{\sigma_{x}\sigma_{y}} pxy(r)=σxσyR(x(t),y(t+r))−μxμy 互相关系数越大则表示其含有较多的同频率的周期成分,当r很大时,彼此无关,那么互相关系数就为0. 线性互相关和循环互相关正如卷积分为循环卷积和线性卷积,互相关也有线性相关和循环互相关。 线性互相关
通过观察相关和卷积的公式,在互相关的时候我让大家细品了一句话,大家还记得吗,现在来回顾一下这句话,卷积和互相关的区别就在于翻转,一个序列进行翻转后在进行卷积那么就是互相关,哎嘿好神奇,而我们在开头又进行了时域卷积和频域相乘的证明,通过转换到频域可以降低其计算的复杂度,数据越大效果越好,所以在CompGCN中使用了频域来计算他的一个循环相关,诶嘿,线索传到一起了,也达到了我掌握代码中求循环相关的原理,果真皇天不负有心人。下面来总结一下计算流程,在一步一步的进行分析。 对两个序列进行DFT,快速算法采用FFT进行傅立叶变换对一个序列进行翻转(频域共轭)翻转后做卷积(频域相乘)进行逆傅里叶变换得到结果。
通过上述的分析,我们大抵知道了使用频域计算循环相关的流程。CompGcn我们用FFT来替换DFT降低在大型图网络中计算的时间复杂度。 通过观察CompGCN当中的源码,在CompGCN_Conv.py中寻找到计算循环相关的函数。 这里作者用了torch.rfft(a,1)表示作者对向量进行进行快速傅里叶变换。 作者在对a向量进行傅里叶变换之后使用conj这个函数,我们在help.py文件下找到该函数。 代码验证 import torch import torch.nn.functional as F def circular_correlation(A, B): # 计算傅里叶变换 fft_A = torch.fft.fft2(A, dim=(-2, -1)) fft_B = torch.fft.fft2(B, dim=(-2, -1)) # 取复共轭并进行元素乘积 conj_fft_B = torch.conj(fft_B) fft_prod = fft_A * conj_fft_B # 计算逆傅里叶变换并取实部 correlation = torch.fft.ifft2(fft_prod, dim=(-2, -1)).real return correlation if __name__ == "__main__": # 假设A和B是输入的两个信号,具有相同的形状 A = torch.tensor([[1.0, 2.0, 3.0]]) B = torch.tensor([[0.0, 1.0, 0.0]]) # 调用函数计算循环互相关 result = circular_correlation(A, B) print(result) #result=>tensor([[2., 3., 1.]])
自相关与互相关 离散傅里叶变换与相关性计算 python中…的含义 |
【本文地址】
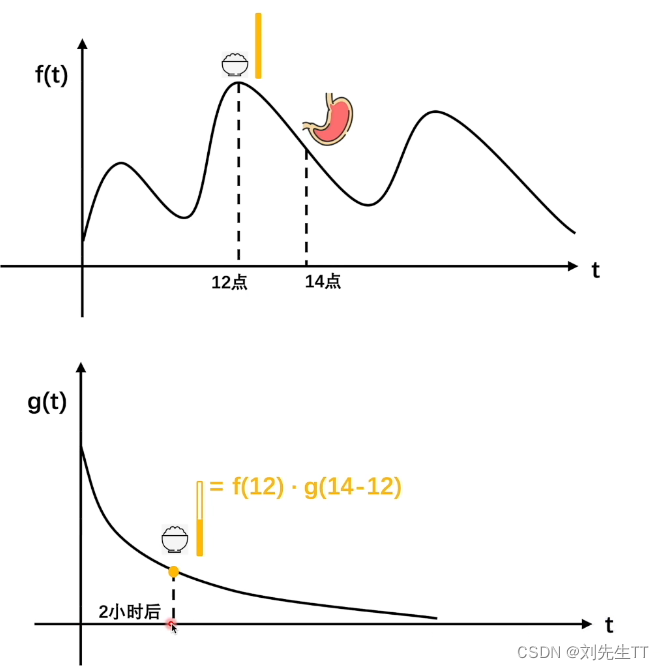 假设你正在吃食物,其中f(t)记录了你在不同时间点吃的食物的量,g(t)计算了你的消化速率,表示你肚子中随着时间的流逝还剩的某种食物的占比,假设你在12点吃了米饭,那么我要求你计算14点你肚子里面剩余的米饭。你会怎么计算,别急,先思考一下。 | | | | | | | | | | 没错,就是用f(12)*g(14-12),f(12)代表你进食的米饭的量,而g(14-12)代表你过了两个小时之后肚子里剩余的米饭的占比,总量乘上剩余的占比=剩余的量,没错。那么如果我在8点、10点、12点、14点均吃了东西,我应该怎么计算呢?
假设你正在吃食物,其中f(t)记录了你在不同时间点吃的食物的量,g(t)计算了你的消化速率,表示你肚子中随着时间的流逝还剩的某种食物的占比,假设你在12点吃了米饭,那么我要求你计算14点你肚子里面剩余的米饭。你会怎么计算,别急,先思考一下。 | | | | | | | | | | 没错,就是用f(12)*g(14-12),f(12)代表你进食的米饭的量,而g(14-12)代表你过了两个小时之后肚子里剩余的米饭的占比,总量乘上剩余的占比=剩余的量,没错。那么如果我在8点、10点、12点、14点均吃了东西,我应该怎么计算呢?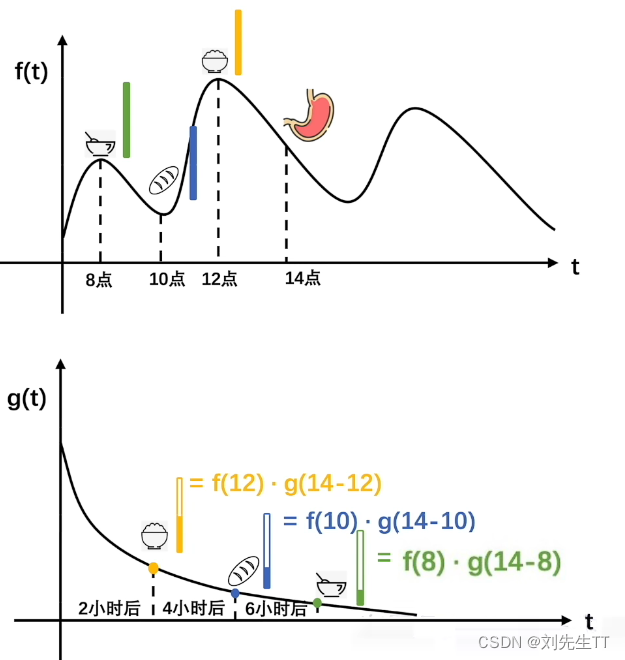 没错,就是将各个时间段到14点剩余的量加到一起就好了。 剩余的量=f(12)*g(14-12)+f(10)*g(14-10)+f(8)*g(14-8) 你已经理解了卷积的意义了,你没听过,上述的计算过程就是卷积
∫
−
∞
∞
f
(
x
)
g
(
t
−
x
)
d
x
\int_{-\infty}^{\infty} f(x)g(t-x)dx
∫−∞∞f(x)g(t−x)dx 上述公式就是卷积公式,用之前的例子讲解,就是将各个时间吃的食物,到当前时刻剩余的量的一个总和。
没错,就是将各个时间段到14点剩余的量加到一起就好了。 剩余的量=f(12)*g(14-12)+f(10)*g(14-10)+f(8)*g(14-8) 你已经理解了卷积的意义了,你没听过,上述的计算过程就是卷积
∫
−
∞
∞
f
(
x
)
g
(
t
−
x
)
d
x
\int_{-\infty}^{\infty} f(x)g(t-x)dx
∫−∞∞f(x)g(t−x)dx 上述公式就是卷积公式,用之前的例子讲解,就是将各个时间吃的食物,到当前时刻剩余的量的一个总和。
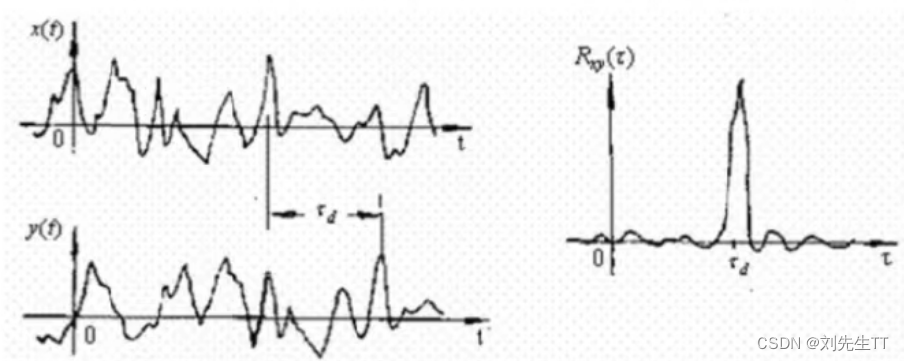 2、x(t)与 (t)互换后,它们的互相关函数对称于纵轴,说明使信号 y(t)在时间上导前与使另一信号 x(t)滞后,其结果是一样的。Rxy(t) =R(x(t),y(t-r))
2、x(t)与 (t)互换后,它们的互相关函数对称于纵轴,说明使信号 y(t)在时间上导前与使另一信号 x(t)滞后,其结果是一样的。Rxy(t) =R(x(t),y(t-r)) 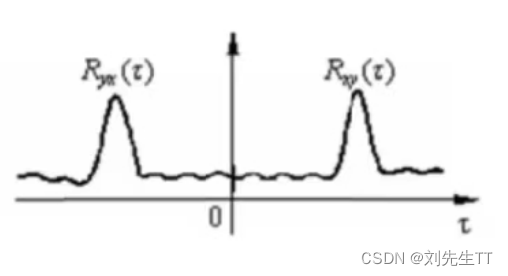 3、若两个随机信号 x(t)和 y(t)没有同频率周期成分,是两个完全独立的信号,则当t趋近于无穷多个时候,
lim
t
→
∞
R
x
y
(
t
)
=
μ
x
μ
y
\lim_{t \to \infty} R_{xy}(t)=\mu _{x}\mu_{y}
t→∞limRxy(t)=μxμy
3、若两个随机信号 x(t)和 y(t)没有同频率周期成分,是两个完全独立的信号,则当t趋近于无穷多个时候,
lim
t
→
∞
R
x
y
(
t
)
=
μ
x
μ
y
\lim_{t \to \infty} R_{xy}(t)=\mu _{x}\mu_{y}
t→∞limRxy(t)=μxμy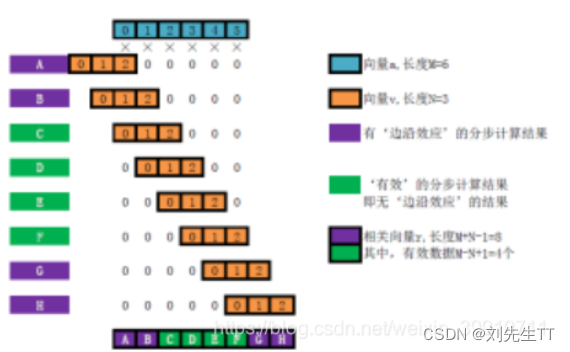 线性互相关类似滑动卷积,其最后计算出的长度为N+M-1,线性相关的实际意义通过其计算公式可以观察出来,为向量a中的各个向量与向量v等长的子向量与向量v的子向量的相似程度,说白了就是,向量v与向量a的子向量一个一个比,看看与每个子向量的相似的程度,
线性互相关类似滑动卷积,其最后计算出的长度为N+M-1,线性相关的实际意义通过其计算公式可以观察出来,为向量a中的各个向量与向量v等长的子向量与向量v的子向量的相似程度,说白了就是,向量v与向量a的子向量一个一个比,看看与每个子向量的相似的程度,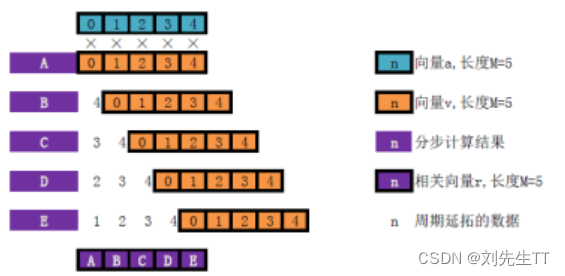 循环互相关的计算公式如上,类似于卷积,不过不是将多出的部分补0,而时进行周期延拓。循环互相关表征的时两个等长的周期性数据在不同的时刻的相似程度。
循环互相关的计算公式如上,类似于卷积,不过不是将多出的部分补0,而时进行周期延拓。循环互相关表征的时两个等长的周期性数据在不同的时刻的相似程度。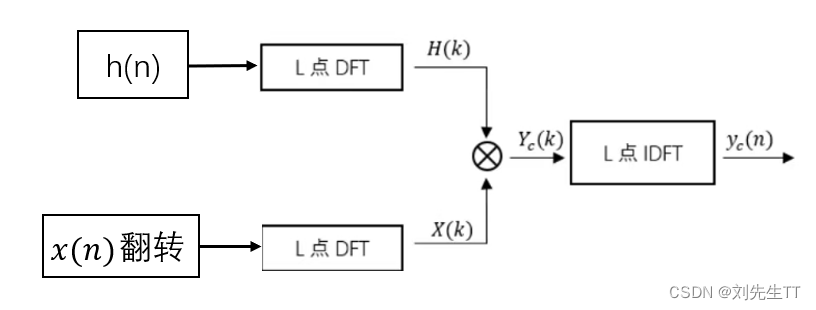 通过信号系统这门课的学习,我们知道时域翻转 频域取共轭,很简单的证明,傅里叶变换是将时域变换成频域,而在傅里叶变换中我们讲了,频域是由各个正弦波和余弦波组成,我们在频域通过复平面来进行表示,其中实部是偶函数(cos),虚部是奇函数(sin),对其取反,相当于cos不变,sin取反,实部不变,虚部取反,等于共轭。有的人又有疑问了,为什么取负就是翻转了呢?因为y序列我们在对其进行循环卷积的时候对其进行周期拓展,你将取负后平移到原来的位置,你会发现,最后一个变成第一个的神奇,而在卷积运算中最重要的一步就是平移,慢慢平移到原来的位置,达到和翻转一样的效果,因此取负就是翻转。
通过信号系统这门课的学习,我们知道时域翻转 频域取共轭,很简单的证明,傅里叶变换是将时域变换成频域,而在傅里叶变换中我们讲了,频域是由各个正弦波和余弦波组成,我们在频域通过复平面来进行表示,其中实部是偶函数(cos),虚部是奇函数(sin),对其取反,相当于cos不变,sin取反,实部不变,虚部取反,等于共轭。有的人又有疑问了,为什么取负就是翻转了呢?因为y序列我们在对其进行循环卷积的时候对其进行周期拓展,你将取负后平移到原来的位置,你会发现,最后一个变成第一个的神奇,而在卷积运算中最重要的一步就是平移,慢慢平移到原来的位置,达到和翻转一样的效果,因此取负就是翻转。 在help.py中找到该函数
在help.py中找到该函数 
 a[…:,1]表示对傅里叶变换后所有的虚部取反,也就是取共轭。相当于在时域进行了翻转。在进行翻转后又对两序列使用com_mult函数,该函数表示两个复数相乘,在这里也就是对频域进行相乘, 在两个向量中的一个取共轭之后,此时就可以用卷积来计算相关了,但是由于时域计算卷积复杂度高,因此我们用时域卷积定理,将时域卷积变换成频域的相乘。相乘函数为
a[…:,1]表示对傅里叶变换后所有的虚部取反,也就是取共轭。相当于在时域进行了翻转。在进行翻转后又对两序列使用com_mult函数,该函数表示两个复数相乘,在这里也就是对频域进行相乘, 在两个向量中的一个取共轭之后,此时就可以用卷积来计算相关了,但是由于时域计算卷积复杂度高,因此我们用时域卷积定理,将时域卷积变换成频域的相乘。相乘函数为  r1,i1代表第一个向量的实部和虚部,r2,i2代表第二个向量的实部虚部。 复数相乘为
(
a
+
b
i
)
(
c
+
d
i
)
=
(
a
c
−
b
d
)
+
(
b
c
+
a
d
)
i
(a+bi) (c+di)= (ac-bd)+ (bc+ad)i
(a+bi)(c+di)=(ac−bd)+(bc+ad)i a,b,c,d分别替换为r1,i1,r2,i2进行计算。 将计算后的结果通过torch.stack()函数进行拼接。最后通过torch.rfft对其进行逆变换返回到时域。
r1,i1代表第一个向量的实部和虚部,r2,i2代表第二个向量的实部虚部。 复数相乘为
(
a
+
b
i
)
(
c
+
d
i
)
=
(
a
c
−
b
d
)
+
(
b
c
+
a
d
)
i
(a+bi) (c+di)= (ac-bd)+ (bc+ad)i
(a+bi)(c+di)=(ac−bd)+(bc+ad)i a,b,c,d分别替换为r1,i1,r2,i2进行计算。 将计算后的结果通过torch.stack()函数进行拼接。最后通过torch.rfft对其进行逆变换返回到时域。 这里我使用的是torch.fft.fft2函数,读者可以自行选择快速傅里叶变换,来进行结果的验证。 至于为什么使用快速傅里叶变换可以降低运算的复杂度,我找到了一篇比我解释的好百倍的通俗易懂的文章。其原理就是采用分而治之的思想,将DFT的复杂度O(n*n)降低到O(nlogn)快速傅里叶变换
这里我使用的是torch.fft.fft2函数,读者可以自行选择快速傅里叶变换,来进行结果的验证。 至于为什么使用快速傅里叶变换可以降低运算的复杂度,我找到了一篇比我解释的好百倍的通俗易懂的文章。其原理就是采用分而治之的思想,将DFT的复杂度O(n*n)降低到O(nlogn)快速傅里叶变换