| 交错级数如何判断收敛 | 您所在的位置:网站首页 › 狄利克雷审敛法证明 › 交错级数如何判断收敛 |
交错级数如何判断收敛

追不上的上古玄武告诉我们:无穷个正数加在一起不一定是正无穷。以此为开端,有了极限的观念,还有了级数的观念。很多数列的Sn很难求,这篇文章只讨论极其片面的判断常数项级数是否收敛的十一个方法。 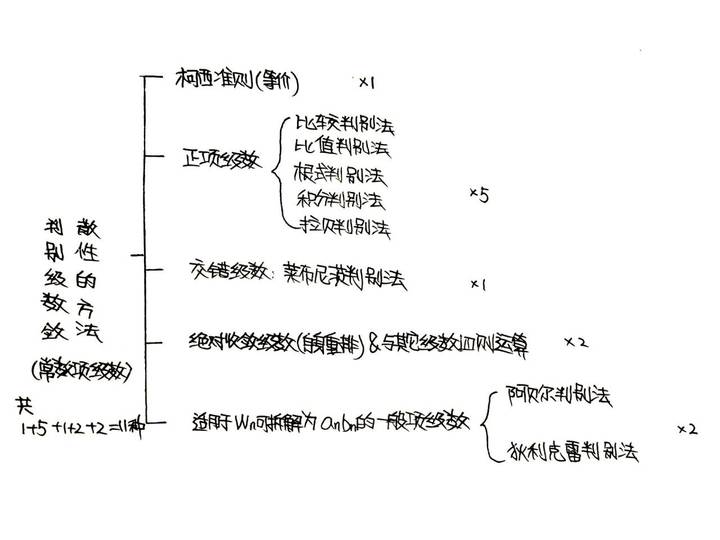 PART 1 对于十一种(级数敛散性)判别法的粗糙总结
PART 1 对于十一种(级数敛散性)判别法的粗糙总结
→(我会在part1的结尾写出我对于这11种判别法使用顺序或是优先选择哪个方法的流程图,如果您对哪个方法印象不深可以跳着看,如果您对这11种方法了如指掌的话直接跳转到part1末尾的图即可啦。) (1)级数收敛的柯西准则及其两个衍生品(⭐⭐⭐⭐⭐): 我觉得直观的对级数∑u(n)收敛的定义应该是这样的:lim(n->∞)Sn=A ; 这个直观的定义和级数收敛的柯西准则是等价的,但这个直观的定义直接拿来作为判别法的应用价值实在低得很,原因是这样的:∀ε>0,∃正整数N,当n>N时,A-ε0的。 这五种方法是有家庭关系的,如图:(这是这篇文章很重要的两张图里的第一张 ) 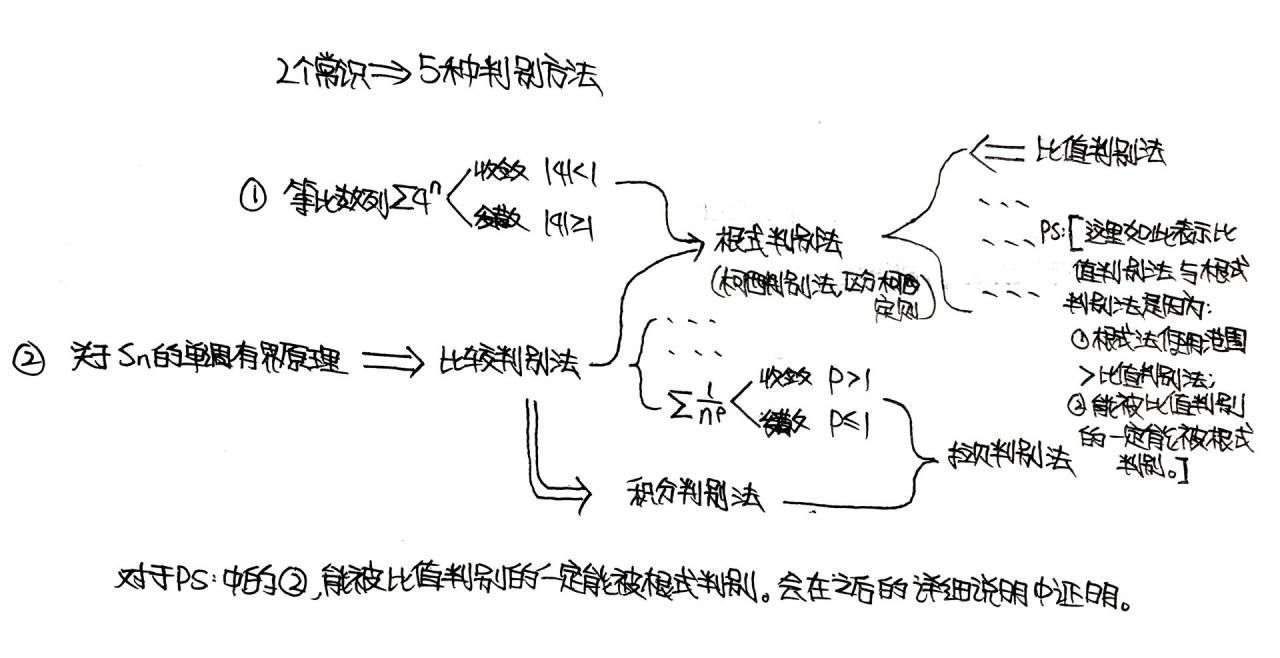
Segment 1:比较判别法&积分判别法 这两个方法只是依靠了单调有界定理,并没有借助任何任何已知的收敛或发散数列。 
比较判别法是对两个级数进行操作的,而且至少有一个级数敛散性要已知,通常遇到判断单独一个级数敛散性的时候我们要通过放缩来与记忆中已知敛散性的级数进行比较,如果运气好是可以比出大小判断敛散性的。 
Segment 2:比值判别法(达朗贝尔判别法)&根式判别法(柯西判别法) 如上面的家庭关系图所示:在引入了等比(数列)级数(公比的取值范围确定敛散性)之后,就有了比值判别法和根式判别法。 
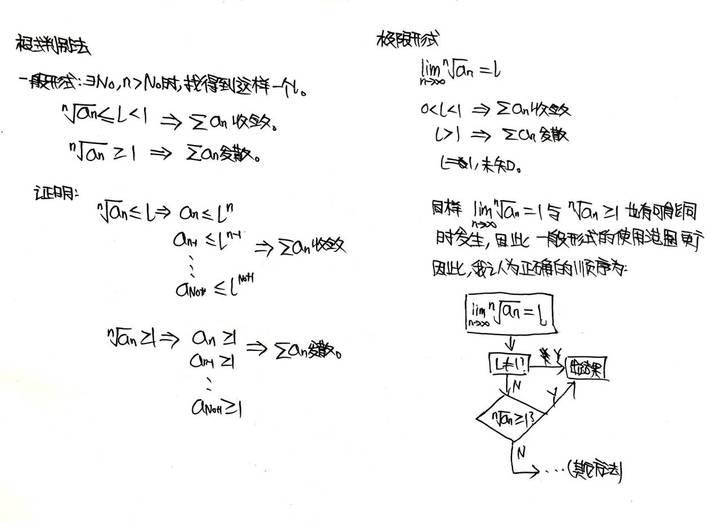
下面这两张图是关于“一切可以用(极限形式下)比值判别法判断敛散性的级数也一定可以用(极限形式下)根式判别法判断敛散性&根式判别法适用范围大于比值判别法”的证明。 
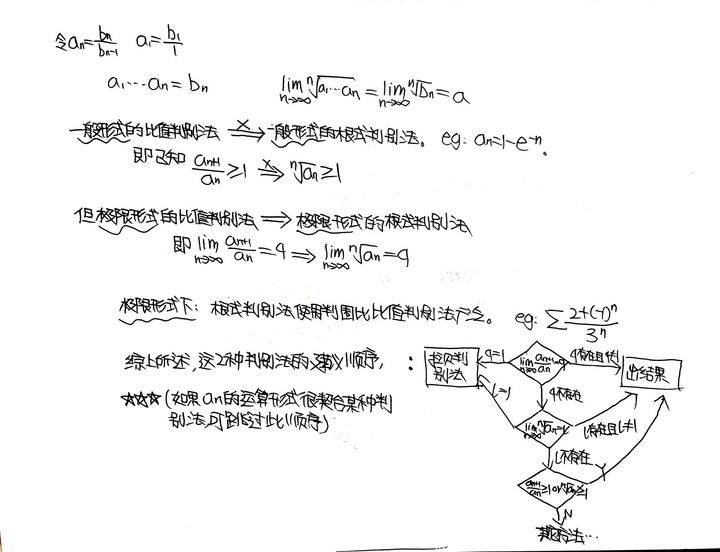
Segment 3:拉贝判别法 比值判别法和根式判别法是与等比级数进行比较得到的结果,拉贝判别法是与调和级数比较得到的结果。 
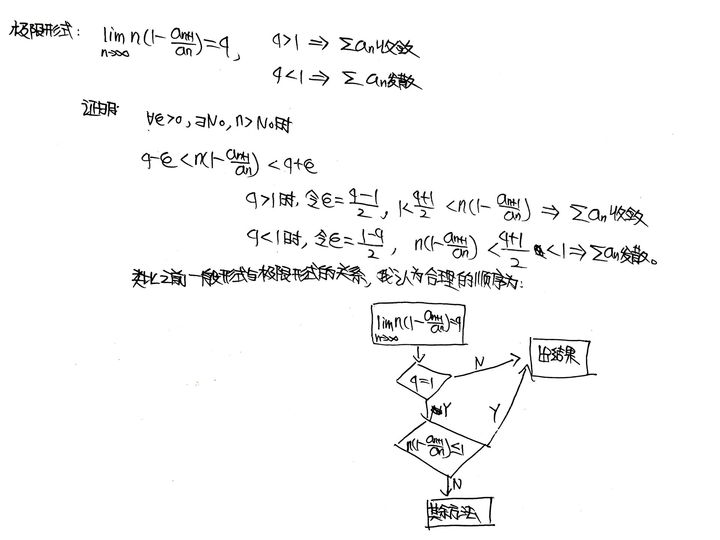
(3)交错级数的莱布尼茨判别法(⭐⭐⭐) 交错级数敛散性的判别法一定是这十一个方法里辨识度最高的也是用法最简单的了。这里只需要强调一点:交错级数收敛≠>数列绝对值单调减。反例:an=(-1)^n / 2^[n+(-1)^n]。这个数列的绝对值小于1/2^(n-1),因此该级数收敛,但是|a2|=1/8,|a3|=1/2。推而广|a(2n+1)|>|a(2n)| 
( 4)绝对收敛级数(自身重排)&与其他级数四则运算(⭐⭐⭐⭐) 这一块还是很有趣的,不像前面的方法那样死板枯燥。 Segment 1 级数自身的重排 最开始需要2个重要的结论: (1) 正项(负项)收敛级数的重排仍是正项(负项)收敛级数,且重排前与重排后的两个级数收敛于同一个值。 (2) 正项(负项)发散级数的重排仍是正项(负项)发散级数,且重排前与重排后的两个级数都发散于正无穷(负无穷)。 证明: 

还差最后一个没有讨论,一般项的发散级数重排可能收敛也可能发散。本身就发散,所以调换有限项以后得到的级数依然发散。上面还证明了一般项条件收敛级数的重排列可能发散,由于重排是可逆的,所以一般项发散级数的重排可能收敛。 总结: 
Segment 2 级数加括号 加括号是很好理解的,就是数列Sn(Sn=∑an)与Sn子数列(Sn子数列=∑a i(n) )的关系。原数列发散则子列收敛,子列收敛,原数列不一定收敛,但是一个数列的所有子列收敛于同一个值那么原数列收敛。(其实和加括号具有增加收敛性的意思差不多) 综上所述:级数收敛,加括号后一定收敛。逆否之,级数发散,去括号后一定发散。 级数收敛,去括号(裂项)后不一定收敛。 (比如0+0+……=(1-1)+(1-1)+……≠1-1+1-1+……)。 Segment 3 级数的乘法&加法运算 这一部分我打算由浅入深的写(其实都很浅显),但我会尽最大努力做到严谨的。一定成立的结论写证明,不一定成立的结论写反例。 

上面六种粗分情况中,有四种是不一定,既然有绝对收敛与条件收敛这个细分,那么对于d等式左侧带有收敛的算式(情况1,2)加入这两个细分的限定条件以后,不一定里会不会出现一定呢。同时第一种情况也可以从绝对收敛条件收敛的角度重新考虑。 
综上所述:把一定成立的结论列举出来权当总结: (一):加法 (1)绝对收敛+绝对收敛=绝对收敛 (2)条件收敛+绝对收敛=条件收敛 (3) 条件(绝对)收敛+发散=发散 (二):乘法 绝对收敛×有界数列(绝对,条件收敛数列都是有界数列)=绝对收敛(⭐⭐⭐⭐⭐) (这句话的应用范围非常广阔,阿贝尔定理(注意是阿贝尔定理,区分它和阿贝尔引理)就是这句话推出来的。) (5)适用于一般项级数的阿贝尔判别法和狄利克雷判别法(⭐) 这两种判别方法其实是另一种分类方式(单调数列,有界数列)的乘法运算中的两个一定成立的特例。 
之后结合阿贝尔引理和柯西准则,只要再对an,bn添加一些附加条件使得在"N项之后"【max{aN+1,aN+2...an}是一个类似无穷小的值】or【大于N后,A这个界是个类无穷小值】就可以了。 如果an单调有界,那么max那块就是个确定的数,同时∑bn收敛,那么大于N时,即 b(N+1)+b(N+2)+......的绝对值小于一个类无穷小量。这就是阿贝尔判别法,an单调有界,∑bn收敛,那么∑anbn 收敛。 如果an单调有界,那么an收敛,假设an收敛于0的话,max项变成了一个类无穷小项。此时只要∑bn 有界就可以了。这就是狄利克雷判别法,an单调有界,收敛于0。∑bn有界,那么∑anbn 收敛。 PART 1 总结图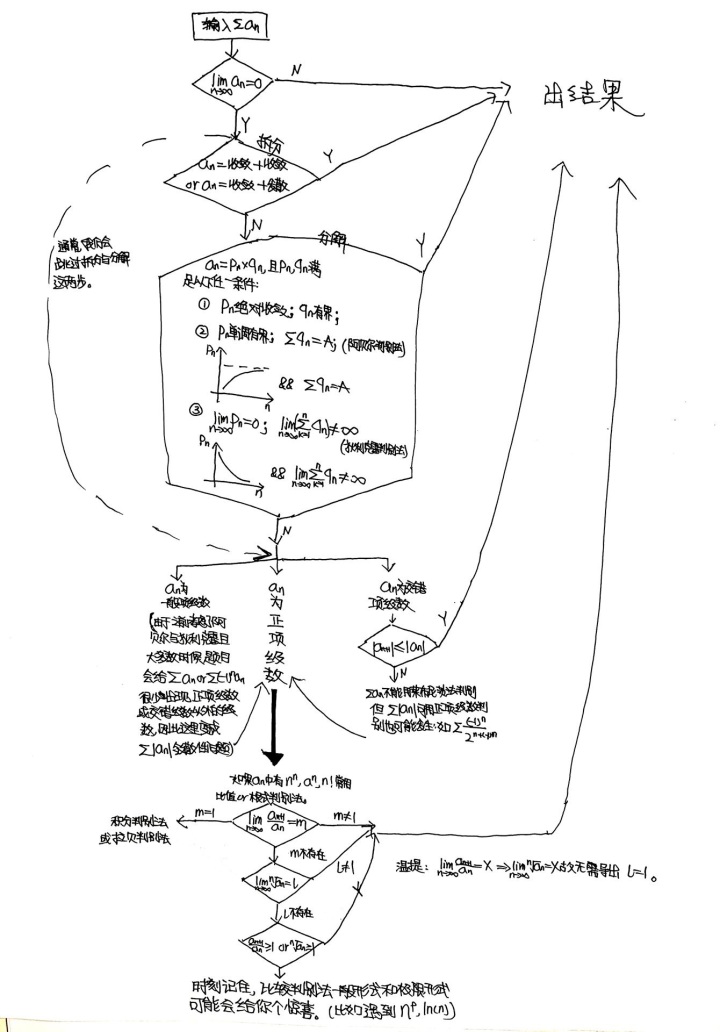
PS:黔驴技穷时(当比较判别法的一般形式和极限形式都无法带给你奇迹)再去用拉贝审敛法或者最原始的柯西准则。 PART 2 11道好玩的题提前说明: 这11道题并不难而且很常见,我只是单纯的觉得这是11道题好玩罢。 


终于写完啦✌! |
【本文地址】