稳态热传导

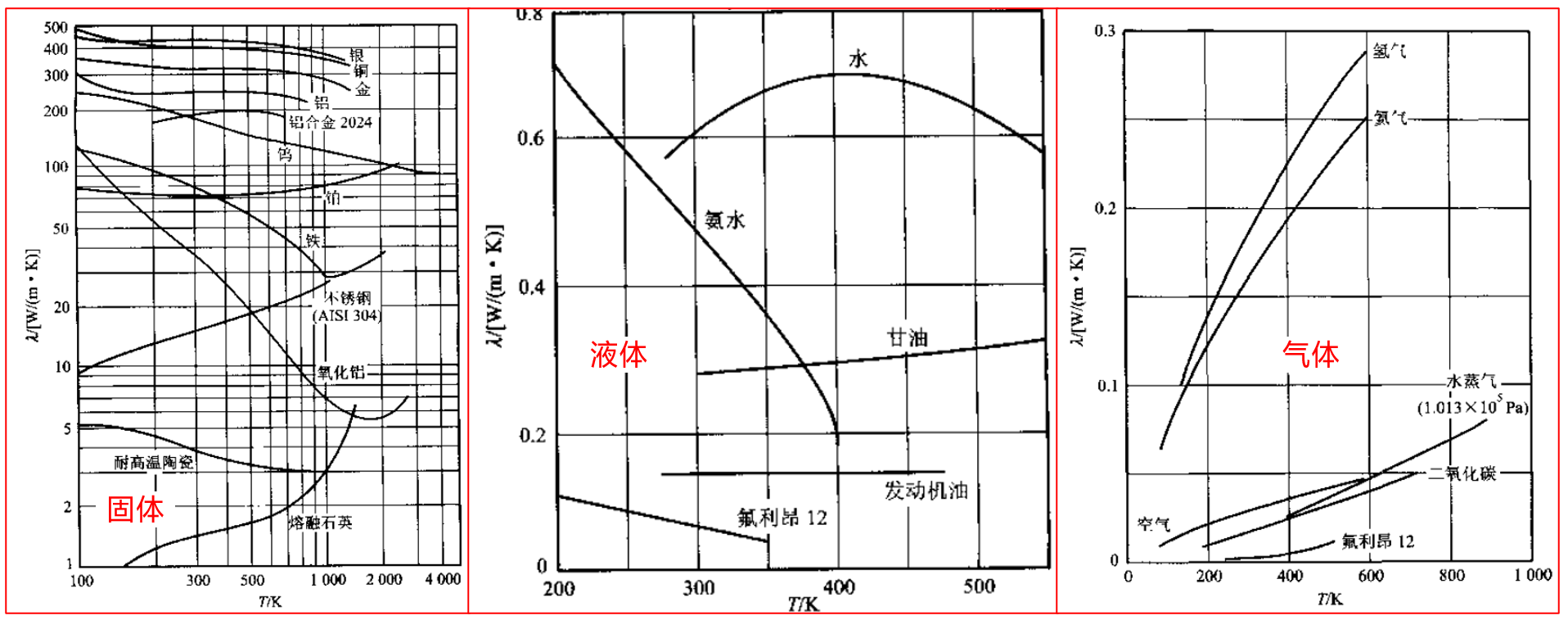
本文参考杨世铭、陶文铨所著《传热学》第四版第二章。不同状态下物质导热机理各不相同，但宏观上都可以通过傅里叶定律来描述其内部温度变化。气体中，导热是气体分子不规则热运动相互碰撞的结果，气体温度越高，分子运动动能越大。不同能量水平的分子相互碰撞的结果，使热量从高温处传递到低温处。对于固体，导电固体中有相当多的自由电子，它们在晶格之间像气体分子那样运动（称为电子气），自由电子的运动在导电固体的导热中起着主要作用。在非导电固体中，导热是通过晶格结构的振动，即原子、分子在其平衡位置附近的振动来实现的。晶格结构振动的传递在文献中常称为弹性声波，其量子化表示为声子，与辐射能量的量子化表示——光子相类似。至于液体中导热机理，存在不同观点。一种观点认为定性上类似于气体，只是情况更复杂，因为液体分子间的间距比较近，分子间的作用力对碰撞过程的影响远比气体大。另一种观点则认为液体的导热机理类似于非导电固体，主要靠弹性声波的作用。

一般来说，物体的温度场是坐标与时间的函数，即 \[ T = f(x,y,z,t). \] 稳态温度场（steady temperature filed）中各点温度不随时间变化，随时间变化称为非稳态温度场或瞬态温度场（unsteady or transient temperature field）。

三维空间内，热流密度是一个矢量，记为\(~\boldsymbol{q}\)。描述导热的傅里叶定律写为 \[ \boldsymbol{q} = -\lambda \nabla T, \] 其中\(~\nabla T~\)是空间某点的温度梯度（temperature gradient），笛卡尔坐标系（Cartesian coordinates）下该值为 \[ \nabla T = \frac{\partial T}{\partial x}\boldsymbol{e}_x + \frac{\partial T}{\partial y}\boldsymbol{e}_y + \frac{\partial T}{\partial z}\boldsymbol{e}_z, \] 其中\(~\boldsymbol{e}_x\)、\(\boldsymbol{e}_y\)、\(\boldsymbol{e}_z~\)分别是\(~x\)、\(y\)、\(z~\)方向的单位矢量。

测量导热系数的方法有稳态法和非稳态法两大类，傅里叶定律是稳态测定的基础。导热系数数值取决于物质的种类和温度，金属的导热系数很高。常温（20℃）下金属导热系数的典型值是：纯铜为 399 W/(m·K)、碳钢（含碳量 1.5%）为 36.7W/(m·K)。气体的导热系数很小，如时干空 20℃ 气的导热系数为 0.0259 W/(m·K)。液体数值介于金属和气体之间， 20℃ 时水的导热系数为 0.599 W/(m·K)。习惯上把导热系数小的材料称为保温材料，又称隔热材料或绝缘材料（insulating material）。1992 年我国国家标准定义平均温度不高于 350℃ 时导热系数不大于 0.12 W/(m·K) 的材料称为保温材料。下图为常见材料导热系数随温度的变化

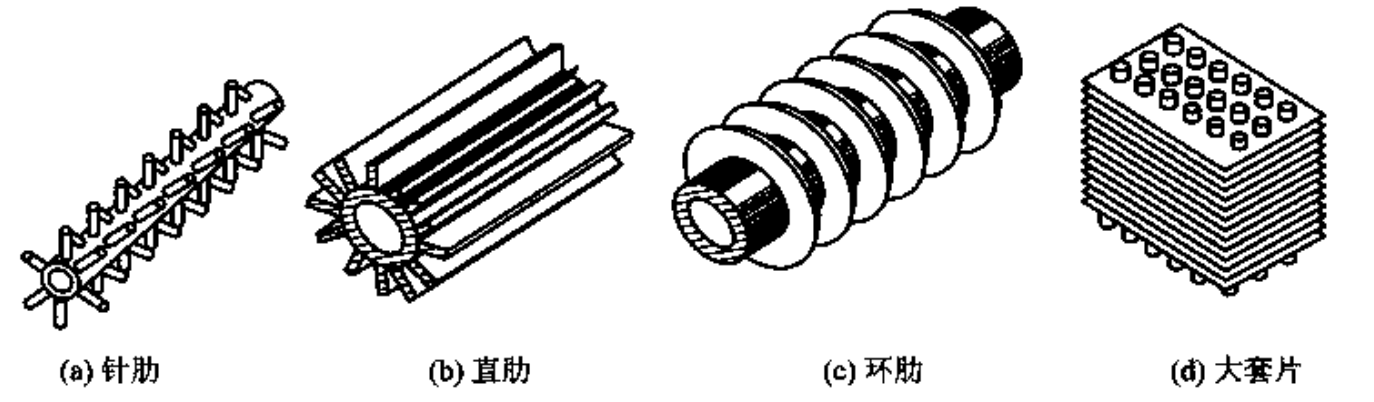
笛卡尔坐标系下三维非稳态导热微分方程一般形式写作 \[ \begin{align}\label{ht_conduction} \rho C_p \frac{\partial T}{\partial t} = \frac{\partial}{\partial x}\left(\lambda \frac{\partial T}{\partial x}\right) + \frac{\partial}{\partial y}\left(\lambda \frac{\partial T}{\partial y}\right) + \frac{\partial}{\partial z}\left(\lambda \frac{\partial T}{\partial z}\right) + \dot{\Phi}, \end{align} \] 其中\(~\rho\)、\(C_p~\)和\(~\dot{\Phi}~\)分别为密度、比热容和体积热源，其单位分别为 kg/m3，J/(Kg·K) 和 W/m3。

式\(~\eqref{ht_conduction}~\)化简为 \[ \begin{align}\label{ht_conduction2} \frac{\partial T}{\partial t} = a\left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} \right) + \frac{\dot{\Phi}}{\rho C_p}, \end{align} \] 其中\(~a=\lambda/(\rho C_p)~\)称为热扩散率或热扩散系数（thermal diffusivity），单位为 m2/s。

式\(~\eqref{ht_conduction}~\)化简为 \[ \frac{\partial T}{\partial t} = a\left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} \right), \] 这就是常物性、无内热源的三维非稳态导热微分方程。

式\(~\eqref{ht_conduction}~\)化简为 \[ \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} + \frac{\dot{\Phi}}{\lambda} = 0, \] 数学上，上式称为泊松（Poisson）方程。

式\(~\eqref{ht_conduction}~\)化简为以下拉普拉斯（Laplace）方程 \[ \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} = 0. \]

非稳态导热，在边界上，有 \[ T_\text{w} = f_1(t). \]

非稳态导热，在边界上，有 \[ -\lambda\left( \frac{\partial T}{\partial n} \right)_\text{w} = f_2(t), \] 其中，\(n~\)为表面的法线方向。

以物体被冷却为例，有 \[ -\lambda \left( \frac{\partial T}{\partial n} \right)_\text{w} = h(T_\text{w}-T_\text{f}). \] 以上三种边界条件与数学物理方程理论中的三类边界条件相对应，又分别称为 Dirichlet 条件、Neumann 条件和 Robin 条件。在处理复杂的实际工程问题时，还会遇到以下情形

\[ -\lambda \frac{\partial T}{\partial n} = \varepsilon\sigma(T_\text{w}^4-T_\text{e}^4). \]

\[ T_1 = T_2,\quad \left( \lambda \frac{\partial T}{\partial n} \right)_1 = \left( \lambda \frac{\partial T}{\partial n} \right)_2. \]

由式\(~\eqref{ht_conduction2}~\)中热扩散率的定义\(~a=\lambda/(\rho C_p)~\)可知

从另一个角度看，\(a~\)越大，材料中温度变化传播得越迅速，可见\(~a~\)也是材料传播温度变化能力大小的指标，并因此有导温系数之称。

傅里叶定律实际上是基于热扰动的传递速度无限大的假定之上的， 对于下列三种情形，傅里叶定律及导热微分方程是不适用的：

厚度为\(~\delta~\)、两个壁面分别维持恒定温度\(~T_1~\)和\(~T_2~\)的平壁，导热数学描述为 \[ \begin{align} \frac{\mathrm{d}^2 T}{\partial x^2} = 0. \end{align} \] 边界条件为 \[ \begin{aligned} x = 0, T = T_1; \\ x = \delta, T = T_2. \end{aligned} \] 则该平壁的温度分布为 \[ T = \frac{T_2-T_1}{\delta} x + T_1. \] 热流密度为 \[ q = \frac{\lambda}{\delta}(T_2-T_1). \] 热流量为 \[ \Phi = A \frac{\lambda}{\delta}(T_2-T_1). \]

\(n~\)层多层壁的计算公式是 \[ q = \frac{T_1 - T_2}{\sum_{i=1}^n \frac{\delta_i}{\lambda_i}}. \]

考察内外半径分别为\(~r_1\)、\(r_2~\)的圆筒壁，其内、外表面温度分别维持均匀恒定的温度\(~T_1~\)和\(~T_2\)。采用柱坐标系\(~(r,\theta,z)~\)描述圆筒导热，则其数学描述和边界条件分别为 \[ \begin{align} \frac{\mathrm{d}}{\mathrm{d}r}\left(r\frac{\mathrm{d}T}{\mathrm{d}r}\right) = 0 \end{align} \] 和 \[ \begin{aligned} r = r_1, T = T_1; \\ r = r_2, T = T_2. \end{aligned} \] 则温度分布为 \[ T = T_1 + \frac{T_2-T_1}{\ln(r_2/r_1)}\ln(r/r_1). \] 热流密度为 \[ q = -\lambda\frac{\mathrm{d}T}{\mathrm{d}r} = \frac{\lambda}{r}\frac{T_1-T_2}{\ln(r_2/r_1)}. \] 热流量为 \[ \Phi = 2\pi rlq = \frac{2\pi\lambda l(T_1-T_2)}{\ln(r_2/r_1)}, \] 其中\(~l~\)是圆筒长度。

导热热阻为 \[ R = \frac{T_2-T_1}{\Phi} = \frac{\ln(r_2/r_1)}{2\pi\lambda l}. \]

温度分布 \[ T = T_2 + (T_1-T_2)\frac{1/r-1/r_2}{1/r_1-1/r_2}. \] 热流量 \[ \Phi = \frac{4\pi\lambda(T_1-T_2)}{1/r_1-1/r_2}. \] 热阻 \[ R = \frac{1}{4\pi\lambda}\left(\frac{1}{r_1}-\frac{1}{r_2}\right). \]

要增加对流传热量（通常称为强化传热）可以通过增加温差、增加表面传热系数以及增加换热面积三种方法来达到，采用肋片（翅片）是增加换热面积的有效方法。下图展示了四种典型肋片结构

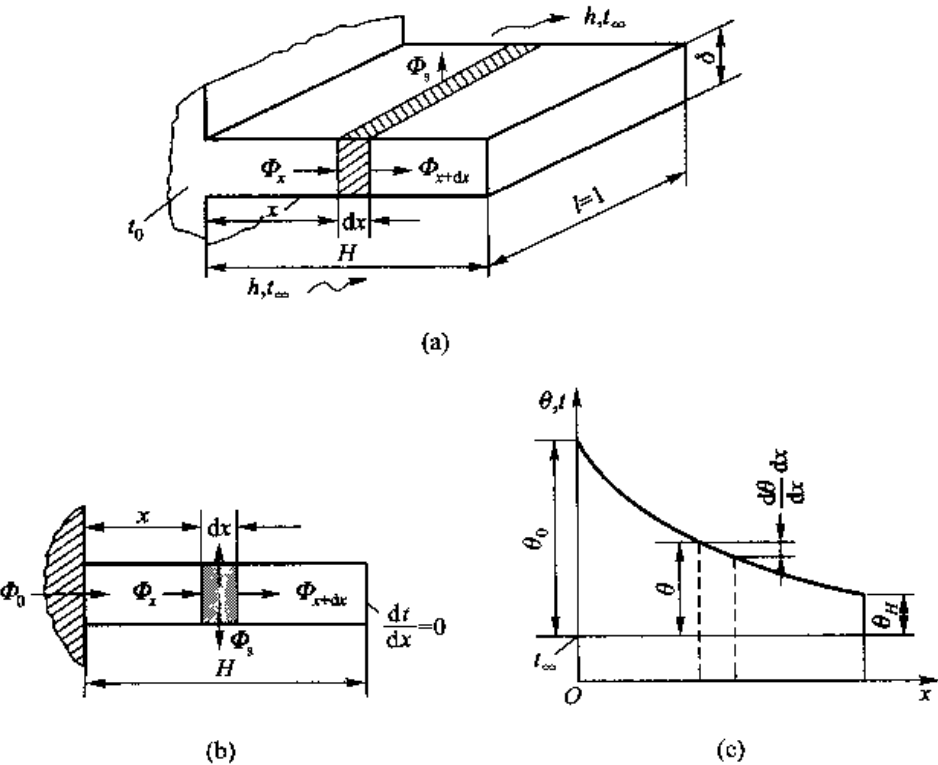
以下图肋片进行表面传热分析，肋片与基础表面相交处温度\(~T_0~\)已知，周围温度为\(~T_\infty\)，其中\(~T_0>T_\infty\)。

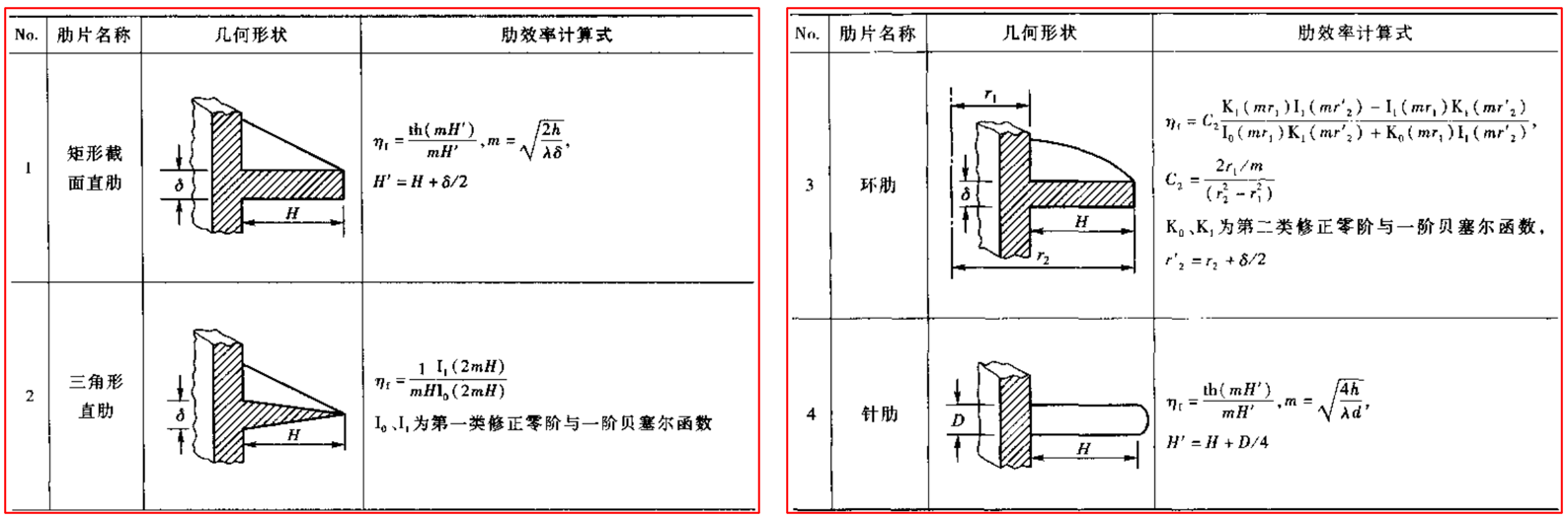
肋片中的温度场的数学方程为 \[ \frac{\mathrm{d}^2 T}{\mathrm{d}x^2} + \frac{\dot{\Phi}}{\lambda} = 0. \] 取长度为\(~\mathrm{d}x~\)的微元段分析，设参与换热的截面周长为\(~P\)，则表面的总散热量为 \[ \Phi_\text{s} = (P\mathrm{d}x)h(T-T_\infty), \] 相应的微元体积\(~A_\text{c}\mathrm{d}x\)，因而相应的折算源项为 \[ \dot{\Phi} = -\frac{\Phi_\text{s}}{A_\text{c}\mathrm{d}x}=-\frac{hP(T-T_\infty)}{A_\text{c}}. \]

因此有 \[ \frac{\mathrm{d}^2 T}{\mathrm{d}x^2} = \frac{hP(T-T_\infty)}{A_\text{c}}. \] 其相应的边界条件为 \[ x = 0, T = T_0; x = H, \frac{\mathrm{d}T}{\mathrm{d}x} = 0. \]

引入过余温度\(~\theta = T - T_\infty\)，令\(~m=\sqrt{hP/(\lambda A_\text{c})}\)，可得到过余温度的齐次方程和边界条件分别为 \[ \frac{\mathrm{d}^2 \theta}{\mathrm{d}x^2} = m^2\theta, \] 和 \[ \begin{aligned} x &= 0, \theta = \theta_0 = T_0 - T_\infty; \\ x &= H, \frac{\mathrm{d}\theta}{\mathrm{d}x} = 0. \end{aligned} \] 其解为 \[ \theta = \theta_0 \frac{\mathrm{e}^{mx}+\mathrm{e}^{2mH}\mathrm{e}^{-mx}}{1+\mathrm{e}^{2mH}} = \theta_0 \frac{\cosh \left[m(x-H)\right]}{\cosh(mH)}. \] 由肋片散入外界的全部热量都必须通过\(~x=0~\)处的肋根截面，此时热流量为 \[ \begin{aligned} \Phi_{x=0} &= -\lambda A_\text{c}\left( \frac{\mathrm{d}\theta}{\mathrm{d} x} \right)_{x=0} = -\lambda A_\text{c} \theta_0(-m) \frac{\sinh (mH)}{\cosh (mH)} \\ &= \lambda A_\text{c} \theta_0 m \tanh(mH) = \frac{hP}{m} \theta_0 \tanh(mH). \end{aligned} \]

为了表征肋片的散热的有效程度，引入肋效率（fin efficiency） \[ \eta_\text{f} = \frac{\text{实际散热量}}{\text{假设整个肋表面处于肋基温度下的热量}}, \] 则有 \[ \eta_\text{f} = \frac{ \frac{hP}{m} \theta_0 \tanh(mH)}{hPH\theta_0} = \frac{\tanh (mH)}{mH}. \]

下图展示了矩形界面直肋、三角形界面直肋、环肋和针肋

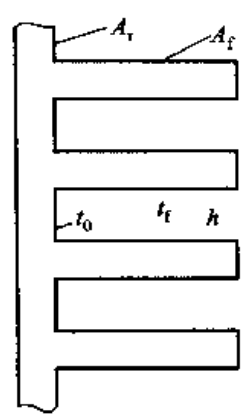
实际肋片总是成组地被采用地，如下图所示

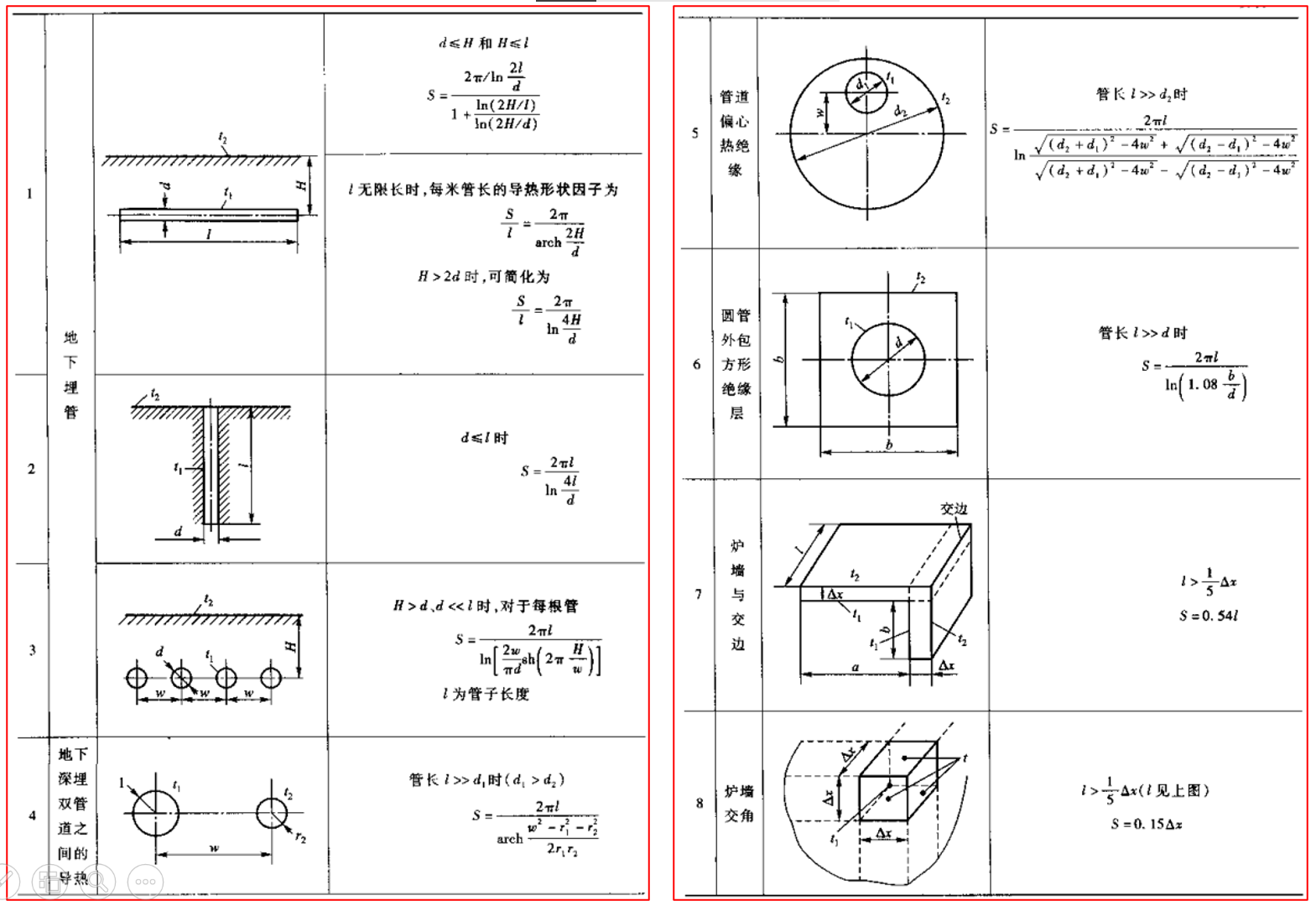
假设流体的温度为\(~T_\text{f}\)，流体与整个表面的表面传热系数为\(~h\)，肋片的表面积为\(~A_\text{f}\)，两个肋片之间的根部表面积为\(~A_\text{r}\)，根部温度为\(~T_0\)，则所有肋片与根部面积之和为\(~A_0 = A_\text{f} + A_\text{r}\)。计算该表面对流换热量时，以\(~T_0-T_\text{f}~\)为温差，则有： \[ \begin{aligned} \Phi &= A_\text{r} h (T_0 - T_\text{f}) + A_\text{f} \eta_\text{f}h(T_0-T_\text{f}) \\ &= h(T_0 - T_\text{f})(A_\text{r} + \eta_\text{f}A_\text{f}) = A_0\eta_0 h(T_0-T_\text{f}), \end{aligned} \] 其中 \[ \eta_0 = \frac{A_\text{r} + \eta_\text{f} A_\text{f}}{A_\text{r} + A_\text{f}} \] 称为肋面总效率（overall fin surface efficiency），显然肋片总效率高于肋片效率。

为了增加传热量，可知可以采用增加传热面积的方法，当会增加通过固体的导热热阻。增加肋片是否有利传热取决于导热热阻（\(\delta/\lambda\)）与表面对流传热阻力（\(1/h\)）之比。这两个数比值记为\(~Bi=h\delta/\lambda\)，称为毕渥数（Biot 数）。对于等截面的直肋，当\(~Bi\leq 0.25~\)时，加肋总是有利的。

肋片与管子之间的接触是否良好对于肋片作用发挥重要意义，实际上两个互相接触的固体表面，常常充满空气，热量将以导热方式穿过这种气隙层。这种情况与两固体表面真正完全接触相比，增加了附加的接触热阻。常见电子器件接触面处的空气间隙厚度大约在 1 ~ 25 µm 范围。在常规压力下，几个代表性的单位面积界面热阻如下：不锈钢/不锈钢 (2.2 ~ 5.88)×10-4 m2·K/W，铝/铝为 (0.833 ~ 4.55)×10-4 m2·K/W，不锈钢/铝为 (2.22 ~ 3.33)×10-4 m2·K/W，铜/铜为 (0.25 ~ 2.5)×10-4 m2·K/W。减小固体间接触热阻有：(1) 降低接触面粗糙度，(2) 增加接触面压力，(3) 使用硬度小的物体。

假设一大平壁具有均匀内热源\(~\dot{\Phi}\)，其两侧同时与温度为\(~T_\text{f}~\)的流体发生对流传热，表面传热系数为\(~h\)，壁厚为\(~2\delta\)，导热系数为\(~\lambda\)，则平壁内部温度分布为 \[ T = \frac{\dot{\Phi}}{2\lambda}(\delta^2 - x^2) + \frac{\dot{\Phi}\delta}{h} + T_\text{f}. \]

半径为\(~r_1~\)的圆柱体，具有均匀内热源\(~\dot{\Phi}\)，导热系数为\(~\lambda\)，外表面维持恒定温度\(~T_\text{f}\)，则圆柱体中温度分布为 \[ T = \frac{1}{4} \frac{\dot{\Phi}}{\lambda}(r_1^2-r^2) + T_\text{f}. \]

分离变量法（method of separation of variables）是傅里叶 19 世纪发展起来的。该方法具有以下限制：(1) 求解区域比较简单；(2) 边界条件比较简单；(3) 物体的热物性为常数。

随着计算机的发展,通过计算机获得导热问题的数值解的方法迅速发展。这时得到的并不是物体中温度场的函数形式，而只是相应于某个计算条件下物体中代表性地点上的温度值。尽管解的通用性不及分析解，但是由于可以获得分析方法难以得到的结果，并且实施方便，其应用日益广泛，将在第 4 章中予以介绍。

由于稳态导热温度场与导电物体中的电势场都要满足拉普拉斯方程，因此当两者的边界条件安排恰当时，从数学角度，两种场的解是一样的或者成比例的，这就导致通过比较容易测定的电势场来获得温度场的思想，这种方法称为模拟法（analog method）。

如果求解的目的在于获得物体所传导的热量，则当导热物体主要是由两个等温的边界组成时，可以采用下述形状因子法（shape factor method）。

两个等温面间导热热流量总是可以表示为统一形式： \[ \Phi = \lambda S(T_1 - T_2), \] 其中形状因子\(~S~\)与导热物体的形状及大小有关。下表列举了一些形状因子的表达式

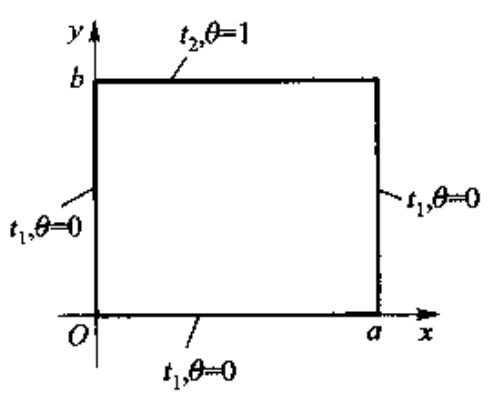
一个二维矩形物体三个边界温度均为\(~T_1\)，第四个边界温度为\(~T_2\)，物体无内热源，导热系数为常数，现要确定物体中的温度分布。

控制方程和边界条件分别写作 \[ \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} =0 \] 和 \[ \begin{aligned} T(0,y) = T_1, T(a,y) = T_1, \\ T(x,0) = T_1, T(x,b) = T_2. \end{aligned} \] 引入无量纲过余温度 \[ \Theta = \frac{T - T_1}{T_2 - T_1}, \] 则有 \[ \frac{\partial^2 \Theta}{\partial x^2} + \frac{\partial^2 \Theta}{\partial y^2} =0 \] 和 \[ \begin{aligned} \Theta(0,y) = 0, T(a,y) = 0, \\ \Theta(x,0) = 0, T(x,b) = 1. \end{aligned} \]

该方程的边界条件是齐次的，设\(~\Theta(x,y) = X(x)\cdot Y(y)\)，则方程可化为关于\(~X~\)和\(~Y~\)的两个常微分方程。为使通解满足边界条件，引入傅里叶级数，可以得出如下分析解： \[ \Theta(x,y) = \frac{2}{\pi} \sum_{n=1}^\infty \frac{(-1)^{n+1}+1}{n} \sin\frac{n\pi x}{a}\frac{\sinh(n\pi y/a)}{\sinh(n\pi b/a)}. \]

对于三种典型的几何形状在常物性、无内热源、第一类边界条件下的温度场、热流量计算式、热阻以及肋片导热分析解如下表所示