广义混合变分不等式的weak

余 静， 夏福全

（四川师范大学数学科学学院，四川成都610066）

本文总假设Rn为欧式空间，〈·，·〉和‖·‖分别表示Rn的标准内积和l2范数.

设W⊆Rn是非空闭凸子集，θ：Rn→R∪｛＋∞｝是下半连续凸函数，F：Rn→2Rn是集值映射.本文所研究的广义混合变分不等式问题（简记为 GMVIP）为：求 w*∈W，y*∈F（w*），使得

本文总假设广义混合变分不等式问题的解集W*≠∅且 dom（θ）⊂W，其中

当集值映射F退化为单值映射F：Rn→Rn时，问题（1）退化为下列的一般混合变分不等式问题（简记为 MVIP）：求 x*∈W，使得

当θ：Rn→R∪｛＋∞｝为集合W的指示函数时，问题（1）退化为下列的广义变分不等式问题（简记为 GVIP）：求 x*∈W，y*∈F（x*），使得

Huang等［1］在Banach空间T中给出了一般混合变分不等式问题（2）的解集X*所满足的weaksharp 条件：存在 α ＞0，ε∈（0，1），使得

其中，W⊆T是非空闭凸子集，BT*是T的对偶空间T*中的单位闭球，F：T→T*是单值映射，g：T→R是下半连续凸函数，对是集值映射，其定义为

TW（x*）称为闭凸集 W在点 x*处的切锥，其定义为：

NX*（x*）称为集合X*在点x*处的法锥，其定义为

显然，

Huang等［1］利用与问题（2）相关的间隙函数，给出了weak-sharp条件（4）成立的等价刻画：存在 τ＞0，使得

其中，dist（x，X*）表示点 x到解集 X*的距离，其定义为：

h（x）表示与问题（2）相关的间隙函数，其定义为：

另一方面，Xiong等［2］在Rn空间中给出了广义变分不等式问题（3）的解集 S0所满足的weaksharp条件：存在α＞0，使得

其中，W⊆Rn是非空闭凸子集，B是Rn空间中的单位闭球，G：Rn→2Rn的集值映射，其定义为：

显然，对∀x∈Rn，G（x）⊆F（x）.

进一步，Xiong等［2］给出了 weak-sharp条件（5）成立的等价刻画：存在α＞0，使得

其中，δS（z）称为集合S的支撑函数，其定义为：

显然

对非空子集A，B⊆Rn有

最后，Xiong等［2］在GVIP问题的解集 S0满足 weak-sharp条件之下，获得了GVIP问题的任意迭代算法有限收敛的等价条件.

虽然Huang等［1］获得了一般混合变分不等式MVIP问题的解集X*满足weak-sharp条件的等价刻画，但是Huang等［1］并没有通过 weak-sharp条件获得MVIP问题解的任意迭代算法有限收敛的等价条件.而Xiong等［2］不仅获得了广义变分不等式GVIP问题的解集S0满足weak-sharp条件的等价刻画，同时通过GVIP解集满足weak-sharp条件的假设之下，获得求解GVIP问题解的任意迭代算法有限收敛的等价条件.本文将结合文献［1-2］中的方法，研究广义混合变分不等式GMVIP问题的解集W*满足 weak-sharp条件的等价刻画，并在GMVIP问题解集满足weak-sharp条件的假设之下，获得GMVIP问题解的任意迭代算法有限收敛的等价条件.最后，本文以广义混合变分不等式GMVIP问题的超投影近似点算法为特例，在一定的条件下，获得该算法的有限收敛性.

设非空集合 D⊆Rn，x∈Rn，如果

则称dist（x，D）为点 x到集合 D 的距离.如果

则称PD（x）为点x在集合D上的投影.显然，如果D是非空闭凸集，则PD（x）是单点集.

下面给出一个重要的投影性质：

显然，由（9）式有

下面给出一些定义及引理.

定义 1.1［3］设 F：Rn→2Rn是集值映射，如果对任意 x，y∈Rn，u∈F（x），v∈F（y），均有

则称集值映射F在Rn上单调.

定义 1.2［4］设 f：Rn→R，x∈Rn，若对任意收敛于x的点列｛xk｝⊆Rn均有

则称函数f：Rn→R在x处下半连续.如果函数f在Rn上每一点均下半连续，则称f在Rn上下半连续.

定义 1.3［4］设 θ：Rn→R，x∈Rn，如果

则称∂θ（x）为函数θ在x处的次微分.

定义 1.4［5］设｛Ck｝k∈N是Rn的非空子集序列，则｛Ck｝k∈N的内极限定义为

其中，N∞：＝｛N⊆N：N＼N 有限｝，N是自然数集表示序列按指标集N收敛.显然，如果Ck：＝｛xk｝，则内极限就等同于极限.

引理1.5设W⊆Rn是非空闭凸子集，w∈W.则对∀z∈NW（w）有

其中，TW（w）为闭凸集W在点w处的切锥.

证明由W是非空闭凸子集，可知TW（w）是非空闭凸锥且 NW（w）＝［TW（w）］◦.由 z∈NW（w），有 z∈［TW（w）］◦，则对∀y∈TW（w），有〈z，y〉≤0.因此 PTW（w）（z）＝0.

显然问题（1）等价于：求w*∈W，使得

由（11）式可知，存在 y*∈F（w*），z*∈∂θ（w*），使得

由（12）式及引理1.5 可知

引理 1.6［4］设 Ai⊆Rn（i＝1，2，…，m）是非空闭凸锥，则

引理 1.7［6］设 A⊆Rn，B⊆Rn，A、B 均为非空闭凸子集.则A⊆B当且仅当

引理 1.8［2］设 W⊆Rn是非空闭凸子集.w∈W，y∈Rn.则

首先本文给出GMVIP问题的解集W*满足的weak-sharp条件：存在α＞0，使得

其中，映射G由（6）式定义.

如果GMVIP问题（1）中的集值映射F退化为单值映射 F：Rn→Rn，则 GMVIP 问题（1）就退化为MVIP问题.此时，weak-sharp条件（1）就退化为weak-sharp条件（4）.如果 GMVIP 问题（1）中的函数θ退化为集合W的指示函数，则GMVIP问题（1）就退化为GVIP问题.此时，weak-sharp条件（14）就退化为weak-sharp条件（5）.

首先给出下列命题.

命题2.1下面等式恒成立：

（i）［TW（w*）∩NW*（w*）］◦＝cl conv（NW（w*）∪TW*（w*））；

（ii）对∀z∈Rn有

证明（i）由 W⊆Rn是非空闭凸集，可知TW（w*）是非空闭凸锥.而 NW*（w*）也是非空闭凸锥，则

由引理1.6可知结论成立.

（ii）设 z∈Rn，则

其中，上式中的第一个等式是由（i）获得，第二个等式是由（7）式获得，第三个等式是由（8）式获得.

命题 2.2［2］设 W⊆Rn是非空闭凸子集，F：Rn→2Rn是集值映射，G：Rn→2Rn是集值映射，则

（i）如果F在W上极大单调，则G在W*上是凸值；

（ii）如果F在W上是紧值，则G在W*上是紧值.

下面给出问题（1）的解集W*满足（14）式的一个等价条件.

定理2.3设G在W*上是紧凸值，则问题（1）的解集W*满足weak-sharp条件当且仅当存在α＞0，使得

证明设G在W*上是紧凸值，w*∈W*，则G（w*）是紧凸集.显然，αB 是紧凸集，∂θ（w*）是闭凸集，又由［TW（w*）∩NW*（w*）］◦是闭凸集可知G（w*）＋∂θ（w*）＋［TW（w*）∩NW*（w*）］◦是闭凸集.设解集W*满足weak-sharp条件，则由（14）式可知，存在α＞0，使得对∀w*∈W*有

因此，对∀z∈Rn有

式中的第一个不等式是由W*满足（17）式及引理1.7 获得，最后一个等式是由命题 2.1 中的（ii）获得.若存在 α ＞0，对∀w*∈W*，∀z∈Rn，有（16）式成立.则由（18）式可得

由（19）式及引理1.7 可得

下面将在GMVIP问题（1）解集满足weaksharp条件的假设之下，获得GMVIP问题（1）解的任意迭代算法有限收敛的等价条件.

定理 3.1设 W⊆Rn是非空闭凸子集，｛wk｝⊆W.F：Rn→2Rn是集值映射，θ：Rn→R∪｛＋ ∞ ｝为真凸下半连续函数.若对于充分大的k，wk∈W*，则存在 yk∈F（wk），zk∈∂θ（wk），使得

证明设存在 k0＞0，当 k≥k0时，有 wk∈W*.则当 k≥k0时，由（11）式有

由（21）式可知，存在 yk∈F（wk），zk∈∂θ（wk），使得

由（22）式及引理1.5 有

因此，（20）式成立.

定理3.2设 W⊆Rn是非空闭凸子集.F：Rn→2Rn是单调集值映射，θ：Rn→R∪｛＋ ∞ ｝为真凸下半连续函数.问题（1）的解集W*是非空闭凸子集且满足（14）式.｛wk｝⊆W是任意迭代算法产生的序列.则对于充分大的k，wk∈W*当且仅当

其中，

证明设存在 k0＞0，当 k≥k0时，有 wk∈W*.则当 k≥k0时，由（11）式可得

由（24）式可知，存在 yk∈F（wk），zk∈∂θ（wk），使得

由（25）式及引理1.5 可知，当 k≥k0时，有

令 N：＝｛k0＋1，k0＋2，…｝，显然 N∈N∞，又

及

由（27）和（28）式可得

设（23）式成立.假设对∀K∈N，存在 k≥K，使得 wk≥W*.也即存在序列｛wk｝k∈K⊆｛wk｝，K⊆N，使得wk≥W*.由（23）式可知，存在 N∈N∞，yk∈F（wk），zk∈∂θ（wk），k∈N 使得

令 Z＝K∩N，由（29）式有

由W*是非空闭凸子集，则对∀wk（k∈Z），存在唯一 uk∈W*，使得

由（31）式可得

则对∀k∈Z，有

及

由W*满足（14）式，则存在α＞0，使得对∀k∈Z有

使得

因此，对∀k∈Z有

式中的第二个等式是由（35）式获得，第一个不等式是由（32）式及

获得，第二个不等式是由F的单调性及∂θ的单调性获得，最后一个不等式是由（33）式及

获得，最后一个等式是由引理1.8获得.由于

因此，由（36）式可得 α≤0，与 α ＞0矛盾.故结论成立.

如果GMVIP问题（1）中的集值映射F退化为单值映射 F：Rn→Rn，则 GMVIP 问题（1）就退化为MVIP问题.由（4）式可知，MVIP问题的解集W*满足的weak-sharp条件为：

从而，由定理3.2可得如下推论：

推论 3.3设 W⊆Rn是非空闭凸子集.F：Rn→Rn是单调单值映射，θ：Rn→R∪｛＋∞｝为真凸下半连续函数.MVIP问题的解集W*是非空闭凸子集且满足（37）式.｛wk｝⊆W是任意迭代算法产生的序列.则对于充分大的k，wk∈W*当且仅当

其中

3.1 超投影近似点算法的有限收敛显然问题（1）等价于：求 w*∈W，使得

令

则问题（1）等价于：求 w*∈W，使得

接下来，本文将根据Solodov等［7］提出的求解极大单调包含问题（41）的超投影近似点算法，给出求解GMVIP 问题（1）的超投影近似点算法 3.1.1，并运用定理3.2证明此算法在满足一定条件下有限收敛.

算法 3.1.1第一步：任给 z0∈Rn，σ∈［0，1），得到 zk.

第二步：任给 μk＞0，求 wk∈Rn，使得

其中，mk∈F（wk），hk∈NW（wk），rk∈∂θ（wk），εk满足

第三步：如果 mk＋hk＋rk＝0或 wk＝zk，停止迭代.否则

第四步：令k＝k＋1，回到第二步.

对于算法3.1.1，假设下面的条件成立：

（i）W*≠∅；

（ii）F：Rn→2Rn为极大单调映射；

（iii）W⊆dom F，ri（dom F）∩ri（W）∩W*≠∅.假设（i）～（iii）保证了映射 A＝F ＋NW＋∂θ是极大单调的.

定理 3.1.2［7］设｛zk｝是由算法 3.1.1 获得的序列，则

（a）｛zk｝有界；

（b）若参数序列｛μk｝满足 μk≤μ ＜ ∞，∀k＝0，1，2，…，则收敛到W*中的点.

定理 3.1.3设 W⊆Rn是非空闭凸子集，θ：Rn→R∪｛＋∞｝为真凸下半连续函数.GMVIP问题的解集 W*是非空闭凸子集且满足（14）式.｛wk｝⊆W 是算法 3.1.1 产生的序列.假设（i）～（iii）成立.则对于充分大的 k，wk∈W*.

证明由定理 3.1.2的（b）可知，存在≥z∈W*，使得

由（a）可知

则存在N∈N∞使得

由 W 是非空闭凸集，则对∀k∈N，TW（wk），NW（wk）均为非空闭凸锥.由 Moreau分解定理，对mk∈F（wk），rk∈∂θ（wk）有

因此，对 hk∈NW（wk）（k∈N）及（45）式，有

由（44）和（46）式可得

又

因此，由定义1.4可得

由定理3.2可知结论成立.

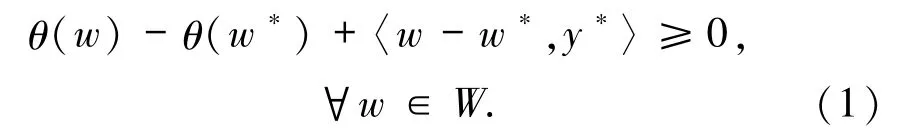
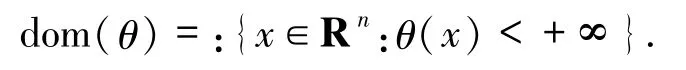
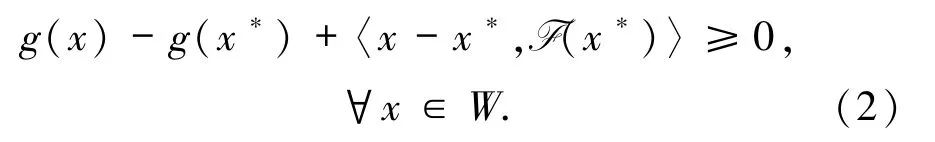
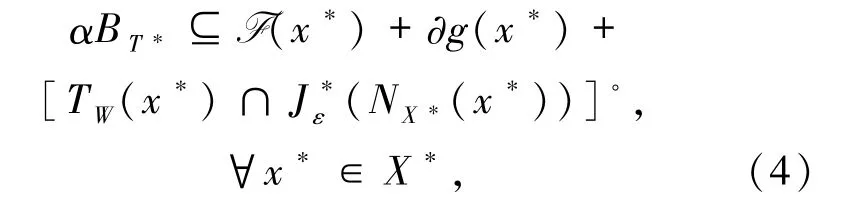
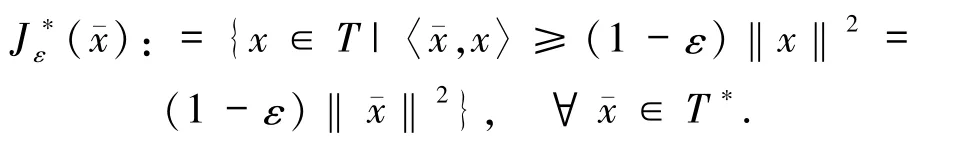
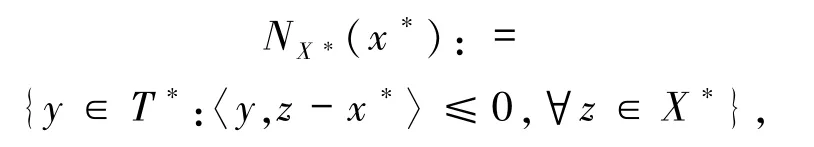
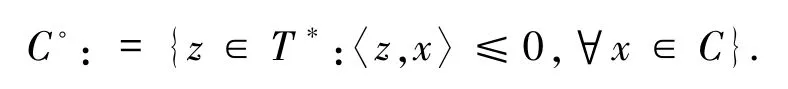
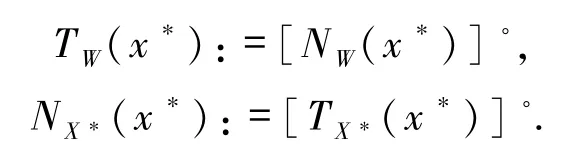
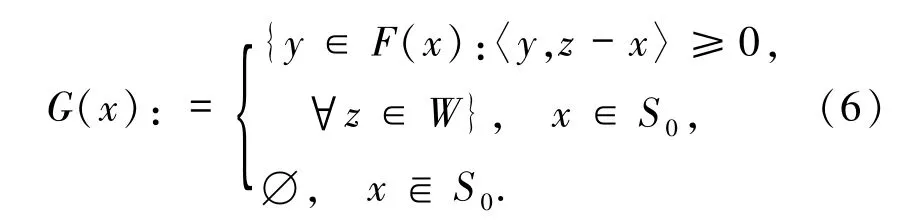
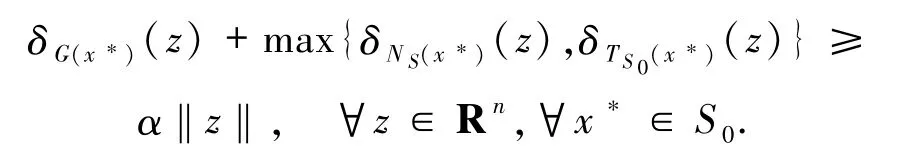
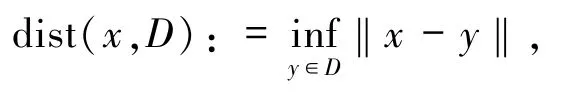
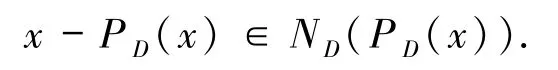
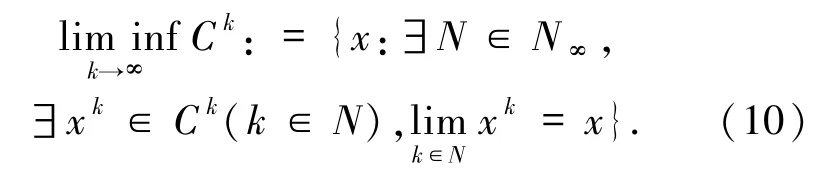
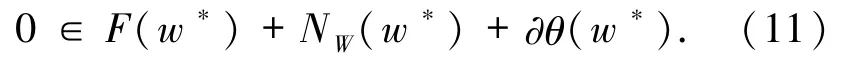
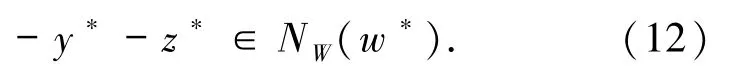
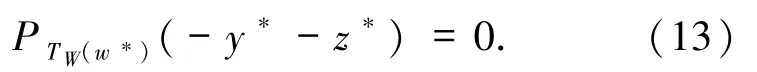
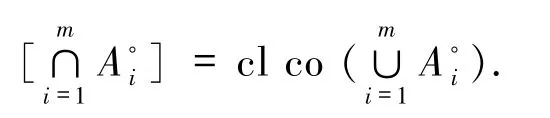
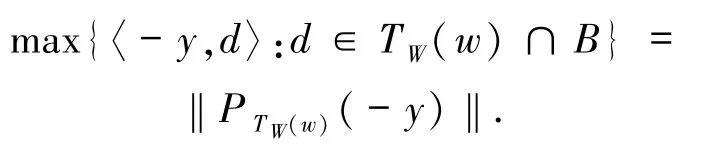
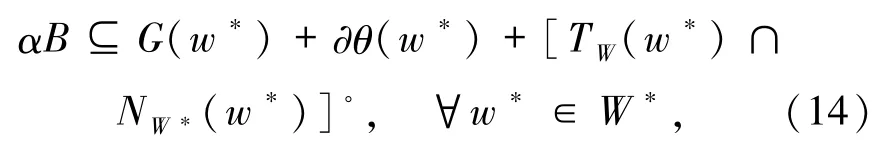
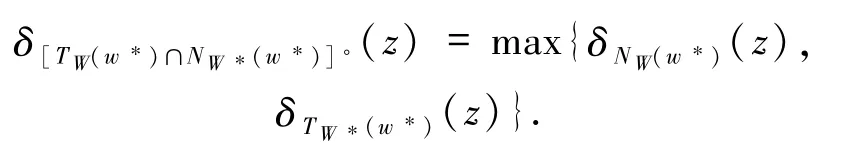
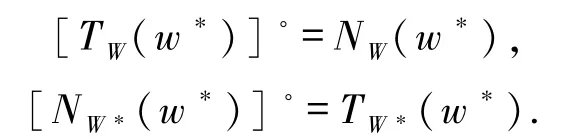
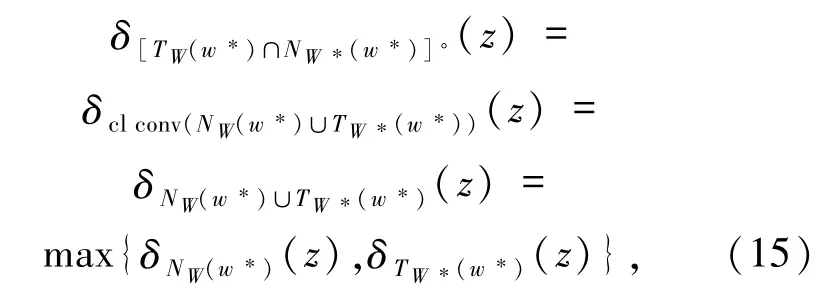
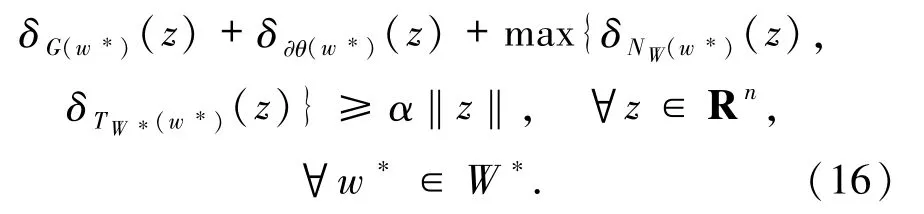
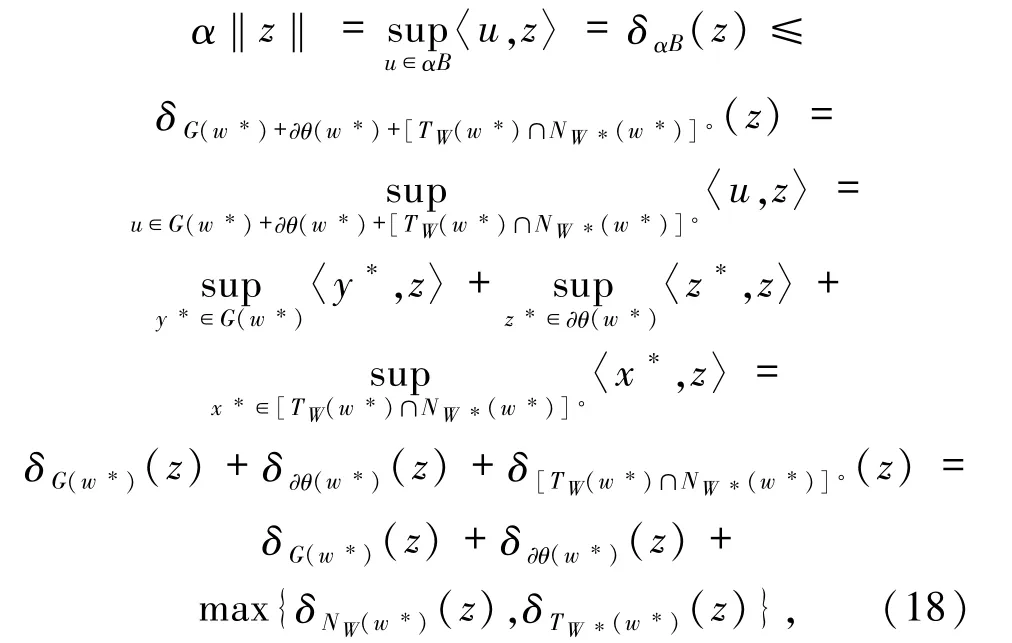
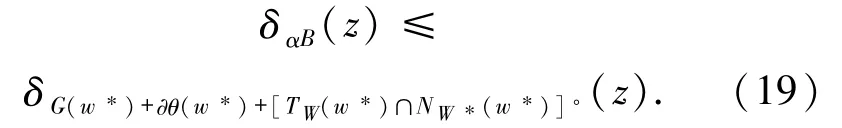
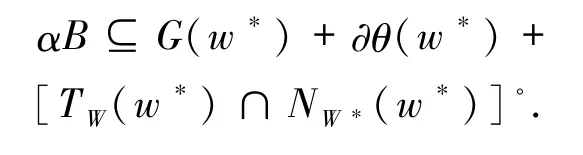
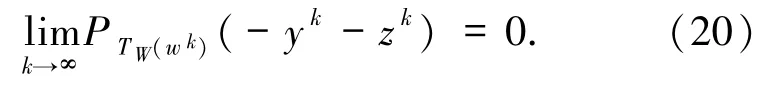
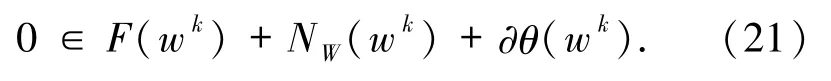
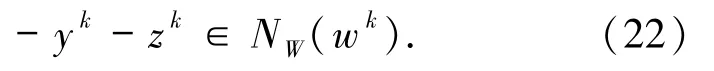
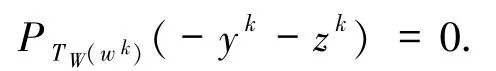
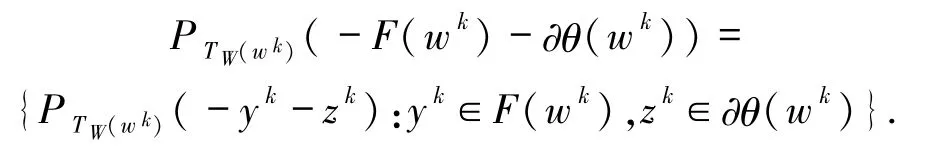
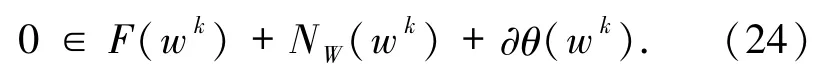
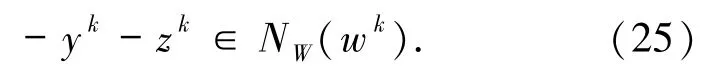
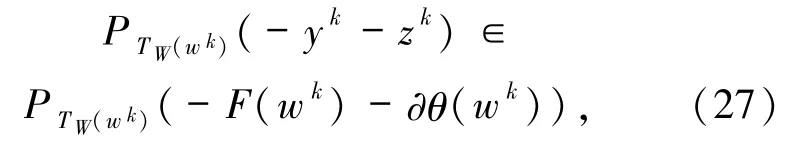
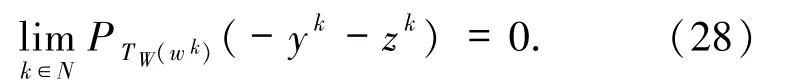
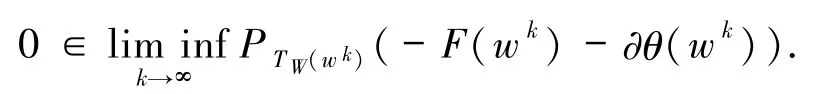
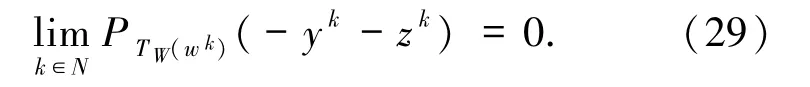
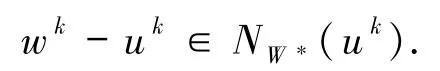
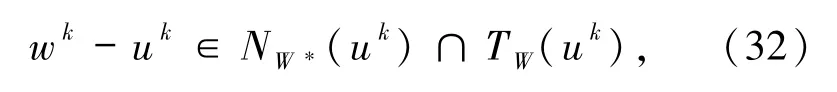
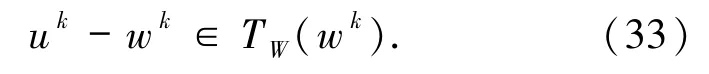
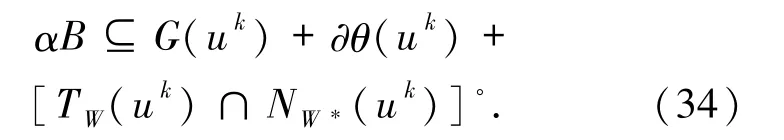
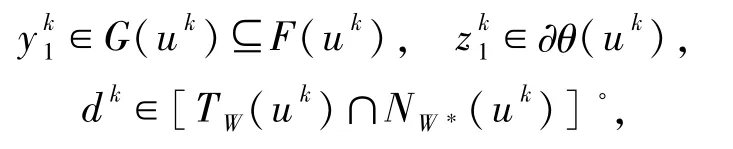
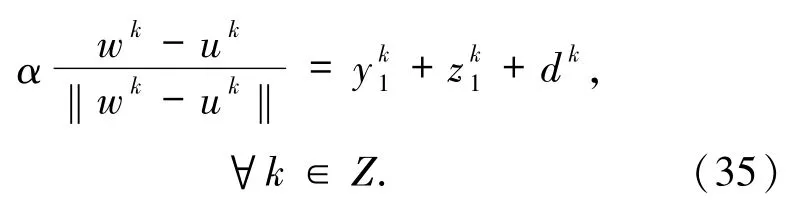
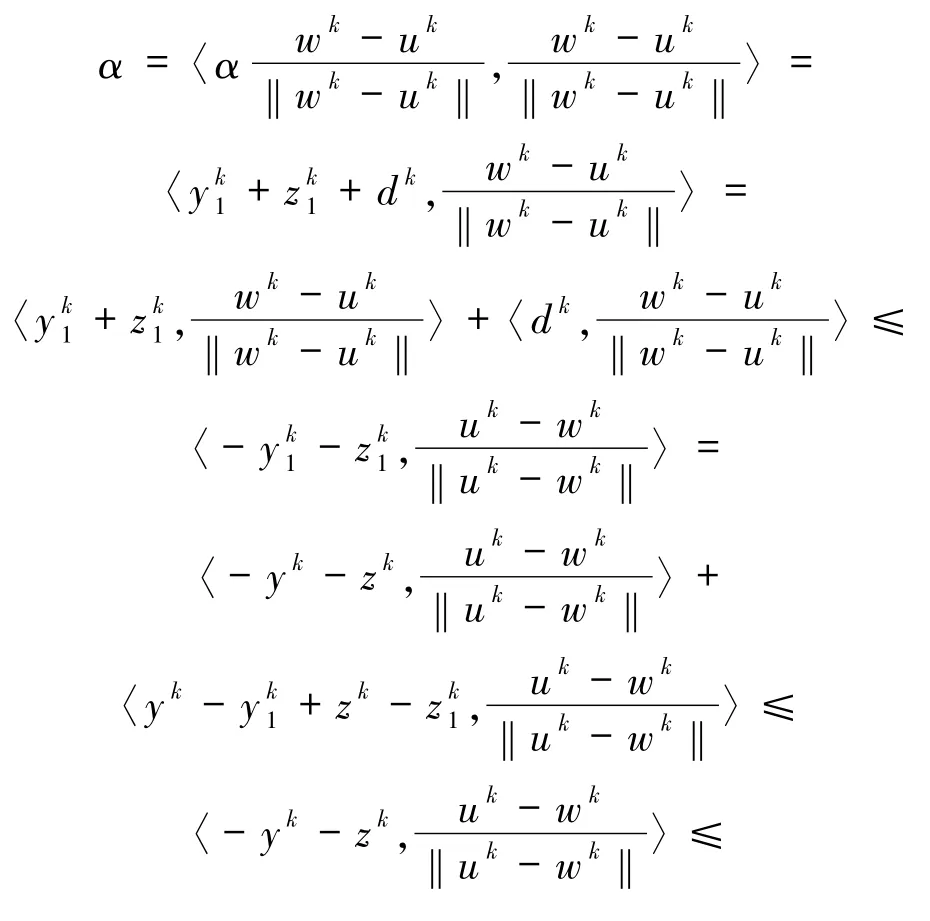
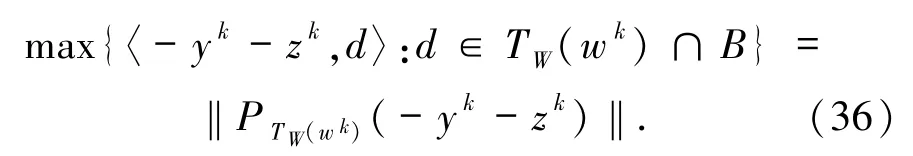
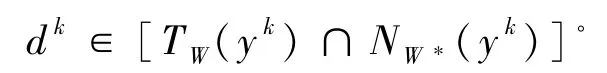
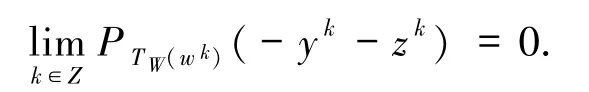
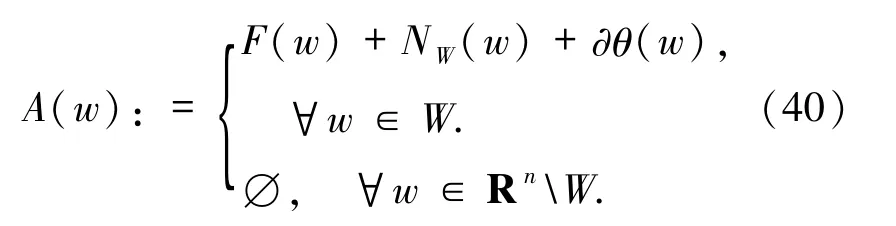
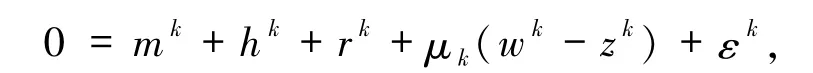
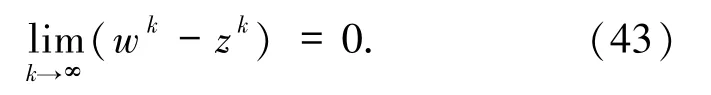
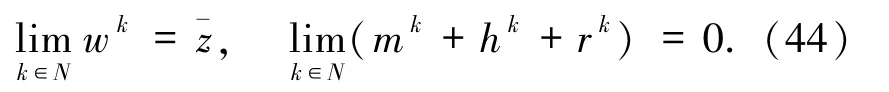
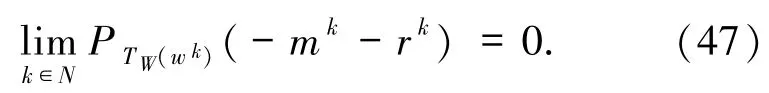
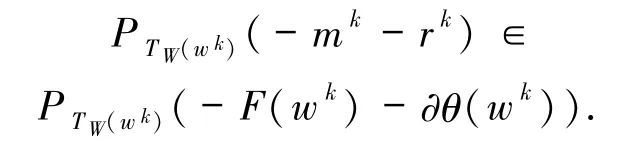
四川师范大学学报（自然科学版）2020年5期