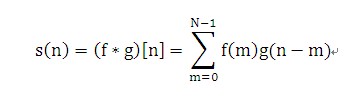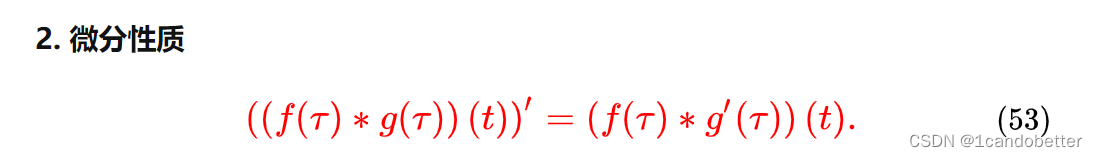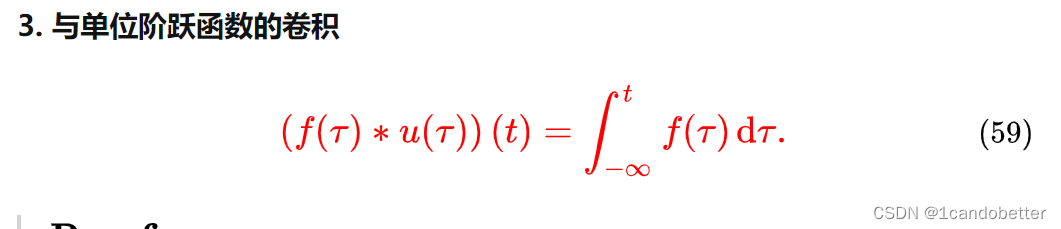数（3）相关运算和卷积运算

目录

相关运算

卷积运算

连续信号 

离散信号 

 卷积性质

 卷积定理

（参考其他多篇博客，学习自用，侵删）

 相关运算是两个序列的相似性比较的一种数学运算。

公式里面的序列，可能是实数，可能是复数（无线通信信号处理通常都是复数域进行）。

两个相关函数都是对相关性，即相似性的度量。如果进行归一化，会看的更清楚。

      相关运算从线性空间的角度看其实是内积运算，而两个向量的内积在线性空间中表示一个向量向另一个向量的投影，表示两个向量的相似程度，所以相关运算就体现了这种相似程度。

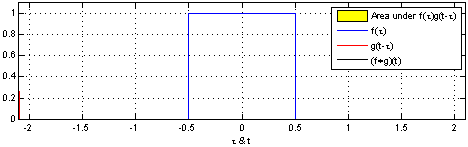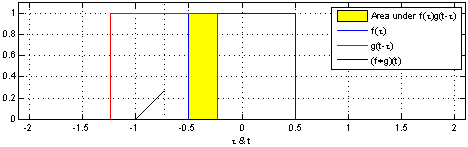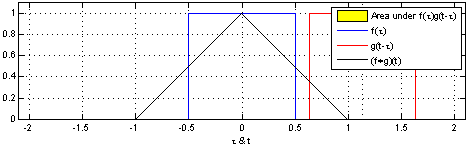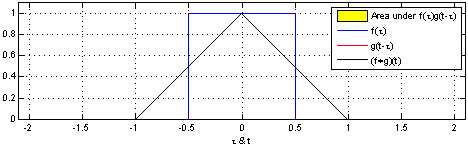
互相关函数和卷积运算类似，也是两个序列滑动相乘，但是区别在于：互相关的两个序列都不翻转，直接滑动相乘，求和；卷积的其中一个序列需要先翻转，然后滑动相乘，求和。所以，f(t)和g(t) 做相关等于 f*(-t) 与 g(t) 做卷积。

卷积与相关关系：两图形互相关运算等效于两图像之一先折叠后，与另一图形进行卷积运算。

下面可以进入核心内容——卷积了！ 如果你每天都到地下去打台球，那么老板每天都要扇你一巴掌，不过当老板打你一巴掌后，你5分钟就消肿了，所以时间长了，你甚至就适应这种生活了……如果有一天，老板忍无可忍，以0.5秒的间隔开始不间断的扇你的过程，这样问题就来了，第一次扇你鼓起来的包还没消肿，第二个巴掌就来了，你脸上的包就可能鼓起来两倍高，老板不断扇你，脉冲不断作用在你脸上，效果不断叠加了，这样这些效果就可以求和了，结果就是你脸上的包的高度随时间变化的一个函数了（注意理解）；如果老板再狠一点，频率越来越高，以至于你都辨别不清时间间隔了，那么，求和就变成积分了。可以这样理解，在这个过程中的某一固定的时刻，你的脸上的包的鼓起程度和什么有关呢？和之前每次打你都有关！但是各次的贡献是不一样的，越早打的巴掌，贡献越小，所以这就是说，某一时刻的输出是之前很多次输入乘以各自的衰减系数之后的叠加而形成某一点的输出，然后再把不同时刻的输出点放在一起，形成一个函数，这就是卷积，卷积之后的函数就是你脸上的包的大小随时间变化的函数。本来你的包几分钟就可以消肿，可是如果连续打，几个小时也消不了肿了，这难道不是一种平滑过程么？反映到剑桥大学的公式上，f(a)就是第a个巴掌，g(x-a)就是第a个巴掌在x时刻的作用程度，乘起来再叠加就ok。

卷积的含义：狭义的物理概念是激励信号（如f(t)）通过特性为g(t)（系统冲激响应）响应的结果。广义而言，是两个函数波形相互影响过程的总和，其一折叠后，两者从首尾相接相互扫描（且相乘）过程的连续和。

卷积步骤：开始卷积前，先将变量t变，且决定其中一波形折叠后并移位t，移至固定波形左侧，首位相接，然后开始卷积------随参变量t增加，二图像逐渐重叠（相乘积分）直至扫描结束。

离散信号f(n),g(n)的定义如下：

N-----为信号f(n)的长度

s(n)----为卷积结果序列,长度为len(f(n))+len(g(n))-1

例：

f(n) = [1 2 3]; g(n) = [2 3 1];

s(0) = f(0)g(0-0) + f(1)g(0-1)+f(2)g(0-2)

= 1*2 + 2*0 + 3*0 =2

s(1) = f(0)g(1-0) + f(1)g(1-1) + f(2)g(1-2)

   = 1*3 + 2*2 + 3*0 = 7

s(2) = f(0)g(2-0) + f(1)g(2-1) + f(2)g(2-2)

=1*1 + 2*3 + 3*2=13

s(3) = f(0)g(3-0) + f(1)g(3-1) + f(2)g(3-2)

=1*0 + 2*1 + 3*3=11

s(4) = f(0)g(4-0) + f(1)g(4-1) + f(2)g(4-2)

=1*0 + 2*0 + 3*1=3

最终结果为:

     s(n) = [2 7 13 11 3]

上述计算图示如下：

在数学里我们知道f(-x)的图像是f(x)对y轴的反转

     g(-m)就是把g(m)的序列反转，g(n-m)的意义是把g(-m)平移的n点：

如上图g(m)在信号处理中通常叫做滤波器或掩码，卷积相当于掩码g(m)反转后在信号f(n)上平移求和。Matlab计算卷积的函数为conv,

>> A = [1 2 3];

B = [2,3,1];

convD = conv(A,B)

convD =

     2     7    13    11     3

相应的二维卷积定义如下：

 卷积定理是傅立叶变换满足的一个重要性质。卷积定理指出，函数卷积的傅立叶变换是函数傅立叶变换的乘积。具体分为时域卷积定理和频域卷积定理