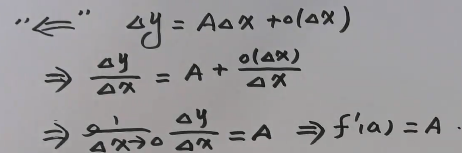导数与微分

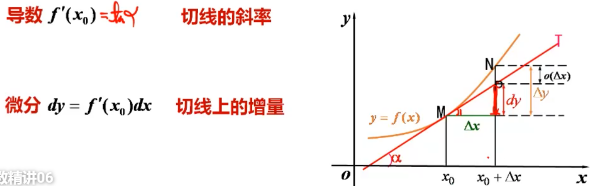
增量

​ 若f(x)在点x0的某个领域有定义，称 Δ y = f ( x 0 + Δ x ) − f ( x 0 ) \Delta y = {f ( x _ { 0 } + \Delta x )} - {f ( x _ { 0 } )} Δy=f(x0​+Δx)−f(x0​)为函数y=f(x)在x0处的增量。

导数（导数就是一个特殊的极限）

​ 导数的定义是Δx趋于0，而不能等于0，如sin(1/x)就有等于0的点，不能作为导数定义式。

（命题点）导数的等价定义：（极限存在才能=f’(a)，未说明则不能=） f ′ ( a ) = lim ⁡ x → 0 f ( a + x ) − f ( a ) a + x − x = lim ⁡ h → 0 f ( a + h ) − f ( a ) h = lim ⁡ x → a f ( x ) − f ( a ) x − a \begin{align} f'(a) & =\lim_{x \rightarrow 0}\frac{f(a+x)-f(a)}{a+x-x} \\ & = \lim_{h \rightarrow 0}\frac{f(a+h)-f(a)}{h} \\ & = \lim_{x \rightarrow a}\frac{f(x)-f(a)}{x-a} \end{align} f′(a)​=x→0lim​a+x−xf(a+x)−f(a)​=h→0lim​hf(a+h)−f(a)​=x→alim​x−af(x)−f(a)​​​

​ 导数的定义是一个定点一个动点，而不能两个都是动点，如 f ( 2 x ) − f ( x ) 、 f ( x + k ) − f ( x − k ) f(2x)-f(x)、f(x+k)-f(x-k) f(2x)−f(x)、f(x+k)−f(x−k)都是两个动点，错误

可导的充要条件

​ 函数f(x)在x=x0处可导的充要条件是左右导数存在且相等。若题目说明可导，则极限是存在的。

注解

可微

增量：Δy = f(x0+Δx) - f(x0)。

​ 若 Δ y = f ( x 0 + Δ x ) − f ( x 0 ) = A Δ x + o ( Δ x ) \Delta y = {f ( x _ { 0 } + \Delta x )} - {f ( x _ { 0 } )} = A \Delta x + o ( \Delta x ) Δy=f(x0​+Δx)−f(x0​)=AΔx+o(Δx)，其中A是常数，则称y=f(x)在x=x0处可微。其中AΔx称为y=f(x)在x=x0处的微分，记为dy|x=x0= AΔx = Adx Δ y = f ( x 0 + Δ x ) − f ( x 0 ) = A Δ x + o ( Δ x ) = d y ∣ x = x 0 + o ( Δ x ) = A d x + o ( Δ x ) = d f ( x 0 ) + o ( Δ x ) = f ′ ( x 0 ) d x + o ( Δ x ) \begin{align} Δy & = f(x_0+Δx) - f(x_0) \\ & = AΔx + o(Δx) \\ & = dy|_{x=x_0} + o(Δx) \\ & = Adx + o(Δx) \\ & = df(x_0) + o(Δx)\\ & = f'(x_0)dx + o(Δx)\\ \end{align} Δy​=f(x0​+Δx)−f(x0​)=AΔx+o(Δx)=dy∣x=x0​​+o(Δx)=Adx+o(Δx)=df(x0​)+o(Δx)=f′(x0​)dx+o(Δx)​​

其他补充

导数与微分的关系（导数 不等于 微分）

【例题】2013数一

​ 连续不一定可导，可导必连续。连续函数某一点可能是尖的，那就不可导。经典反例f(x)=|x|在x=0这点。

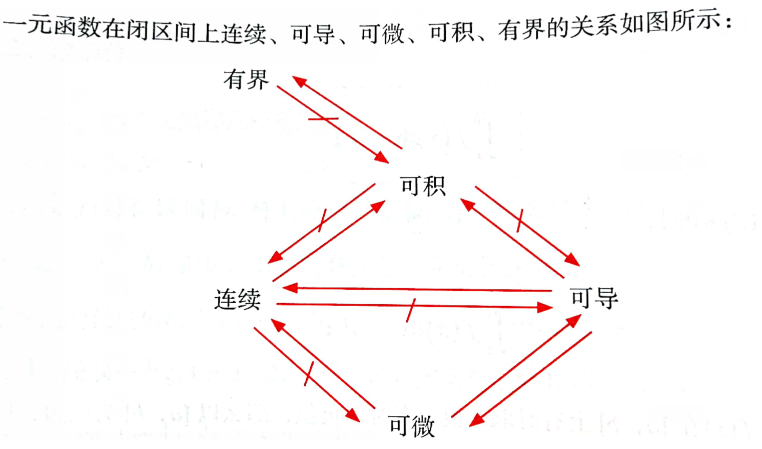
可微 > = 可导 > 连续 > 可积 > 有界

证明 一阶可导 == 可微

导->微 ∵ lim ⁡ Δ x → 0 Δ y Δ x = f ′ ( a ) ∴ Δ y Δ x = f ′ ( a ) + α   ( α → 0 , Δ x → 0 ) ∴ Δ y = f ′ ( a ) Δ x + α Δ x ∵ lim ⁡ Δ x → 0 α Δ x Δ x = 0 ∴ α Δ x = o ( Δ x ) ∴ Δ y = f ′ ( a ) Δ x + o ( Δ x ) \begin{aligned} & \because \lim_{Δx \rightarrow0}\frac{\Delta y}{\Delta x} = f'(a) \\ & \therefore \frac{\Delta y}{\Delta x} = f'(a) + \alpha \ (\alpha \rightarrow0,\Delta x \rightarrow0) \\ & \therefore \Delta y = f'(a) \Delta x + \alpha \Delta x \\ & \because \lim_{\Delta x \rightarrow 0} \frac{\alpha \Delta x}{\Delta x} = 0 \\ & \therefore \alpha \Delta x = o(\Delta x) \\ & \therefore \Delta y = f'(a)\Delta x + o(\Delta x) \end{aligned} ​∵Δx→0lim​ΔxΔy​=f′(a)∴ΔxΔy​=f′(a)+α (α→0,Δx→0)∴Δy=f′(a)Δx+αΔx∵Δx→0lim​ΔxαΔx​=0∴αΔx=o(Δx)∴Δy=f′(a)Δx+o(Δx)​

微->导

f(x)可导不能得出f’(x)可导，不能得出f’(x)连续、不能得出lim f’(x)存在

​ 可导函数，导数不为0，根据介值定理知导数恒大于0或恒小于0，那么该函数单调。

证明可导性的一般步骤：先看连续不连续，不连续则必不可导；再看左右导数是否存在且相等，等则可导。注意：左右导数存在且相等，在x0点也未必可导，必须要加上连续这一条件，因为可能是跳跃间断点。

绝对值的可导性

​ 设函数f(x)在x=a处可导，则|f(x)|在x=a处的可导性如下：

若 f(a) !=0，则|f(x)|在x = a处可导

若 f(a) = 0，则当f’(a) = 0 时，|f(x)|在x=a可导；当f’(a) != 0时，|f(x)|在x = a处不可导

例子：f(x) = x 与 |f(x)| 在x = 0处的可导性

​ 一般只有一阶可导(只能保证一阶连续不能保证二阶连续)时不能洛（处处可导也不行），因为洛了之后有f’(x)，要确保lim f’(x)是存在的(但一阶可导不能得出lim f’(x)存在)；同理若二阶可导则可以洛一次，除非lim f’'(x)存在。即若n阶可导，至多导到n-1阶；若n阶连续可导即f(n)(x)为连续函数，最多可导到n阶。

问：为什么一阶可导不能得出lim f’(x)存在？

答：如 (sin 1/x)’ = -1/x2 cos 1/x，当x=1/nΠ 和 x=1/nΠ+0.5Π时，不等，因此极限不存在。

【例题】2018

​ 一阶导数连续不能推出二阶导数存在、二阶可导可推出一阶连续可导

洛必达使用条件：https://mp.weixin.qq.com/s/E0KoLNOnxKoyTQz8NENJhA

[例题]（这里二阶能不能洛还是有点疑问，二阶连续可导不就可以洛吗？还是说这个结论错了，是至多洛到二，但存在不存在还是未知？）

单调性

​ f’(x0) > 0 可推出 f(x0) 单调增(只是一点)，f(x0)单调增不能推出 f’(x0) >0，如x3在x=0处f’(0) = 0，但x3是单调增的。

​ f’(0) > 0， 根据导数的定义式，只能得出在存在δ，使得在（0，δ）中 f(x) > f(0)，在（-δ，0）中f(x) < f(0)，而不能证明在x=0附近单调增。即只能说明0+附近的值比f(0)大【可能振荡】，而不能说明附近的单调性。反例如下 令 f ( x ) = { x + 2 x 2 sin ⁡ 1 x , x ≠ 0 0 , x = 0  则 x = 0 时 , f ′ ( 0 ) = lim ⁡ x → 0 x + 2 x 2 sin ⁡ 1 x x = 1 > 0 当 x ≠ 0 时 , f ′ ( x ) = 1 + 4 x  sin  1 x − 2 cos ⁡ 1 x f ′ ( 1 2 n π ) = − 1 < 0 \text {令} {f(x)}= \begin{cases}x+2x^{2} \sin \frac{1}{x}, & x \neq0\\0, & x=0\end{cases} \ 则\\ x=0 时, f^{\prime}(0)=\lim_{x \rightarrow0} \frac{x+2x^{2} \sin \frac{1}{x}}{x}=1>0 \\ 当x \neq0时, f^{\prime}(x)=1+4x{\text { sin } \frac{1}{x}-2\cos \frac{1}{x}} \\ f^{\prime}\left(\frac{1}{2n \pi}\right)=-1