命名实体识别主要方法

2024-06-02 10:49| 来源: 网络整理| 查看: 265

命名实体识别主要方法

命名实体识别（Named Entity Recognition，简称NER），又称作“专名识别”，是自然语言处理中的一项基础任务，应用范围非常广泛。命名实体一般指的是文本中具有特定意义或者指代性强的实体，通常包括人名、地名、机构名、日期时间、专有名词等。通常包括两部分：

实体的边界识别确定实体的类型（人名、地名、机构名或其他）

NER系统就是从非结构化的输入文本中抽取出上述实体，并且可以按照业务需求识别出更多类别的实体，比如产品名称、型号、价格等。因此实体这个概念可以很广，只要是业务需要的特殊文本片段都可以称为实体。

学术上NER所涉及的命名实体一般包括3大类（实体类，时间类，数字类）和7小类（人名、地名、组织机构名、时间、日期、货币、百分比）。

现状命名实体识别只是在有限的文本类型（主要是新闻语料中）和实体类别（主要是人名、地名）中取得了效果与其他信息检索领域相比，实体命名评测语料较小，容易产生过拟合命名实体识别更侧重高召回率，但在信息检索领域，高准确率更重要通用的识别多种类型的命名实体的系统性很差。中文难点汉语文本没有类似英文文本中空格之类的显式标示词的边界标示符，命名实体识别的第一步就是确定词的边界，即中文分词汉语分词和命名实体识别互相影响除了英语中定义的实体，外国人名译名和地名译名是存在于汉语中的两类特殊实体类型现代汉语文本，尤其是网络文本，常出现中英文交替使用，此时汉语命名实体识别的任务还包括识别其中的英文命名实体不同的命名实体具有不同的内部特征，不可能用一个统一的模型来刻画所有的实体内部特征现代汉语日新月异的发展给命名实体识别也带来了新的困难：（1）标注语料老旧，覆盖不全。譬如说，近年来起名字的习惯用字与以往相比有很大的变化，以及各种复姓识别、国外译名、网络红人、流行用语、虚拟人物和昵称的涌现。（2）命名实体歧义严重，消歧困难方法

在这里插入图片描述

基于规则和字典的方法

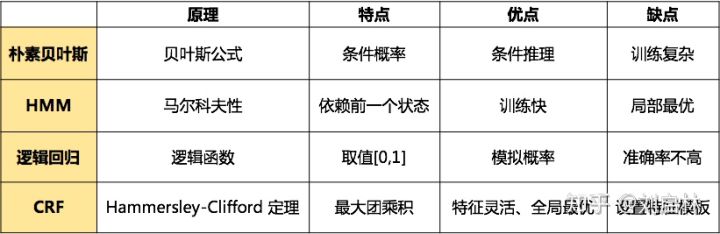
基于规则的方法多采用语言学专家手工构造规则模板，选用特征包括统计信息、标点符号、关键字、指示词和方向词、位置词(如尾字)、中心词等方法，以模式和字符串相匹配为主要手段，这类系统大多依赖于知识库和词典的建立。

基于规则和词典的方法是命名实体识别中最早使用的方法，它们依赖于手工规则的系统，都使用命名实体库，而且对每一个规则都赋予权值。当遇到规则冲突的时候，选择权值最高的规则来判别命名实体的类型。一般而言，当提取的规则能比较精确地反映语言现象时，基于规则的方法性能要优于基于统计的方法。但基于规则和字典的方法也有其缺陷：

规则往往依赖于具体语言、领域和文本风格，制定规则的过程耗时且难以涵盖所有的语言，特别容易产生错误，系统可移植性差，对于不同的系统需要语言学专家重新书写规则代价太大，存在系统建设周期长、需要建立不同领域知识库作为辅助以提高系统识别能力等问题基于统计学习的方法

基于统计机器学习的方法主要包括：**隐马尔可夫模型(Hidden Markov Moder, HMM)、最大熵模型(Maximum Entropy Model, MEM)、支持向量机(Support Vector Machine, SVM)、条件随机场(Conditional Random Field, crf)**等等。在基于机器学习的方法中，NER被当作序列标注问题。利用大规模语料来学习出标注模型，从而对句子的各个位置进行标注。NER 任务中的常用模型包括生成式模型HMM、判别式模型crf等。条件随机场（Conditional Random Field，crf）是NER目前的主流模型。

隐马尔可夫模型

隐马尔科夫模型（hidden Markov model，HMM），描述由一个隐藏的马尔科夫链随机生成不可观测的状态随机序列，再由各个状态（state）生成一个观测（observation）从而产生观测随机序列的过程。隐藏的马尔科夫链随机生成的状态的序列，称作状态序列（state sequence），它是模型的标签（target）；每个状态生成一个观测而产生的观测的随机序列，称为观测序列（observation sequence），它是模型的特征（features）。序列的每一个位置又可以看作是一个时刻。

马尔科夫链

有几种状态之间存在互相转换的概率

想推算出 x 1 → x 2 → x 3 x_1 \to x_2 \to x_3 x1→x2→x3的概率

这条链通常称为马尔可夫链

求解通常是利用 P ( x 1 ) P ( x 2 ∣ x 1 ) P ( x 3 ∣ x 1 , x 2 ) P(x_1)P(x_2|x_1)P(x_3|x_1,x_2) P(x1)P(x2∣x1)P(x3∣x1,x2)条件概率进行求解

隐马尔可夫模型

我们需要计算的东西不能直接获取其概率转化图

是根据另一种我们可见的观测东西去推算另一种东西

HMM五元组：观测序列-O （能获取的指标） M 个观测值 M个观测值 M个观测值状态序列-I （需要计算的指标） N N N个状态初始状态概率向量- π \pi π 初始时刻的概率 π 1 ∗ N \pi_{1*N} π1∗N状态转移概率矩阵- A A A 状态到状态的转移关系 A N ∗ N A_{N*N} AN∗N观测概率矩阵- B B B 状态转移到观测 B N ∗ M B_{N*M} BN∗M 两个基本假设：

齐次马尔可夫性假设：（状态只依赖于前一个时刻的状态） P ( i t ∣ i t − 1 , o t − 1 … , i 1 , o 1 ) = P ( i t ∣ i t − 1 ) , t = 1 , 2 , … , T P(i_t|i_{t-1},o_{t-1}\dots,i_1,o_1)=P(i_t|i_{t-1}),t=1,2,\dots,T \\ P(it∣it−1,ot−1…,i1,o1)=P(it∣it−1),t=1,2,…,T 观测独立性假设：(观测只依赖于当前时刻的状态) P ( o t ∣ i t , o t , i t − 1 , o t − 1 … i 1 , o 1 ) = P ( o t ∣ i t ) P(o_t|i_t,o_t,i_{t-1},o_{t-1}\dots i_1,o_1)=P(o_t|i_t) P(ot∣it,ot,it−1,ot−1…i1,o1)=P(ot∣it) 在这里插入图片描述

四面体、六面体、八面体🎲的例子

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Z0iMofqS-1648284595079)(HMM.png)]

HMM三类问题：概率计算问题

给定模型 λ = ( π , A , B ) \lambda=(\pi,A,B) λ=(π,A,B)和观测序列O的情况下，求 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)出现的概率（前向-后向算法）

前向概率计算

α t ( i ) = P ( o 1 , o 2 , … , o t , i t = q i ∣ λ ) = ∑ j = 1 N P ( i t − 1 = q j , i t = q i , o 1 t − 1 ) = ∑ j = 1 N P ( i t = q i , o t ∣ i t − 1 = q j , o 1 t − 1 ) ⋅ P ( i t − 1 = q j , o 1 t − 1 ) = ∑ j = 1 N P ( i t = q i , o t ∣ i t − 1 = q j ) ⋅ α t − 1 ( j ) = ∑ j = 1 N P ( o t ∣ i t = q i , i t − 1 = q j ) ⋅ P ( i t = q i ∣ i t − 1 = q j ) ⋅ α t − 1 ( j ) = ∑ j = 1 N b i ( o i ) ⋅ a j i ⋅ α t − 1 ( j ) \alpha_t(i)=P(o_1,o_2,\dots,o_t,i_t=q_i|\lambda) \\ =\sum\limits_{j=1}^NP(i_{t-1}=q_j,i_t=q_i,o_1^{t-1}) \\ =\sum\limits_{j=1}^NP(i_t=q_i,o_t|i_{t-1}=q_j,o_1^{t-1})\cdot P(i_{t-1}=q_j,o_1^{t-1}) \\ =\sum\limits_{j=1}^NP(i_t=q_i,o_t|i_{t-1}=q_j)\cdot \alpha_{t-1}(j)\\ =\sum\limits_{j=1}^NP(o_t|i_t=q_i,i_{t-1}=q_j) \cdot P(i_t=q_i|i_{t-1}=q_j) \cdot \alpha_{t-1}(j) \\ =\sum\limits_{j=1}^N b_i(o_i)\cdot a_{ji}\cdot \alpha_{t-1}(j) αt(i)=P(o1,o2,…,ot,it=qi∣λ)=j=1∑NP(it−1=qj,it=qi,o1t−1)=j=1∑NP(it=qi,ot∣it−1=qj,o1t−1)⋅P(it−1=qj,o1t−1)=j=1∑NP(it=qi,ot∣it−1=qj)⋅αt−1(j)=j=1∑NP(ot∣it=qi,it−1=qj)⋅P(it=qi∣it−1=qj)⋅αt−1(j)=j=1∑Nbi(oi)⋅aji⋅αt−1(j)

概率计算

P ( O ∣ λ ) = P ( o 1 T ∣ λ ) = ∑ i = 1 N P ( o 1 T , i T = q i ) = ∑ i = 1 N α T ( i ) P(O|\lambda) = P(o_1^T|\lambda) \\ =\sum\limits_{i=1}^NP(o_1^T,i_T=q_i) \\ =\sum\limits_{i=1}^N \alpha_T(i) P(O∣λ)=P(o1T∣λ)=i=1∑NP(o1T,iT=qi)=i=1∑NαT(i)

前向概率算法：

输入：隐马尔可夫模型 λ \lambda λ和观测序列 O O O

输出：观测序列概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)

初值 α t ( i ) = π i b i ( o 1 ) \alpha_t(i)=\pi_ib_i(o_1) αt(i)=πibi(o1) t = 1 , 2 , … , N t = 1,2,\dots,N t=1,2,…,N递推：对 t = 1 , 2 , … , T − 1 t=1,2,\dots,T-1 t=1,2,…,T−1 α t + 1 ( i ) = ∑ j = 1 N b i ( o i + 1 ⋅ a j i ⋅ α t ( j ) ) \alpha_{t+1}(i)=\sum\limits_{j=1}^Nb_i(o_{i+1} \cdot a_{ji} \cdot \alpha_t(j)) αt+1(i)=j=1∑Nbi(oi+1⋅aji⋅αt(j))终止： P ( O ∣ λ ) = ∑ j = 1 N α T ( i ) P(O|\lambda)=\sum\limits_{j=1}^N \alpha_T(i) P(O∣λ)=j=1∑NαT(i)

后向概率也是类似，从当前式子根据全概率公式展开，得到递推公式进行迭代

解码问题

给定模型 λ = ( π , A , B ) \lambda=(\pi,A,B) λ=(π,A,B)和观测序列O的情况下，求对给定观测序列条件概率 P ( I ∣ O ) P(I|O) P(I∣O)最大的状态序列I。即给定观测序列，求最有可能的对应状态序列（Viterbi算法）

定义两个矩阵

KaTeX parse error: Undefined control sequence: \var at position 1: \̲v̲a̲r̲是（序列长度，状态数量）形状的矩阵，每一行是一个时刻，每一列是由该状态输出的概率

KaTeX parse error: Undefined control sequence: \var at position 1: \̲v̲a̲r̲ ̲\ [0,0]表示时刻0，由状态0输出结果的概率

ϕ \phi ϕ里记录最有可能的路径

ϕ [ 1 , 0 ] \phi[1,0] ϕ[1,0]表示哪一个时刻0的状态最有可能转移到时刻1的状态0

学习问题

观测序列O已知的情况下，将状态序列作为隐数据I，求解 λ = ( π , A , B ) \lambda=(\pi,A,B) λ=(π,A,B)参数，使得在该模型下观测序列概率 P ( O ∣ λ ) P(O|\lambda) P(O∣λ)最大（极大似然估计算法）

方法

通过大量实验，能得出观测和状态序列。

逆推，通过第0位得出初始向量

统计次数之后，得出状态转移矩阵。

观测概率同理也可以求出来

最大熵模型

最大熵原理：首先满足已有的事实，在没有更多信息的情况下，那些不确定的部份都是“等可能的”

H ( p ) = − ∑ p ( x ) log ⁡ p ( x ) H(p)=-\sum p(x)\log p(x) H(p)=−∑p(x)logp(x)

max ⁡ p ( x ) H \max\limits_{p(x)}H p(x)maxH

0 ≤ H ( p ) ≤ log ⁡ ∣ X ∣ 0 \le H(p) \le \log|X| 0≤H(p)≤log∣X∣

EM算法

EM 算法，全称 Expectation Maximization Algorithm。期望最大算法是一种迭代算法，用于含有隐变量（Hidden Variable）的概率参数模型的最大似然估计或极大后验概率估计。

EM 算法的核心思想非常简单，分为两步：Expection-Step 和 Maximization-Step。E-Step 主要通过观察数据和现有模型来估计参数，然后用这个估计的参数值来计算似然函数的期望值；而 M-Step 是寻找似然函数最大化时对应的参数。由于算法会保证在每次迭代之后似然函数都会增加，所以函数最终会收敛。

核心思想是随机估计参数 θ \theta θ的值

用参数值和原始结果反过来计算新一轮的结果。

然后用极大似然反过来估计 θ A \theta_A θA和 θ B \theta_B θB。

直至参数收敛

不完全数据：观测随机变量Y —》 O

完全数据：观测随机变量 Y Y Y和隐随机变量 Z Z Z -------》 I

含有隐变量 Z Z Z的概率模型，目标是极大化观测变量Y关于参数 θ \theta θ的对数似然函数，即 max ⁡ θ L ( θ ) \max\limits_{\theta} L(\theta) θmaxL(θ) L ( θ ) = log ⁡ P ( Y ∣ θ ) = log ⁡ ∑ Z P ( Y , Z ∣ θ ) = log ⁡ ( ∑ Z P ( Y ∣ Z , θ ) P ( Z ∣ θ ) ) L(\theta)=\log P(Y|\theta) \\ =\log \sum\limits_Z P(Y,Z | \theta) \\ =\log(\sum\limits_Z P(Y|Z,\theta)P(Z|\theta)) L(θ)=logP(Y∣θ)=logZ∑P(Y,Z∣θ)=log(Z∑P(Y∣Z,θ)P(Z∣θ)) 对数似然函数 L ( θ ) L(\theta) L(θ)与第 i i i次迭代后的对数似然函数 L ( θ ( i ) ) L(\theta^{(i)}) L(θ(i))的差 L ( θ ) − L ( θ ( i ) ) = log ⁡ ( ∑ Z P ( Y ∣ Z , θ ) P ( Z ∣ θ ) ) − log ⁡ P ( Y ∣ θ ( i ) ) = log ⁡ ( ∑ Z P ( Z ∣ Y , θ ( i ) ) ) P ( Y ∣ Z , θ ) P ( Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) − log ⁡ P ( Y ∣ θ ( i ) ) ≥ ∑ Z P ( Z ∣ Y , θ ( i ) ) log ⁡ P ( Y ∣ Z , θ ) P ( Z ∣ θ ) P ( Z ∣ Y , θ ( i ) ) P ( Y ∣ θ ( i ) ) L(\theta)-L(\theta^{(i)})=\log (\sum\limits_{Z}P(Y|Z,\theta) P(Z|\theta) ) - \log P(Y|\theta^{(i)}) \\ = \log(\sum\limits_{Z}P(Z|Y,\theta^{(i)}))\frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})}-\log P(Y|\theta^{(i)}) \\ \ge \sum\limits_ZP(Z|Y,\theta^{(i)})\log \frac{P(Y|Z,\theta)P(Z|\theta)}{P(Z|Y,\theta^{(i)})P(Y|\theta^{(i)})} L(θ)−L(θ(i))=log(Z∑P(Y∣Z,θ)P(Z∣θ))−logP(Y∣θ(i))=log(Z∑P(Z∣Y,θ(i)))P(Z∣Y,θ(i))P(Y∣Z,θ)P(Z∣θ)−logP(Y∣θ(i))≥Z∑P(Z∣Y,θ(i))logP(Z∣Y,θ(i))P(Y∣θ(i))P(Y∣Z,θ)P(Z∣θ)

CRF

条件随机场

随机过程

设 T T T是一无限实数集，把依赖于参数 t ∈ T t \in T t∈T的一族（无限多个）随机变量称为随机过程，记为 { X ( t ) , t ∈ T } \{X(t),t \in T\} {X(t),t∈T}

随机场

若 T T T是 n n n维空间的某个子集，即 t t t是一个 n n n维向量，此时随机过程又称为条件随机场

相当于从平面映射到向量空间

马尔可夫随机场（概率无向图模型）

具有马尔可夫性的随机场

马尔可夫性：

P ( Y v ∣ X , Y w , w ≠ v ) = P ( Y v ∣ X , Y w , w − v ) P(Y_v|X,Y_w,w\ne v) = P(Y_v|X,Y_w,w-v) P(Yv∣X,Yw,w=v)=P(Yv∣X,Yw,w−v)

其中：

w − v w-v w−v表示在图 G ( V , E ) G(V,E) G(V,E)中与顶点v有边连接的所有顶点w

w ≠ v w\ne v w=v表示顶点 v v v以外的所有顶点

Y V Y_V YV与 Y W Y_W YW为顶点v与w的随机变量

团和最大团

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GMyGjqTr-1648284595081)(img/square.png)]

先考虑只有一条对角线的正方形，四个顶点为 Y 1 , Y 2 , Y 3 , Y 4 Y_1,Y_2,Y_3,Y_4 Y1,Y2,Y3,Y4。在 Y 2 , Y 3 Y_2,Y_3 Y2,Y3上连接了一条对角线

马尔可夫性： P ( Y 1 , Y 4 ∣ Y 3 , Y 2 ) = P ( Y 1 ∣ Y 2 , Y 3 ) × P ( Y 4 ∣ Y 2 , Y 3 ) P(Y_1,Y_4|Y_3,Y_2)=P(Y_1|Y_2,Y_3) \times P(Y_4|Y_2,Y_3) P(Y1,Y4∣Y3,Y2)=P(Y1∣Y2,Y3)×P(Y4∣Y2,Y3)

由马尔可夫性推导如下： P ( Y 1 , Y 2 , Y 3 ) ∗ P ( Y 2 , Y 3 , Y 4 ) / P ( Y 2 , Y 3 ) = P ( Y 1 , Y 2 , Y 3 , Y 4 ) P(Y_1,Y_2,Y_3) * P(Y_2,Y_3,Y_4) / P(Y_2,Y_3)=P(Y_1,Y_2,Y_3,Y_4) P(Y1,Y2,Y3)∗P(Y2,Y3,Y4)/P(Y2,Y3)=P(Y1,Y2,Y3,Y4)

此时，称 P ( Y 1 , Y 2 , Y 3 ) , P ( Y 2 , Y 3 , Y 4 ) P(Y_1,Y_2,Y_3) , P(Y_2,Y_3,Y_4) P(Y1,Y2,Y3),P(Y2,Y3,Y4)为最大团

团：两个节点在图中相邻

最大团：里面所有节点都是两两相连，并且不能扩展

P ( Y 2 , Y 3 ) = ∑ P ( Y 1 , Y 4 ∣ Y 2 , Y 3 ) = ∑ P ( Y 1 , Y 2 , Y 3 ) P ( Y 2 , Y 3 , Y 4 ) P(Y_2,Y_3)=\sum P(Y_1,Y_4|Y_2,Y_3)=\sum P(Y_1,Y_2,Y_3)P(Y_2,Y_3,Y_4) P(Y2,Y3)=∑P(Y1,Y4∣Y2,Y3)=∑P(Y1,Y2,Y3)P(Y2,Y3,Y4)

so P ( Y 1 , Y 2 , Y 3 , Y 4 ) = P ( Y 1 , Y 2 , Y 3 ) ∗ P ( Y 2 , Y 3 , Y 4 ) ∑ P ( Y 1 , Y 2 , Y 3 ) ∗ P ( Y 2 , Y 3 , Y 4 ) P(Y_1,Y_2,Y_3,Y_4)=\frac{P(Y_1,Y_2,Y_3)*P(Y_2,Y_3,Y_4)}{\sum P(Y_1,Y_2,Y_3)*P(Y_2,Y_3,Y_4)} P(Y1,Y2,Y3,Y4)=∑P(Y1,Y2,Y3)∗P(Y2,Y3,Y4)P(Y1,Y2,Y3)∗P(Y2,Y3,Y4)

令最大团的概率为 ϕ 1 , ϕ 2 \phi_1,\phi_2 ϕ1,ϕ2

P ( Y 1 , Y 2 , Y 3 , Y 4 ) = ϕ 1 ϕ 2 ∑ ϕ 1 ϕ 2 P(Y_1,Y_2,Y_3,Y_4)=\frac{\phi_1\phi_2}{\sum \phi_1\phi_2} P(Y1,Y2,Y3,Y4)=∑ϕ1ϕ2ϕ1ϕ2

可以推导到无限维的情况下

概率无向图模型的因子分解

给定概率无向图模型，设其无向图为G，C为G上的最大团， Y C Y_C YC表示C对应的随机变量，那么概率无向图模型的联合概率分布 P ( Y ) P(Y) P(Y)可写作图中所有最大团C上的函数 φ C ( Y C ) \varphi_C(Y_C) φC(YC)的乘积形式

P ( Y ) = 1 Z ∏ C φ C ( Y C ) P(Y)=\frac{1}{Z}\prod\limits_C\varphi_C(Y_C) P(Y)=Z1C∏φC(YC)

Z = ∑ ∑ C φ C ( Y C ) Z=\sum \sum\limits_C \varphi_C(Y_C) Z=∑C∑φC(YC)

条件随机场定义

设 X X X与 Y Y Y是随机变量， P ( Y ∣ X ) P(Y|X) P(Y∣X)是在给定 X X X的条件 Y Y Y的条件概率分布

若随机变量 Y Y Y构成一个由无向图 G = ( V , E ) G=(V,E) G=(V,E)表示的马尔可夫随机场，即

P ( Y V ∣ X , Y W , w ≠ v ) = P ( Y V ∣ X , Y W , w − v ) P(Y_V|X,Y_W,w\ne v)=P(Y_V|X,Y_W,w-v) P(YV∣X,YW,w=v)=P(YV∣X,YW,w−v)对任意顶点 v v v成立，则称条件概率分布 P ( Y ∣ X ) P(Y|X) P(Y∣X)为条件随机场

对应到线性链的条件随机场 HMM模型（最大团为两个顶点的集合）

在这里插入图片描述

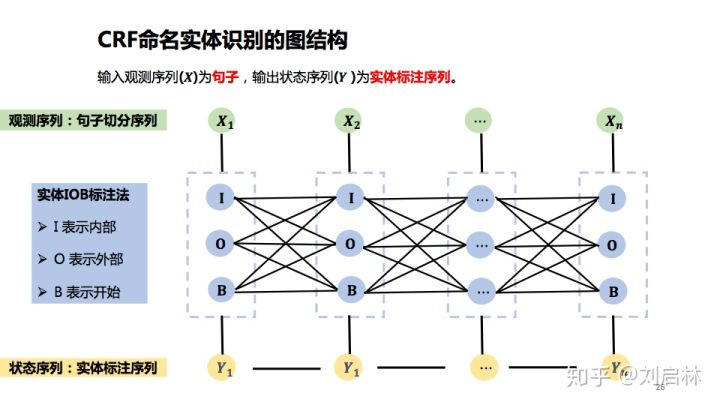
在命名实体识别中，观测序列为句子中的一个个单词，状态序列为词性

最大团为三角形

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Pv00HWLE-1648284595082)(img/link.png)]

线性链条件随机场公式

设 P ( y ∣ x ) = 1 Z ( x ) e x p ( ∑ i , k λ k t k ( y i − 1 , y i , x , i ) + ∑ i , l u l s l ( y i , x , i ) ) P(y|x)=\frac{1}{Z(x)}exp(\sum\limits_{i,k}\lambda_kt_k(y_{i-1,y_i,x,i})+\sum\limits_{i,l}u_ls_l(y_i,x,i)) P(y∣x)=Z(x)1exp(i,k∑λktk(yi−1,yi,x,i)+i,l∑ulsl(yi,x,i))

其中： Z ( x ) = ∑ y e x p ( ∑ i , k λ k t k ( y i − 1 , y i , x , i ) + ∑ i , l u l s l ( y i , x , i ) ) Z(x)=\sum\limits_yexp(\sum\limits_{i,k}\lambda_kt_k(y_{i-1},y_i,x,i)+\sum\limits_{i,l}u_ls_l(y_i,x,i)) Z(x)=y∑exp(i,k∑λktk(yi−1,yi,x,i)+i,l∑ulsl(yi,x,i))

t k , s l t_k,s_l tk,sl：特征函数

λ k , u l \lambda_k,u_l λk,ul：对应权值

Z ( x ) Z(x) Z(x)：归一化因子

CRF应用中文分词

观测序列：句子

状态序列：词位序列

BMES：（B词首，M词中，E词尾，S独立词）

命名实体识别词的实体标注

首先把句子进行原子切分，然后对字（词）进行实体标注

确定特征函数

接着，确定特征模板。一般采用当前位置的前后n个位置上的词

f ( y w 0 s n x w 0 s n ) = 1 o r 0 f(y_{w_0sn}x_{w_0sn})=1 \ or \ 0 f(yw0snxw0sn)=1 or 0

模型训练

训练CRFF模型参数

P ( y ∣ x ) = 1 Z ( x ) e x p ∑ k = 1 K w k f k ( f , x ) P(y|x)=\frac{1}{Z(x)}exp\sum\limits_{k=1}^Kw_kf_k(f,x) P(y∣x)=Z(x)1expk=1∑Kwkfk(f,x)