|
1,矩阵序列
1.1,矩阵序列
设  中的矩阵序列 中的矩阵序列  ,其中 ,其中  。若: 。若:

则称矩阵序列 收敛于 收敛于  ,或称 ,或称  为矩阵序列 为矩阵序列 的极限,记为: 的极限,记为:
 或 或 
(1)不收敛的矩阵序列称为发散。
(2)矩阵序列收敛的本质是矩阵的所有元素都收敛。
(3) 上一个矩阵序列的收敛相当于 上一个矩阵序列的收敛相当于  个数列同时收敛。 个数列同时收敛。
(4)用初等分析法太繁琐。
(5)与向量序列一样,可以利用矩阵范数来研究矩阵序列的收敛问题。
设  ,则: ,则:

其中  是 是 上的任一矩阵范数。 上的任一矩阵范数。
证明:

当矩阵序列收敛时,矩阵序列的任意范数也收敛,反之不成立。
设  ,则: ,则:

其中  是 是  上的任一矩阵范数。 上的任一矩阵范数。
收敛的矩阵序列的性质:
设  为适当阶的矩阵, 为适当阶的矩阵, ,则: ,则:
(1)
(2)
(3)当  和 和  均可逆时, 均可逆时,
证明: 可逆不能保证 可逆不能保证 可逆 可逆

对每一个  都有可逆矩阵 都有可逆矩阵  ,但 ,但  不可逆。 不可逆。
1.2,幂收敛矩阵
设  ,若 ,若  ,则称 ,则称  为收敛矩阵。 为收敛矩阵。
设 ,则 ,则  是收敛矩阵的充要条件是 是收敛矩阵的充要条件是  。 。
设  ,若对 ,若对  上的某个矩阵范数 上的某个矩阵范数  有 有  ,则 ,则  为收敛矩阵。 为收敛矩阵。
借助矩阵的谱半径或矩阵的范数来判断矩阵是否收敛。
【例1】判断下列矩阵是否为收敛矩阵

可求得  ,故 ,故  是收敛矩阵。 是收敛矩阵。

因为  ,故 ,故  是收敛矩阵。 是收敛矩阵。
2,矩阵级数
2.1,矩阵级数
由  中的矩阵序列 中的矩阵序列  构成的无穷和: 构成的无穷和:

称为矩阵级数,记为  ,对任一正整数 ,对任一正整数  ,称为矩阵级数,记为 ,称为矩阵级数,记为  。 。
对任一正整数  ,称 ,称  为矩阵级数的部分和,如果由部分和构成的矩阵序列 为矩阵级数的部分和,如果由部分和构成的矩阵序列  收敛,且有极限 收敛,且有极限  ,即 ,即  ,则称矩阵级数 ,则称矩阵级数  收敛, 收敛,
且有和  ,记为 ,记为  不收敛的矩阵级数称为发散的。 不收敛的矩阵级数称为发散的。
如果记由  ,显然 ,显然  相当于 相当于
 ,即 ,即  个数项级数都收敛。 个数项级数都收敛。
【例1】已知  ,研究矩阵级数 ,研究矩阵级数  的敛散性。 的敛散性。
因为 
所以 
故所给矩阵级数收敛,且和为  。 。
设  ,如果 ,如果  个数项级数 个数项级数  都绝对收敛,即 都绝对收敛,即  都收敛,则称矩阵级数 都收敛,则称矩阵级数  绝对收敛。 绝对收敛。
利用矩阵范数,可以将判定矩阵级数的绝对收敛问题转化为判定正项级数是否收敛的问题。
设  ,则矩阵级数 ,则矩阵级数  绝对收敛的充分必要条件是正项级数 绝对收敛的充分必要条件是正项级数  绝对收敛的充分必要条件是正项级数 绝对收敛的充分必要条件是正项级数  收敛,其中 收敛,其中  是 是  上任一矩阵范数。 上任一矩阵范数。
矩阵级数性质:设  ,其中 ,其中  是适当阶的矩阵,则: 是适当阶的矩阵,则:
(1)
(2)绝对收敛的矩阵级数必收敛,并且任一调换其项的顺序所得的矩阵级数仍收敛,且其和不变。
(3)若矩阵级数  收敛(或绝对收敛),则矩阵级数 收敛(或绝对收敛),则矩阵级数  也收敛(或绝对收敛),并且有: 也收敛(或绝对收敛),并且有: 。 。
(4)若  和 和  均绝对收敛,则它们的项数相乘所得的矩阵级数: 均绝对收敛,则它们的项数相乘所得的矩阵级数:

也绝对首先,且其和为  。 。
2.2,矩阵幂级数
设  , , ,称矩阵级数 ,称矩阵级数  为矩阵 为矩阵  的幂级数。 的幂级数。
(1)利用定义判断矩阵幂级数的收敛性很不方便。
(2)矩阵幂级数是复变量 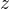 的幂级数 的幂级数  的推广。如果幂级数 的推广。如果幂级数 的收敛半径为 的收敛半径为  ,则对收敛圆 ,则对收敛圆  内的所有 内的所有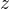 , ,  都是绝对收敛的。因此,讨论 都是绝对收敛的。因此,讨论  的敛散性问题可以自然的联系到 的敛散性问题可以自然的联系到  的收敛半径。 的收敛半径。
设幂级数  的收敛半径为 的收敛半径为  , , ,则: ,则:
(1)当  时,矩阵幂级数 时,矩阵幂级数  绝对收敛。 绝对收敛。
(2)当  时,矩阵幂级数 时,矩阵幂级数  发散。 发散。
推论:设幂级数  的收敛半径是 的收敛半径是  , , ,若存在 ,若存在  上的某个矩阵范数 上的某个矩阵范数  使得 使得  ,则矩阵幂级数 ,则矩阵幂级数  绝对收敛。 绝对收敛。
【例2】判断矩阵幂级数  的敛散性。 的敛散性。
令  ,可求得 ,可求得  ,由于幂级数收敛半径 ,由于幂级数收敛半径  ,所以 ,所以  收敛。 收敛。
收敛半径:
2.3,Neumann级数
设  ,矩阵幂级数 ,矩阵幂级数  (称为Neumann级数)收敛 (称为Neumann级数)收敛   ,并且在收敛时其和为 ,并且在收敛时其和为  。 。
【例3】已知  ,判定矩阵幂级数 ,判定矩阵幂级数  的收敛性,试求其和。 的收敛性,试求其和。
因为  ,所以 ,所以  收敛,且 收敛,且

3,矩阵函数
3.1,矩阵函数的概念
设幂级数  的收敛半径为 的收敛半径为  ,且当 ,且当  时,幂级数收敛于函数 时,幂级数收敛于函数  ,即: ,即:

如果  满足 满足  ,则称收敛的矩阵幂级数 ,则称收敛的矩阵幂级数  的和为矩阵函数,记为: 的和为矩阵函数,记为: ,即 ,即

常见矩阵函数:
   
如果把矩阵函数  的变元 的变元  换成 换成  其中 其中  为参数,则相应得到: 为参数,则相应得到:

3.2,矩阵函数的计算
方法一:利用Hamilton-Cayley定理:利用Hamilton-Cayley定理找出矩阵方幂之间的关系,然后化简矩阵幂级数,求出矩阵函数的值。
【例4】已知  ,求 ,求  。 。
 ,由Hamilton-Cayley定理知 ,由Hamilton-Cayley定理知 



【例5】已知  阶矩阵 阶矩阵  的特征值为 的特征值为  ,求 ,求 
由于  ,因此 ,因此 
进而 






方法而:利用相似对角化:已知  是可对角化的,计算函数 是可对角化的,计算函数  ,由于 ,由于  可对角化,即存在 可对角化,即存在  ,使得 ,使得

则有:



同理可证:
【例6】已知  ,求 ,求  , , 。 。
通过计算特征多项式和特征向量可得:
 , ,
故 

方法三:利用Jordan标准形:设  ,则存在 ,则存在  ,使得 ,使得

其中  是特征值 是特征值  对应的Jordan块。 对应的Jordan块。



设  , , 是 是  的 的  个特征值,则矩阵函数 个特征值,则矩阵函数  的特征值为: 的特征值为:

【例7】已知  ,求 ,求  。 。
通过计算特征多项式和特征向量可得:

故 

方法四:待定系数法:用待定系数法求矩阵函数  或 或  的步骤如下: 的步骤如下:
(1)求矩阵  的特征多项式。 的特征多项式。
(2)设  ,根据 ,根据  或 或  , , ,列方程组求解 ,列方程组求解  。 。
(3)计算  或 或  = =
【例8】已知  ,求 ,求  。 。
可求得  ,设 ,设 
则由 

同理 

如果求得次数比矩阵  特征多项式低的零化多项式——最小多项式 特征多项式低的零化多项式——最小多项式
则计算矩阵函数就更容易一些。
【例9】已知  ,求 ,求  。 。
可求得  的Jordan标准形为 的Jordan标准形为 
于是  的最小多项式为 的最小多项式为 
设 
由 
于是 
又由于 
故 
3.3,矩阵函数的性质
常见的矩阵函数有  ,它们有些性质与普通的指数函数和三角函数相同;有些性质与一般指数函数和三角函数不同,这是由于矩阵乘法不满足交换律。 ,它们有些性质与普通的指数函数和三角函数相同;有些性质与一般指数函数和三角函数不同,这是由于矩阵乘法不满足交换律。
对任意  ,总有: ,总有:
(1) , ,
(2) , , , ,
对任意  ,且 ,且  ,则: ,则:
(1)
(2)
(3)
对任意  ,则有: ,则有:
(1)
4,矩阵的微分和积分
4.1,函数矩阵的微分和积分
设以变量  的函数为元素的矩阵 的函数为元素的矩阵  称为函数矩阵,其中 称为函数矩阵,其中  都是变量 都是变量  的函数。 的函数。
(1)若 ![\small t\in[a,b]](https://latex.csdn.net/eq?%5Cdpi%7B120%7D%20%5Csmall%20t%5Cin%5Ba%2Cb%5D) ,则称 ,则称  是定义在 是定义在 ![\small [a,b]](https://latex.csdn.net/eq?%5Cdpi%7B120%7D%20%5Csmall%20%5Ba%2Cb%5D) 上的。 上的。
(2)又若每个  在 在 ![\small [a,b]](https://latex.csdn.net/eq?%5Cdpi%7B120%7D%20%5Csmall%20%5Ba%2Cb%5D) 上连续、可微、可积,则称 上连续、可微、可积,则称 在 在![\small [a,b]](https://latex.csdn.net/eq?%5Cdpi%7B120%7D%20%5Csmall%20%5Ba%2Cb%5D) 上连续、可微、可积的。 上连续、可微、可积的。
(3)当 可微时,规定其导数为: 可微时,规定其导数为:
(4)当 在 在![\small [a,b]](https://latex.csdn.net/eq?%5Cdpi%7B120%7D%20%5Csmall%20%5Ba%2Cb%5D) 上可积时,规定 上可积时,规定 在 在![\small [a,b]](https://latex.csdn.net/eq?%5Cdpi%7B120%7D%20%5Csmall%20%5Ba%2Cb%5D) 上积分为: 上积分为:
【例10】求函数矩阵  的导数 的导数

设  与 与  为适当阶的可微矩阵,则: 为适当阶的可微矩阵,则:
(1)
(2)当  是可微函数时,有 是可微函数时,有 
(3)
(4)当  关于 关于  可微时,有 可微时,有 
(5)当  是可微矩阵时,有 是可微矩阵时,有 
(6)由于  仍是函数矩阵,如果它仍是可导的,即可以定义其二阶导数。 仍是函数矩阵,如果它仍是可导的,即可以定义其二阶导数。
(7)函数矩阵的高阶导数:
设  ,则有(利用逐项求导的方法) ,则有(利用逐项求导的方法)
(1)
(2)
(3) 
设  与 与  是区间 是区间 ![\small [a,b]](https://latex.csdn.net/eq?%5Cdpi%7B120%7D%20%5Csmall%20%5Ba%2Cb%5D) 上适当阶的可积矩阵, 上适当阶的可积矩阵, 是适当阶的常数矩阵, 是适当阶的常数矩阵, ,则: ,则:
(1)
(2)
(3) , ,
(4)若  在区间 在区间![\small [a,b]](https://latex.csdn.net/eq?%5Cdpi%7B120%7D%20%5Csmall%20%5Ba%2Cb%5D) 上连续,则对任意 上连续,则对任意  ,有 ,有 
(5)若  在区间 在区间![\small [a,b]](https://latex.csdn.net/eq?%5Cdpi%7B120%7D%20%5Csmall%20%5Ba%2Cb%5D) 上连续可微时,有 上连续可微时,有 
4.2,数量矩阵对矩阵变量的导数
设  是以矩阵 是以矩阵  为自变量的 为自变量的  元函数,且 元函数,且  都存在,规定 都存在,规定  对矩阵变量 对矩阵变量  的导数为 的导数为  为: 为:

特别的,以  为自变量的函数 为自变量的函数  的导数: 的导数:
![\small \frac{df}{dx}=\left [ \frac{df}{d\xi _1},\frac{df}{d\xi _2},...,\frac{df}{d\xi _n} \right ]^T](https://latex.csdn.net/eq?%5Cdpi%7B120%7D%20%5Csmall%20%5Cfrac%7Bdf%7D%7Bdx%7D%3D%5Cleft%20%5B%20%5Cfrac%7Bdf%7D%7Bd%5Cxi%20_1%7D%2C%5Cfrac%7Bdf%7D%7Bd%5Cxi%20_2%7D%2C...%2C%5Cfrac%7Bdf%7D%7Bd%5Cxi%20_n%7D%20%5Cright%20%5D%5ET)
称为数量函数对向量变量的导数,记为  。 。
设  是给定的向量, 是给定的向量, 为向量变量,且 为向量变量,且  ,求 ,求  。 。
解:因为  , ,
所以 ![\small \frac{df}{dx}=\left [\frac{\partial f}{\partial \xi_1} ,\frac{\partial f}{\partial \xi_2} ,...,\frac{\partial f}{\partial \xi_n} \right ]^T=\left ( a_1,a_2,...,a_n \right )^T=\alpha](https://latex.csdn.net/eq?%5Cdpi%7B120%7D%20%5Csmall%20%5Cfrac%7Bdf%7D%7Bdx%7D%3D%5Cleft%20%5B%5Cfrac%7B%5Cpartial%20f%7D%7B%5Cpartial%20%5Cxi_1%7D%20%2C%5Cfrac%7B%5Cpartial%20f%7D%7B%5Cpartial%20%5Cxi_2%7D%20%2C...%2C%5Cfrac%7B%5Cpartial%20f%7D%7B%5Cpartial%20%5Cxi_n%7D%20%5Cright%20%5D%5ET%3D%5Cleft%20%28%20a_1%2Ca_2%2C...%2Ca_n%20%5Cright%20%29%5ET%3D%5Calpha)
设  是给定的矩阵, 是给定的矩阵, 是矩阵变量,且 是矩阵变量,且  ,求 ,求  。 。
解:因为 
所以 
而 
故 
设  是给定的矩阵, 是给定的矩阵, 是向量变量,且 是向量变量,且  ,求 ,求  。 。
解:因为 
所以 
所以 
4.3,矩阵值函数对矩阵变量的导数
设矩阵  的元素 的元素  都是以矩阵变量 都是以矩阵变量  的函数,称 的函数,称  为矩阵值函数,规定 为矩阵值函数,规定  对矩阵变量 对矩阵变量  的导数为 的导数为  。 。
 ,其中 ,其中 
其结果为  的矩阵。 的矩阵。
设  为向量变量,求 为向量变量,求  和 和  。 。
由定义得,
类似由定义得,
5,矩阵分析应用举例
5.1,一阶常系数线性微分方程组
有常系数微分方程组

满足初始条件  的解。 的解。
 , , , , , ,
则上述微分方程组可写为:

通过常数变异法来求解
因为 
在 ![\small [t_0,t]](https://latex.csdn.net/eq?%5Cdpi%7B120%7D%20%5Csmall%20%5Bt_0%2Ct%5D) 上积分,得 上积分,得

于是微粉刺方程组的解为:
【例11】求解微分方程组初值问题。

记  , , , , , ,
则微分方程组能写成矩阵的形式:

可求得:
因此微分方程的解为:
 , ,

故微分方程组的解为:
5.2,Lyapunov矩阵方程AX+BX=F
在控制论和系统理论中,会遇到形如: 的矩阵方程,这个方程也称为 Lyapunov方程,关于这个方程的解有如下结果: 的矩阵方程,这个方程也称为 Lyapunov方程,关于这个方程的解有如下结果:
给定矩阵方程:

其中  ,如果 ,如果  和 和  的所有特征值都具有负实部,则该方程组有唯一解: 的所有特征值都具有负实部,则该方程组有唯一解:
设  ,则微分方程: ,则微分方程:

的解为:
设  ,且 ,且  的所有特征值具有负实部,则矩阵方程: 的所有特征值具有负实部,则矩阵方程:

的唯一解为:
如果  是 是  正定矩阵,则 正定矩阵,则 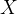 也是 也是 正定矩阵。 正定矩阵。
5.3,最小二乘问题
在矩阵论实际应用中,最小二乘法是一种很重要的方法。因为实验有误差,数据有偏差,如何在纷乱复杂的环境中找到最优选择,最小二乘法就是解决该问题的一种重要方法。
【例12】现有 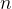 组数据: 组数据: ,试将它们拟合为一条直线。 ,试将它们拟合为一条直线。
设这条直线为: ,由于各种实际原因使: ,由于各种实际原因使:

则可构造误差

为了不使得误差正负抵消,造成小的假象,进一步采取  平方和作为目标函数,即: 平方和作为目标函数,即:
![\varepsilon =\sum_{i=1}^n\varepsilon _i^2=\sum_{i=1}^n[y_i-(kx_i+b)]^2](https://latex.csdn.net/eq?%5Cvarepsilon%20%3D%5Csum_%7Bi%3D1%7D%5En%5Cvarepsilon%20_i%5E2%3D%5Csum_%7Bi%3D1%7D%5En%5By_i-%28kx_i+b%29%5D%5E2)
希望求出最佳逼近对应的 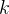 和 和 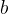 使得目标函数为 使得目标函数为  ,也即最小二乘解。 ,也即最小二乘解。
令 
也就是 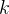 和 和 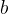 的二元一次方程: 的二元一次方程:

令 
最小二乘解为 
设  ,当线性方程组 ,当线性方程组 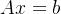 无解时,则对任意 无解时,则对任意  都有 都有  。 。
此时希望找到这样的向量  ,它使得 ,它使得  取到 取到  的最小值。 的最小值。
即: 。 。
称这个问题为最小二乘问题,称 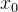 为矛盾方程组 为矛盾方程组 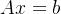 的最小二乘解。 的最小二乘解。
设  ,若 ,若  是 是 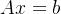 的最小二乘解,则 的最小二乘解,则 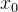 是方程组 是方程组

的解,称上式为 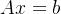 的法方程组。 的法方程组。
证明:由于

若 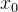 为 为 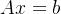 的最小二乘解,则它应是 的最小二乘解,则它应是 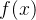 极小值点,从而 极小值点,从而

推论1:若 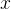 和 和 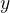 都是矛盾方程 都是矛盾方程 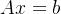 最小二乘解,则 最小二乘解,则  或 或  。 。
推论2:若 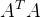 非奇异,则矛盾方程 非奇异,则矛盾方程 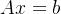 的最小二乘解为: 的最小二乘解为: ,且解唯一。 ,且解唯一。
【例13】设  ,且 ,且  有解。 有解。
试求约束最小化问题: 的解满足的代数方程, 的解满足的代数方程,
也就是求 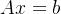 在约束条件 在约束条件  的最小二乘解所满足的代数方程。 的最小二乘解所满足的代数方程。
若  为 为  的极值点,则应有: 的极值点,则应有:

这说明极值点  应满足方程: 应满足方程:

求解该方程组即可得到 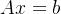 在约束条件 在约束条件  下的最小二乘解 下的最小二乘解 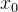 。 。
|