相似度系数Corr的解释与Matlab代码实现

相关系数：考察两个事物（在数据里我们称之为变量）之间的相关程度

如果有两个变量：X、Y，最终计算出的相关系数的含义可以有如下理解：

（1）当相关系数为0时，X和Y两变量无关系。

（2）当X的值增大（减小），Y值增大（减小），两个变量为正相关，相关系数在0.00与1.00之间

（3）当X的值增大（减小），Y值减小（增大），两个变量为负相关，相关系数在-1.00与0.00之间

（4）相关系数的绝对值越大，相关性越强，相关系数越接近于1或-1，相关度越强；相关系数越接近于0，相关度越弱

通常情况下通过以下取值范围判断变量的相关强度

相关系数 0.8-1.0 极强相关

0.6-0.8 强相关

0.4-0.6 中等强度相关

0.2-0.4 弱相关

0.0-0.2 极弱相关或无相关

有关相关系数的数学意义与Matlab编程解释，有兴趣的话可以关注下以下视频教程

1. 二维相关系数

R=corr2(A,B) %返回数组A和B之间的二维相关系数

corr2使用以下公式计算相关系数

①mean();

mean函数的主要作用是求列或行的平均数

对列求平均数

mean(A,1)=mean(A)

对行求平均值

mean(A,2)

②mean2();

相当于mean(mean(A)),相当于对整一个矩阵求像素平均值

例如：计算图像和用中位数滤波器进行了处理的同一图像之间的相关系数

I=imread(‘lina.jpg’);

J=medfilt2(I);

R=corr2(I,J)

R=0.9959

2. Pearson相关系数

皮尔逊相关也称为积差相关（或积矩相关），度量两个变量之间的线性关系程度，相关系数可以是介于-1和+1之间的值。如果一个变量在另一个变量下降时倾向于上升，则相关系数为负数。相反，如果两个变量倾向于同时上升，则相关系数为正数。

假设有两个变量X、Y，那么两变量间的皮尔逊相关系数可通过以下公式计算：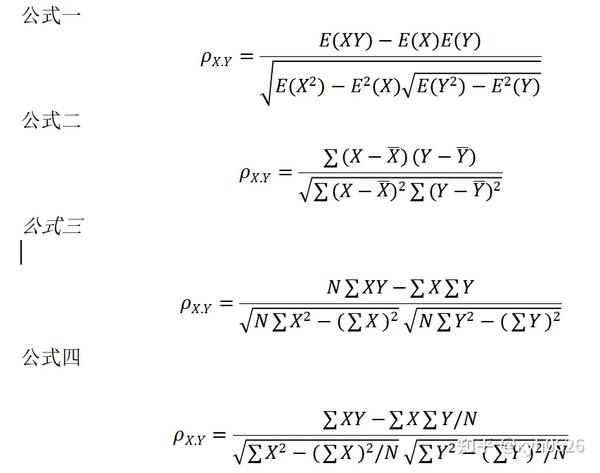

以上列出的四个公式等价，其中E是数学期望，cov表示协方差，N表示变量取值的个数。

当两个变量的标准差都不为零时，相关系数才有定义，皮尔逊相关系数适用于：

（1）两个变量之间是线性关系，都是连续数据。

（2）两个变量的总体是正态分布，或接近正态的单峰分布。

（3）两个变量的观测值是成对的，每对观测值之间相互对立。

Matlab实现

皮尔逊相关系数的Matlab实现（依据公式四实现）

function coeff=myPearson(X,Y)

%本函数实现了皮尔逊相关系数的计算操作

%

%输入：

%X：输入的数值序列

%Y：输入的数值数列

%

%输出

%coeff:两个输入数值序列X，Y的相关系数

%

if length(X)~=length(Y)

error(‘两个数值序列的维数不相等’)；

return;

end

fenzi=sum(X.*Y)-(sum(X)*sum(Y))/length(X);

fenmu=sqrt(sum(X.^2)-sum(X)^2/length(X)*(sum(Y.^2)-sum(Y)^2/length(X)));

coeff=fenzi/fenmu;

end%函数myPearson结束

或者也可以用Matlab中内置Pearson函数实现：

x=[1;2;3];

y=[2;5;6];

r1=corr(x,y,’type’,’Pearson’); %相关系数

r2=corrcoef(x,y); % R=corrcoef（X）returns a matrix R of correlation coefficients calculated from an input matrix X whose rows are observations and whose columns are variables. The matrix R=corrcoef(X) is related to the covariance matrix C=cov(X) by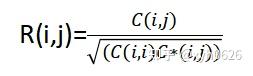

corrcoef(X) is the zeroth lag of the normalized covariance function, that is, the zeroth lag of xcov(x,’coeff’) packed into a square array.

协方差 cov(x)

—x为一个样本容量

—x为一个样本矩阵

首先看看均值，样本方差，样本协方差公式区别

3. Spearman相关系数

斯皮尔曼相关系数被定义成等级之间的皮尔逊相关系数。

斯皮尔曼相关系数（Spearman）也被叫作斯皮尔曼等级相关系数，同样用于衡量两个变量之间的相关性，在之前对皮尔逊相关系数的介绍中，我们提到了在进行皮尔逊相关系数运算的时候需要确定数据是否复合正态分布等等。有人移除了另一种方法，即用数据的大小来代替数据本身。

这种替代方法，本身也是一种消除量纲的过程，我们提到了从协方差到皮尔逊相关的过程中，需要消除量纲，同样的从另一个角度出发，斯皮尔曼相关系数使用排序的方法消除量纲，在相关性分析中，用数据大小的排序代替原始的数据，也起到了消除量纲的作用，同时在分级数据比如优、良、中的等级数据中，我们适合使用斯皮尔曼相关系数。

连续数据，满足正态分布，判断是否具有线性相关性的时候用皮尔逊相关系数较为合适，如果不满足条件的话，我们应该私用斯皮尔曼相关系数。

①斯皮尔曼相关系数计算

我们举一个身高和睡眠时间的例子来说明斯皮尔曼相关系数的计算方法，第一步我们需要将数据从小打到大的顺序并给出所属的等级，当两个数据的等值相等的时候，我们计算数值等级的平均值作为等级数，比如身高栏中，身高栏的160有两个，应该排第三名和第四名，平均下来的等级应该是3.5.同理，我们也将睡眠时间的等级进行排序，得到等级大小排序。之后我们计算两组数据的等级差记为d用于计算斯皮尔曼相关系数。

斯皮尔曼相关系数的具体计算方法如下：

其中n是样本容量，di代表数据x和y之间的等级差(一个数的等级，就是将它所在的一列数按照从小到大排序后，这个数所在的位置)。在Matlab中，为了计算斯皮尔曼相关系数我们可以直接使用corr指令。具体形式如下：

corr(x,y,’type’,’Spearman’)

②斯皮尔曼相关系数检验

和皮尔逊相关系数一样，在斯皮尔曼相关系数的计算中，得到了数值我们也无法知晓到底相关系数多大才是相关性强，多小才是相关性弱，为了表明强弱关系，我们需要引入假设检验的方法。

小样本假设检验

斯皮尔曼相关系数的假设检验分为两类，一个是小样本的情况，即样本的数量小于30的情况下时，可以直接使用查表的方式进行验证。虽然在不是那么严格的情况下，我们的样本数量大于30的时候也可以参考表格。

当我们的相关系数大于等于表中的临界值的时候，我们认为相关系数是有显著差异的，即有相关性，相关性不为0.

2.2大样本假设检验

在大样本的情况下，我们可以通过构建统计量的方式进行假设检验，大牛们总结了在以下的统计量是符合正态分布的。因此，当样本数量大于30的时候，我们可以用如下的方法构建统计量，计算p值

在matlab中，如果是双侧检验的话我们的p值计算方式如下

p=(1-normcdf(x))*2;

其中x就是我们构建的统计量，r乘样本数减1开根号。在得到的p值中，如果p值大于0.05，则没有显著性差异，也就是说名没有理由认为显著性差异存在，即没有相关性。如果p值小于0.05的话，我们可以认为存在显著性差异。

③结论

斯皮尔曼相关系数，也叫做斯皮尔曼等级相关系数，就是因为它通过等级排序的方式将数值转化为了等级排序，可以方便的应用在非正态性的数据，或者是评级的数据中，用于相关性的检验。如果说数据满足正态分布，而且连续，那么还是建议用散点图，加上皮尔逊相关系数以及假设检验的方式判断数据之间的相关性。

两种方法对比

（1）corr(X,Y,’type’,’Spearman’);

这里的X和Y必须是列向量

（2）corr(X,’type’,’Sphereman’)

这是计算X矩阵各列之间的斯皮尔曼相关系数

斯皮尔曼相关系数的适用条件比皮尔逊相关系数要广，只要数据满足单调关系

（例如线性函数、指数函数、对数函数等）就能够使用。

附：

一、基本统计量：

均值mean(x) 中位数median(x) 标准差std(x)

方差var(x) 偏度skewness(x) 峰度kurtosis(x)

常见的概率分布函数

正态分布：norm 指数分布 exp 泊松分布 poiss

beta分布：beta 威布尔分布：weib kafang分布：chi2

t分布：t f分布：F

工具箱对每一种分布都提供五类函数，其命令字符为：

概率密度：pdf

概率分布：cdf

逆概率分布：inv

均值与方差：stat

随机数生成：rnd

参数估计：fit

当需要一种分布的某一类函数时，将以上所列的分布命令字符与函数命令接起来并输入自变量（可以是标量、数组或矩阵）结合参数即可。

对均值为mu,标准差为sigma的正态分布，举例：

1. 概率密度函数

p=normpdf(x,mu,sigma)(mu=0,sigma=1时可以省略)

2. 概率分布

p=normcdf(x,mu,sigma)

可用于计算概率

3. 逆概率分布

x=norminv(a,mu,sigma); %即可求出x,使得P{X＜x}=a,可用于求分位数

4. 均值和方差

[m,v]=normstat(mu,sigma)

5. 随机数生成

M=normrnd(mu,sigma,m,n) 即可生成m*n阶的正态分布随机数矩阵

二、频数直方图

1. 给出数组data的频数表的命令为：[N,X]=hist(data,k)

将数据分为k个小区间（当k=10时可缺省），返回数组data落在每一个区间的频数N和每一个小区间的中点x

三、正态分布的参数估计

点估计和区间估计同时可由命令

[muhat, sigmahat,muci,sigmaci]=normfit(x,alpha); % 参数估计：fit

在显著性水平alpha(当alpha为0.05时可缺省)下估计数据x的参数

返回值muhat是x的均值的点估计值

sigmahat是x标准差的点估计值

muci是x的均值的区间估计值

sigma是x标准差的区间估计值