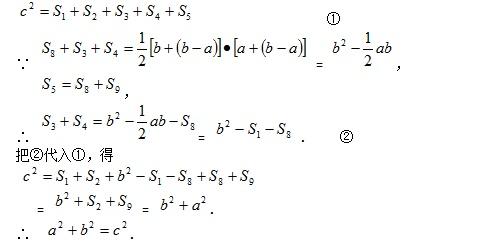初中数学：勾股定理的16种证明

勾股定理的十六种的证明方法是初中数学几何证明的基础，为了更好的学习勾股定理的证明奠定基础，极客数学帮下面整理分享十六种证明方法，我们一起来看看吧。

勾股定理的证明方法1（课本的证明方法）

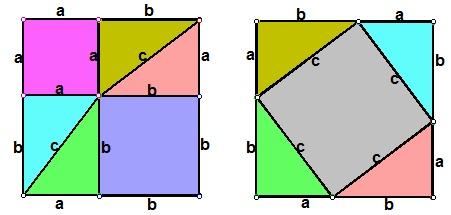
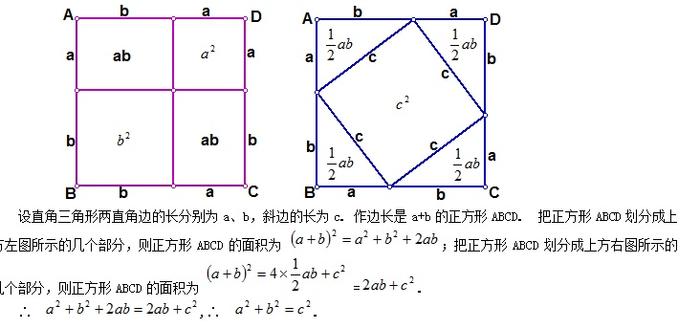
做8个全等的直角三角形，设它们的两条直角边长分别为a、b，斜边长为c，再做三个边长分别为a、b、c的正方形，把它们像上图那样拼成两个正方形.

从图上可以看到，这两个正方形的边长都是a + b，所以面积相等.即a的平方加b的平方，加4乘以二分之一ab等于c的平方，加4乘以二分之一ab，整理得a的平方加b的平方等于c的平方。

勾股定理的证明方法2（邹元治证明）

以a、b为直角边，以c为斜边做四个全等的直角三角形，则每个直角三角形的面积等于二分之一ab.把这四个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上，B、F、C三点在一条直线上，C、G、D三点在一条直线上.

∵ RtΔHAE ≌ RtΔEBF,

∴ ∠AHE = ∠BEF.

∵ ∠AEH + ∠AHE = 90º,

∴ ∠AEH + ∠BEF = 90º.

∴ ∠HEF = 180º―90º= 90º.

∴四边形EFGH是一个边长为c的

正方形.它的面积等于c2.

∵ RtΔGDH ≌ RtΔHAE,

∴ ∠HGD = ∠EHA.

∵ ∠HGD + ∠GHD = 90º,

∴ ∠EHA + ∠GHD = 90º.

又∵ ∠GHE = 90º,

∴ ∠DHA = 90º+ 90º= 180º.

∴ ABCD是一个边长为a + b的正方形，它的面积等于a+b的平方。

∴a加b的平方等于4乘二分之一ab，加上c的平方。.

∴a的平方加b的平方等于c的平方。

勾股定理的证明方法3（赵爽证明）

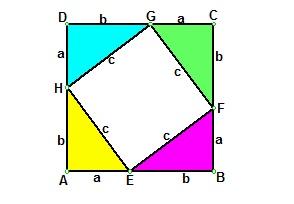
以a、b为直角边（b>a），以c为斜边作四个全等的直角三角形，则每个直角三角形的面积等于二分之一ab。把这四个直角三角形拼成如图所示形状。

∵ RtΔDAH ≌ RtΔABE,

∴ ∠HDA = ∠EAB.

∵ ∠HAD + ∠HAD = 90º，

∴ ∠EAB + ∠HAD = 90º，

∴ ABCD是一个边长为c的正方形，它的面积等于c2.

∵ EF = FG =GH =HE = b―a ,

∠HEF = 90º.

∴ EFGH是一个边长为b―a的正方形，它的面积等于b减a的平方。

∴ 4乘二分之一ab加上，b减a的平方等于c的平方。

∴ a^2+b^2=c^2(说明a^2为a的平方)。

勾股定理的证明方法4（1876年美国总统Garfield证明）

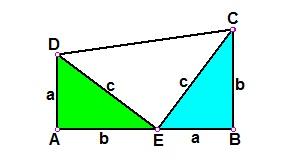
以a、b为直角边，以c为斜边作两个全等的直角三角形，则每个直角三角形的面积等于二分之一ab。把这两个直角三角形拼成如图所示形状，使A、E、B三点在一条直线上.

∵ RtΔEAD ≌ RtΔCBE,

∴ ∠ADE = ∠BEC.

∵ ∠AED + ∠ADE = 90º,

∴ ∠AED + ∠BEC= 90º.

∴ ∠DEC = 180º―90º= 90º.

∴ ΔDEC是一个等腰直角三角形，

它的面积等于二分之一c^2.

又∵ ∠DAE = 90º, ∠EBC = 90º,

∴ AD∥BC.

∴ ABCD是一个直角梯形，它的面积等于1/2(a+b)^2.

∴1/2(a+b)^2=2x1/2ab+1/2c^2..

∴a^2+b^2=c^2.

勾股定理的证明方法5（梅文鼎证明）

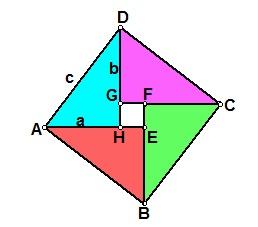
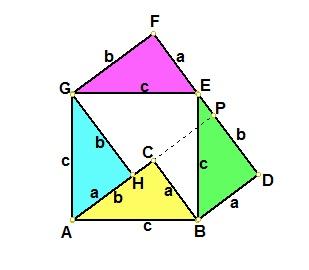
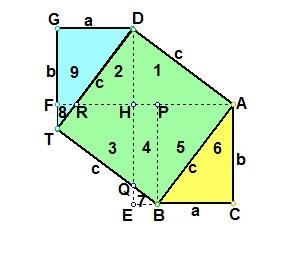
做四个全等的直角三角形，设它们的两条直角边长分别为a、b ，斜边长为c.把它们拼成如图那样的一个多边形，使D、E、F在一条直线上.过C作AC的延长线交DF于点P.

∵ D、E、F在一条直线上,且RtΔGEF ≌ RtΔEBD,

∴ ∠EGF = ∠BED，

∵ ∠EGF + ∠GEF = 90°，

∴ ∠BED + ∠GEF = 90°，

∴ ∠BEG =180º―90º= 90º.

又∵ AB = BE = EG = GA = c，

∴ ABEG是一个边长为c的正方形.

∴ ∠ABC + ∠CBE = 90º.

∵ RtΔABC ≌ RtΔEBD,

∴ ∠ABC = ∠EBD.

∴ ∠EBD + ∠CBE = 90º.

即 ∠CBD= 90º.

又∵ ∠BDE = 90º，∠BCP = 90º，

BC = BD = a.

∴ BDPC是一个边长为a的正方形.

同理，HPFG是一个边长为b的正方形.

设多边形GHCBE的面积为S，则

a^2+b^2=S+2 x 1/2xab

c^2=S+2x1/2 x ab

∴ a^2+b^2=c^2.

勾股定理的证明方法6（项明达证明）

做两个全等的直角三角形，设它们的两条直角边长分别为a、b（b>a） ，斜边长为c.再做一个边长为c的正方形.把它们拼成如图所示的多边形，使E、A、C三点在一条直线上.

过点Q作QP∥BC，交AC于点P.

过点B作BM⊥PQ，垂足为M；再过点

F作FN⊥PQ，垂足为N.

∵ ∠BCA = 90º，QP∥BC，

∴ ∠MPC = 90º，

∵ BM⊥PQ，

∴ ∠BMP = 90º，

∴ BCPM是一个矩形，即∠MBC = 90º.

∵ ∠QBM + ∠MBA= ∠QBA = 90º，

∠ABC + ∠MBA= ∠MBC = 90º，

∴ ∠QBM = ∠ABC，

又∵ ∠BMP = 90º，∠BCA = 90º，BQ = BA = c，

∴ RtΔBMQ ≌ RtΔBCA.

同理可证RtΔQNF ≌ RtΔAEF.

从而将问题转化为【证法4】（梅文鼎证明）.

勾股定理的证明方法7（欧几里得证明）

做三个边长分别为a、b、c的正方形，把它们拼成如图所示形状，使H、C、B三点在一条直线上，连结BF、CD.过C作CL⊥DE，交AB于点M，交DE于点L.

∵ AF = AC，AB = AD，

∠FAB = ∠GAD，

∴ ΔFAB ≌ ΔGAD，

∵ ΔFAB的面积等于1/2乘a^2，

ΔGAD的面积等于矩形ADLM

的面积的一半，

∴矩形ADLM的面积 =a^2.

同理可证，矩形MLEB的面积 =b^2.

∵正方形ADEB的面积

=矩形ADLM的面积 +矩形MLEB的面积

∴c^2=a^2+b^2，即a^2+b^2=c^2.

勾股定理的证明方法8（利用相似三角形性质证明）

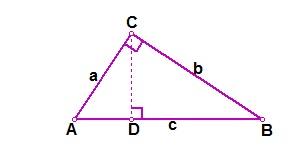
如图，在RtΔABC中，设直角边AC、BC的长度分别为a、b，斜边AB的长为c，过点C作CD⊥AB，垂足是D.

在ΔADC和ΔACB中，

∵ ∠ADC = ∠ACB = 90º，

∠CAD = ∠BAC，

∴ ΔADC ∽ ΔACB.

AD∶AC = AC ∶AB，

即 AC^2=AD·AB.

同理可证，ΔCDB ∽ ΔACB，从而有BC^2=BD·AB.

∴AC^2+BC^2=(AD+DB)·AB=AB^2 ，即a^2+b^2=c^2.

勾股定理的证明方法9（杨作玫证明）

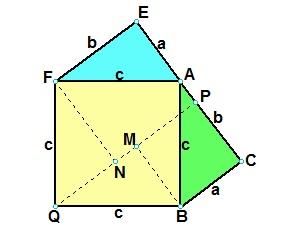
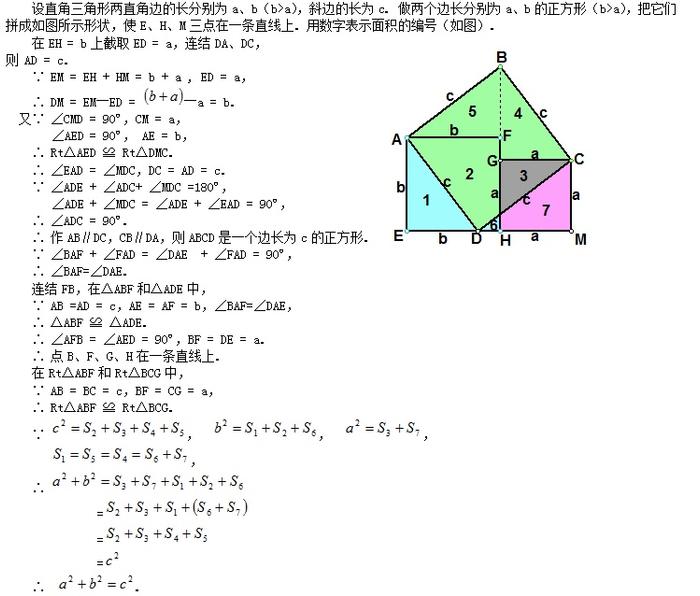
做两个全等的直角三角形，设它们的两条直角边长分别为a、b（b>a），斜边长为c.再做一个边长为c的正方形.把它们拼成如图所示的多边形.过A作AF⊥AC，AF交GT于F，AF交DT于R.过B作BP⊥AF，垂足为P.过D作DE与CB的延长线垂直，垂足为E，DE交AF于H.

∵ ∠BAD = 90º，∠PAC = 90º，

∴ ∠DAH = ∠BAC.

又∵ ∠DHA = 90º，∠BCA = 90º，

AD = AB = c，

∴ RtΔDHA ≌ RtΔBCA.

∴ DH = BC = a，AH = AC = b.

由作法可知， PBCA是一个矩形，

所以 RtΔAPB ≌ RtΔBCA.即PB =

CA = b，AP= a，从而PH = b―a.

∵ RtΔDGT ≌ RtΔBCA ,

RtΔDHA ≌ RtΔBCA.

∴ RtΔDGT ≌ RtΔDHA.

∴ DH = DG = a，∠GDT = ∠HDA.

又∵ ∠DGT = 90º，∠DHF = 90º，

∠GDH = ∠GDT + ∠TDH = ∠HDA+ ∠TDH = 90º，

∴ DGFH是一个边长为a的正方形.

∴ GF = FH = a.TF⊥AF，TF = GT―GF = b―a.

∴ TFPB是一个直角梯形，上底TF=b―a，下底BP= b，高FP=a +（b―a）.

用数字表示面积的编号（如图），则以c为边长的正方形的面积为

勾股定理的证明方法10（李锐证明）

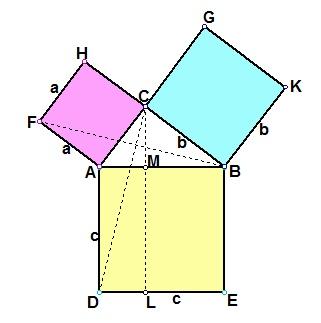
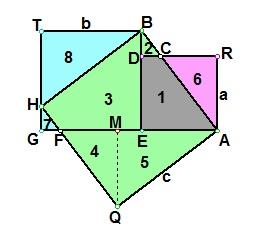
设直角三角形两直角边的长分别为a、b（b>a），斜边的长为c.做三个边长分别为a、b、c的正方形，把它们拼成如图所示形状，使A、E、G三点在一条直线上.用数字表示面积的编号（如图）.

∵ ∠TBE = ∠ABH = 90º，

∴ ∠TBH = ∠ABE.

又∵ ∠BTH = ∠BEA = 90º，

BT = BE = b，

∴ RtΔHBT ≌ RtΔABE.

∴ HT = AE = a.

∴ GH = GT―HT = b―a.

又∵ ∠GHF + ∠BHT = 90º，

∠DBC + ∠BHT = ∠TBH + ∠BHT = 90º，

∴ ∠GHF = ∠DBC.

∵ DB = EB―ED = b―a，

∠HGF = ∠BDC = 90º，

勾股定理的证明方法11（利用切割线定理证明）

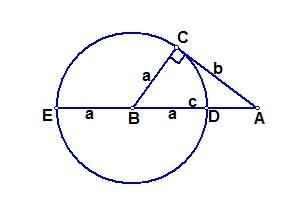
在RtΔABC中，设直角边BC = a，AC = b，斜边AB = c.如图，以B为圆心a为半径作圆，交AB及AB的延长线分别于D、E，则BD = BE = BC = a.因为∠BCA = 90º，点C在⊙B上，所以AC是⊙B的切线.由切割线定理，得

AC^2=AE·AD

=(AB+BE)(AB-BD)

=(c+a)(c-a)

=c^2-a^2,

即b^2=c^2-a^2,

∴ a^2+b^2=c^2

勾股定理的证明方法12（利用多列米定理证明）

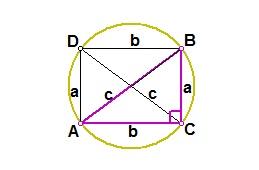
在RtΔABC中，设直角边BC = a，AC = b，斜边AB = c（如图）.过点A作AD∥CB，过点B作BD∥CA，则ACBD为矩形，矩形ACBD内接于一个圆.根据多列米定理，圆内接四边形对角线的乘积等于两对边乘积之和，有

AB·DC=AD·BC+AC·BD，

∵ AB = DC = c，AD = BC = a，

AC = BD = b，

∴AB^2=BC^2+AC^2，即c^2=a^2+b^2，

∴a^2+b^2=c^2.

勾股定理的证明方法13（作直角三角形的内切圆证明）

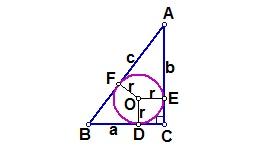
在RtΔABC中，设直角边BC = a，AC = b，斜边AB = c.作RtΔABC的内切圆⊙O，切点分别为D、E、F（如图），设⊙O的半径为r.

∵ AE = AF，BF = BD，CD = CE，

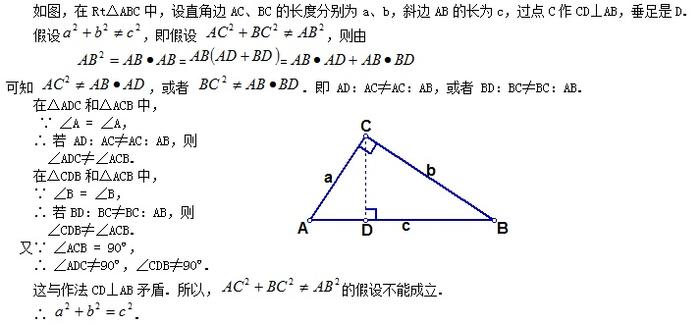
勾股定理的证明方法14（利用反证法证明）

勾股定理的证明方法15（辛卜松证明）

勾股定理的证明方法16（陈杰证明）