| 【经典面试题】实现平方根函数sqrt | 您所在的位置:网站首页 › python定义一个求平方根的函数 › 【经典面试题】实现平方根函数sqrt |
【经典面试题】实现平方根函数sqrt
|
/*************************************************************************
* 作者:xusiwei1236([email protected])
* 出处:http://blog.csdn.net/xusiwei1236
* 声明:转载请注明出处,请勿用于商用.
* 对本文所涉及的主题如有任何观点、想法,欢迎交流(email或评论)
************************************************************************/
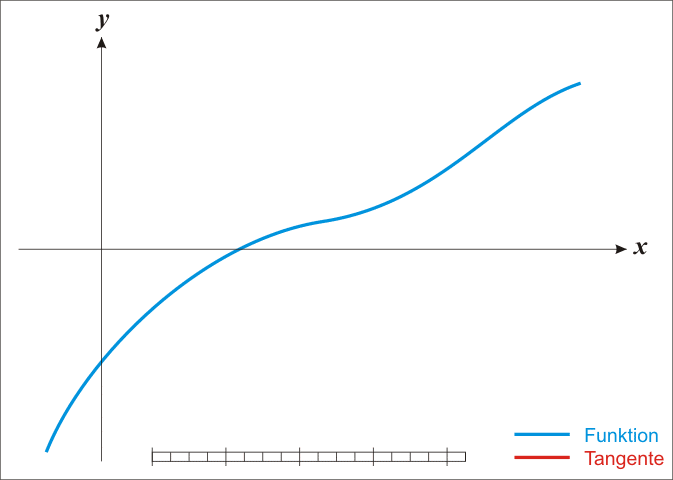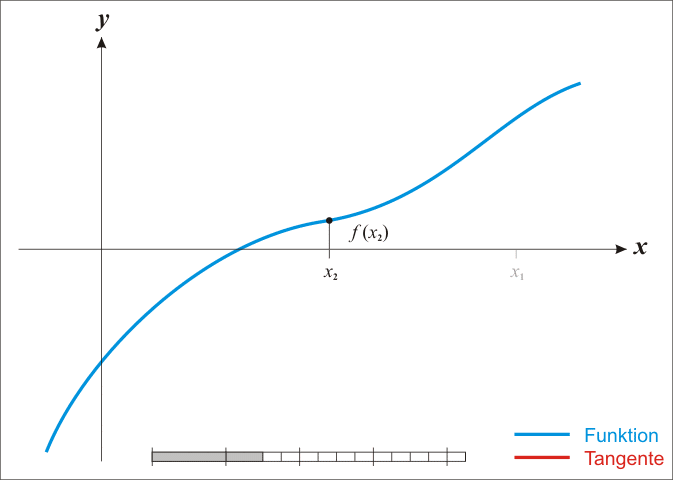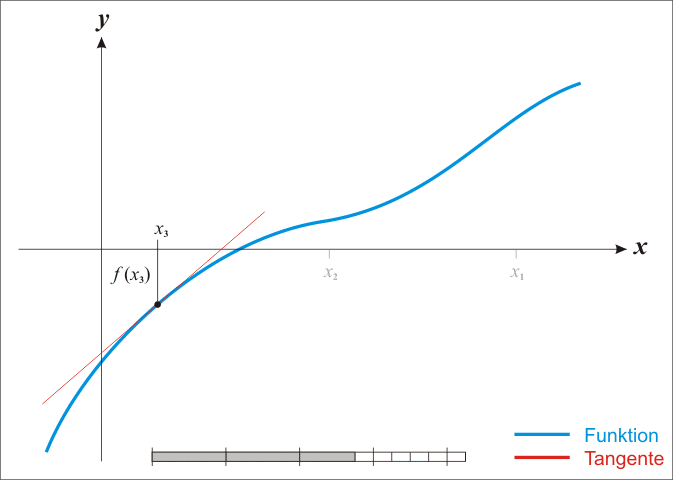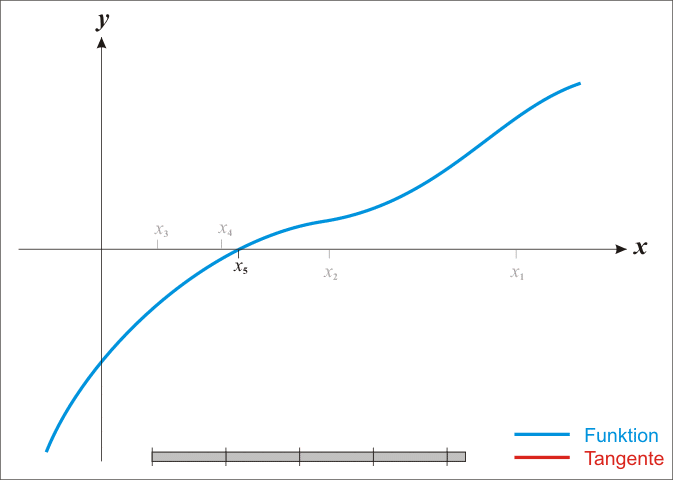
本文将从一道经典的面试题说起:实现平方根函数,不得调用其他库函数。 函数原型声明如下: double Sqrt(double A); 二分法 二分法的概念求 二分法的过程可用下图表示:
初始区间的选定 可见,若要用“二分法”求方程 取f(A)=A?不行,因为它不能始终保证
从图像可知,当A>1时,才有 同时可知,sqrt(A)在原点处的切线平行于y轴,所以找不到常数项为零的多项式f(A),使得 据此,可推出一个 令 显然,当
为了说明二分法的误差,需要借助一个定理。 零点定理:若f(x)在(a,b)连续,且f(a)f(b) 2*DBL_EPSILON) { // sometimes dead cycle when m==a or m==b. for(;;) { m = (b + a)/2; if( m-a < DBL_EPSILON || b-m < DBL_EPSILON ) break; if( (m*m - A) * (a*a - A) < 0 ) b = m; else a = m; } return m; } 需要注意的是: 初始上界是A+0.25,而不是A;double型的精度DBL_EPSILON,不能随意指定;牛顿迭代法 下面介绍另一种应用广泛的方法——牛顿迭代法。 牛顿法的概念牛顿迭代法是迭代法的一种,它的迭代格式为: 牛顿法具有明显的几何意义,x[k+1]正是曲线在x[k]处的切线与x轴的交点的横坐标。因此,牛顿法也称切线法。 来自Wikipedia的一个动态图很好的解释了这种几何意义:
牛顿法初值的选定 在开始牛顿迭代法之前,需要选定一个d迭代初值x0。根据前文分析,求sqrt(A),也可以取x0 = A+0.25; 牛顿法sqrt根据牛顿法,求 离实现牛顿法还差关键一步:迭代的结束条件。 在不知道误差公式,且要求误差尽可能小情况下可以使用另一种方法——限定f(x)=0的误差(此法仅限于不给误差范围,且要求误差尽可能小时使用)。
据此,实现的sqrt如下: double Sqrt(double A) { double x0 = A + 0.25, x1, xx = x0; for(;;) { x1 = (x0*x0 + A) / (2*x0); if(fabs(x1 - x0) 5*DBL_EPSILON是因为,x的误差在2*DBL_EPSILON范围内,所以x*x的误差就在4*DBL_EPSILON范围,考虑到浮点乘法的精度丢失,所以为5*DBL_EPSILON。 迭代法的理论基础 迭代格式收敛的前提迭代法在进行“迭代”之前,需将原方程 整个过程的所有x构成了数列: 所以,迭代法能够求得近似解的前提是 其中x*为方程 迭代法收敛的前提是 是否有更简单的方法判定迭代格式收敛?当然有,下面介绍一个定理能够简便的判定迭代格式是否收敛,同时也能判定误差。 定理 迭代格式收敛条件(Vipschitz条件) 若迭代函数 ①一阶导数连续; ②当x∈[a, b]时,有 ③存在常数 则 方程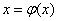 有唯一根x*;对任意x0∈[a, b],迭代格式 有唯一根x*;对任意x0∈[a, b],迭代格式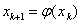 收敛,且 收敛,且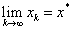 ; ;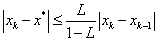 ,(事后误差估计); ,(事后误差估计);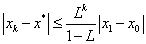 ,(事前误差估计); ,(事前误差估计);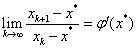
定理应用 下面以求 1)判断收敛
它的导函数为:
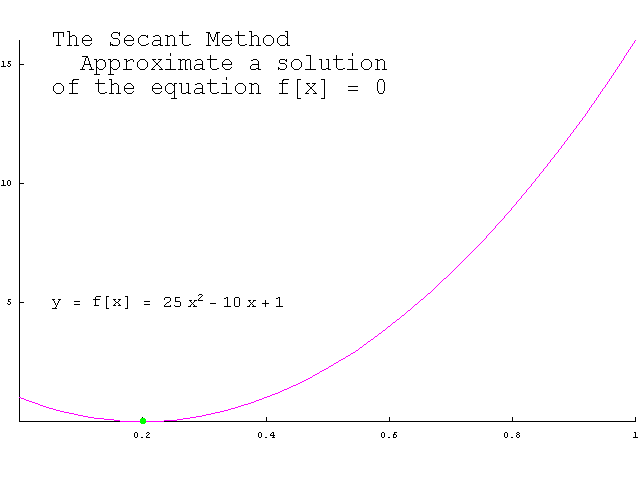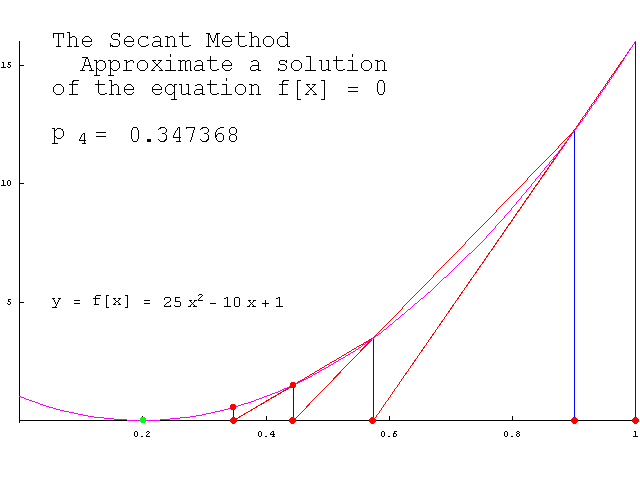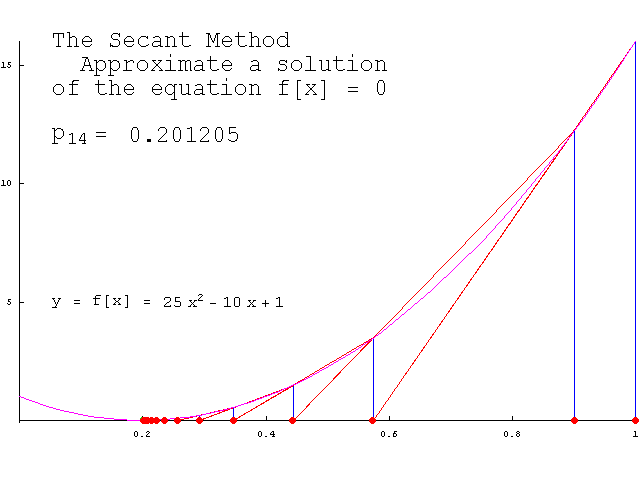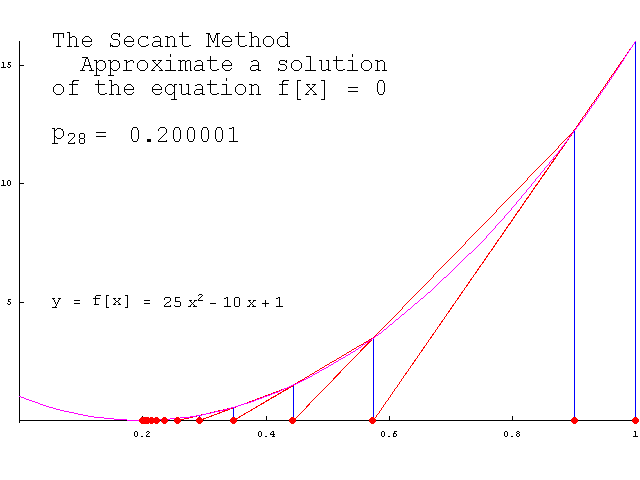
在[0, A+0.25]区间内它显然连续,且存在L=1/2使得 2)估计误差(迭代次数) 有了L = 1/2;就可以根据定理估算: ①给定误差情况下,需要迭代几次? ②给定迭代次数,最终近似解的误差? 比如,假设题目要求的精度是:小数点后2位(精确到0.01),那么误差要小于0.01 / 2 = 0.005;只需根据初值x0和第一次迭代结果x1和定理的结论4,便可算出迭代次数k,这里不再罗列(公式编辑起来比较麻烦)。 同样,根据x0,x1和结论4,也可以很方便的算出第k次迭代的误差; 推广——一般方程求近似解 本文指出的二分法、牛顿迭代法是求解方程近似解的常见方法,不仅仅限于求sqrt,但在本文所实现的sqrt程序的基础上,可以很快实现求解其他方程的程序。 二分法比如,如下程序段就是二分法求解任意方程f(x)=0的程序: double bisection(double (*f)(double), double a, double b, double eps) { double m; assert( f != NULL && f(a) * f(b) < 0.0 && (b-a) > DBL_EPSILON); // (b-a) > DBL_EPSILON 即 b > a while( b - a > eps ) { m = (a + b)/2; if( f(m) * f(a) < 0.0 ) b = m; else a = m; } return m; }这个程序较为“好用”,只需给出函数f,区间[a, b],误差eps即可。 迭代法 同样,有了对迭代法的理论基础,我们知道了迭代法的误差如何估计。下面是迭代法求一般方程的近似解的程序: double iteration(double (*g)(double), double L, double x0, double eps) { double x1, t = L/(1 - L);; for(;;) { x1 = g(x0); if(fabs( t*(x1-x0) ) < eps) break; x0 = x1; } return x1; }这个函数没有上面的二分法那么好用,因为需要根据f(x)自行推出递推函数g,并根据递推函数的倒数找到一个常数L;再给出初值x0,误差eps。 割线法 事实上,真正通用的牛顿法很难实现,因为从f(x)推出它的导函数f1(x)的过程并不容易。割线法可以避免这一难题,它使用差商:
来代替牛顿公式中的导数f'(xk),于是得到了“割线法”迭代公式:
割线法和牛顿法类似,有着明确的几何意义。下面的gif动态地展示了割线法的几何意义(若没有看到动画效果可尝试刷新本页):
(图片来自Dr. Mathews的教案,) 割线法求一般方程的近似解的程序如下: double secant(double (*f)(double), double x0, double x1, double eps) { double x2; for(;;) { x2 = x1 - f(x1)/(f(x1) - f(x0))*(x1 - x0); if( fabs(x2-x1) < eps ) break; x0 = x1; x1 = x2; } return x2; }这个函数也很好使用,只需给出f,[a, b],eps即可。 割线法实现的sqrt如下: double Sqrt(double A) { double x0 = 0, x1 = A+0.25, x2; double fx0 = x0*x0 - A, fx1 = x1*x1 - A; for(;;) { x2 = x1 - fx1*(x1-x0) / (fx1-fx0); if(fabs(x2 - x1) < 2*DBL_EPSILON) break; x0 = x1; fx0 = fx1; x1 = x2; fx1 = x2*x2 - A; } return x2; } 收敛速度对比对于sqrt的实现,本文介绍了三种方法,分别为:二分法,牛顿法,割线法; 二分法的收敛速度对于二分法,相邻两次的误差ek+1和ek间的关系为:
由此,我们可以引申出迭代法收敛速度的判定标准: 定义 迭代法收敛的阶 设序列{xk}收敛于x*,并记ek = xk - x*,如果存在非负常数c和正常数p,使得
则称序列{xk}是p阶收敛的。当p=1,且0 |
【本文地址】
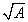 ,等价于求方程
,等价于求方程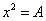 的非负根(解)。求解方程近似根的方法中,最直观、最简单的方法是二分法。“二分法”算法步骤如下:
的非负根(解)。求解方程近似根的方法中,最直观、最简单的方法是二分法。“二分法”算法步骤如下: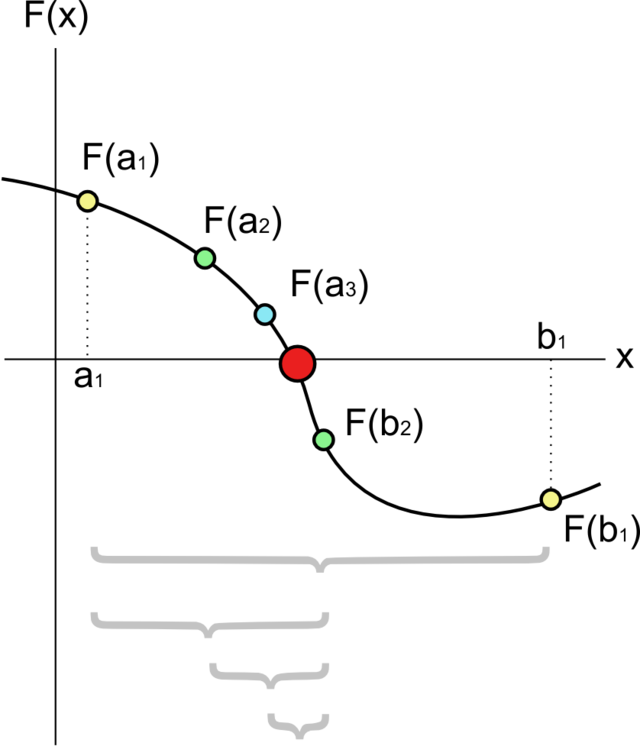
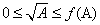 ?
?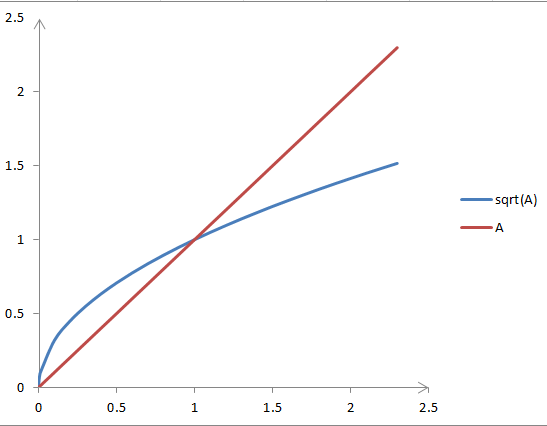
 。若用A作为第一步的上界,则在A小于1时,将无法得到正确结果。
。若用A作为第一步的上界,则在A小于1时,将无法得到正确结果。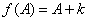 ,使得
,使得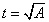 ,则t>=0,
,则t>=0,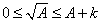 , 等价于
, 等价于 ,即
,即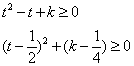
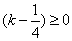 时,上式成立,所以k可以取[1/4, +∞)的任意值,不妨取k=1/4,即有
时,上式成立,所以k可以取[1/4, +∞)的任意值,不妨取k=1/4,即有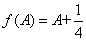 ,使得
,使得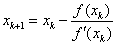
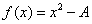 的非负根,
的非负根,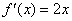 , 所以,此时的牛顿递推式为:
, 所以,此时的牛顿递推式为: 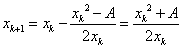
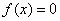 改写成
改写成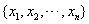 (迭代序列),数列的递推式即
(迭代序列),数列的递推式即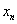 ;
;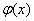 满足:
满足: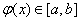 ;
;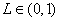 ,使得
,使得 ;
;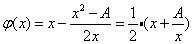
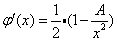
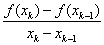
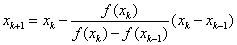
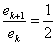 ,
,