【运筹学】运输规划、表上作业法总结 ( 运输规划模型

参考博客 :

将 两个产地 A 1 \rm A_1 A1​ , A 2 \rm A_2 A2​ 的物品运往 三个销售地 B 1 \rm B_1 B1​ , B 2 \rm B_2 B2​ , B 3 \rm B_3 B3​ ,

各地的 产量 , 销量 ,

各个产地 运往 各个销售地 的每件物品的运费如下图所示 :

A 1 , A 2 \rm A_1 , A_2 A1​,A2​ 的产量之和是 500 500 500 ,

B 1 , B 2 , B 3 \rm B_1 , B_2 , B_3 B1​,B2​,B3​ 的总的销量之和是 500 500 500 ,

上述产量之和等于销量之和 , 是产销平衡的 ;

不同的产地运往不同的销地 , 运费不同 , 如何合理安排运输 , 能使总运费最少 ;

这里存在一个产销平衡问题 : 总产量 = 总销量 = 500 500 500 ;

假设变量 :

A 1 \rm A_1 A1​ 产地运往 B 1 \rm B_1 B1​ 产地的产品数量是 x 1 \rm x_1 x1​ ,

A 1 \rm A_1 A1​ 产地运往 B 2 \rm B_2 B2​ 产地的产品数量是 x 2 \rm x_2 x2​ ,

A 1 \rm A_1 A1​ 产地运往 B 3 \rm B_3 B3​ 产地的产品数量是 x 3 \rm x_3 x3​ ,

A 2 \rm A_2 A2​ 产地运往 B 1 \rm B_1 B1​ 产地的产品数量是 x 4 \rm x_4 x4​ ,

A 2 \rm A_2 A2​ 产地运往 B 2 \rm B_2 B2​ 产地的产品数量是 x 5 \rm x_5 x5​ ,

A 2 \rm A_2 A2​ 产地运往 B 3 \rm B_3 B3​ 产地的产品数量是 x 6 \rm x_6 x6​ ;

存在以下等式约束 :

A 1 \rm A_1 A1​ 的产量 x 1 + x 2 + x 3 = 200 \rm x_1 + x_2 + x_3 = 200 x1​+x2​+x3​=200 ;

A 2 \rm A_2 A2​ 的产量 x 4 + x 5 + x 6 = 300 \rm x_4 + x_5 + x_6 = 300 x4​+x5​+x6​=300 ;

B 1 \rm B_1 B1​ 的销量 x 1 + x 4 = 150 \rm x_1 + x_4 = 150 x1​+x4​=150 ;

B 2 \rm B_2 B2​ 的销量 x 2 + x 5 = 150 \rm x_2 + x_5= 150 x2​+x5​=150 ;

B 3 \rm B_3 B3​ 的销量 x 3 + x 6 = 200 \rm x_3 + x_6= 200 x3​+x6​=200 ;

变量约束 : 每个变量肯定大于等于 0 ;

x 1 , x 2 , x 3 , x 4 , x 5 , x 6 ≥ 0 \rm x_1, x_2, x_3 , x_4 , x_5 , x_6 \geq 0 x1​,x2​,x3​,x4​,x5​,x6​≥0

目标函数 : 目的是为了使运费最小 ;

m i n W = 6 x 1 + 4 x 2 + 6 x 3 + 6 x 4 + 5 x 5 + 5 x 6 \rm minW = 6x_1 + 4x_2 + 6x_3 + 6x_4 + 5x_5 + 5x_6 minW=6x1​+4x2​+6x3​+6x4​+5x5​+5x6​

上述的目标函数与约束方程都是线性的 , 因此该规划是线性规划 ;

最终的线性规划如下 :

m i n W = 6 x 1 + 4 x 2 + 6 x 3 + 6 x 4 + 5 x 5 + 5 x 6 s . t { x 1 + x 2 + x 3 = 200 x 4 + x 5 + x 6 = 300 x 1 + x 4 = 150 x 2 + x 5 = 150 x 3 + x 6 = 200 x 1 , x 2 , x 3 , x 4 , x 5 , x 6 ≥ 0 \begin{array}{lcl} \rm minW = 6x_1 + 4x_2 + 6x_3 + 6x_4 + 5x_5 + 5x_6 \\\\ \rm s.t\begin{cases} \rm x_1 + x_2 + x_3 = 200 \\\\ \rm x_4 + x_5 + x_6 = 300 \\\\ \rm x_1 + x_4 = 150 \\\\ \rm x_2 + x_5= 150 \\\\ \rm x_3 + x_6= 200 \\\\ \rm x_1, x_2, x_3 , x_4 , x_5 , x_6 \geq 0 \end{cases}\end{array} minW=6x1​+4x2​+6x3​+6x4​+5x5​+5x6​s.t⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​x1​+x2​+x3​=200x4​+x5​+x6​=300x1​+x4​=150x2​+x5​=150x3​+x6​=200x1​,x2​,x3​,x4​,x5​,x6​≥0​​

使用单纯形法对上述规划求解即可得到最优解 ;

单纯形法解线性规划最优解过程 :

① 基可行解 : 先找到一个 初始基可行解 ;

② 检验数 : 计算检验数 , 判定当前基可行解是否是 最优解 ;

③ 迭代 : 根据检验数确定 入基变量 , 根据入基变量系数计算 出基变量 , 然后进行 同解变换 , 生成新的单纯形表 , 继续计算检验数 ;

首先确定基是多少 , 将上述线性规划 , 转为标准形 , 约束方程的系数矩阵 A m × n \rm A_{m \times n} Am×n​ 是 m × n \rm m \times n m×n 矩阵 , n ≥ m \rm n \geq m n≥m , n \rm n n 是变量个数 , m \rm m m 是约束方程个数 ,

假设 A m × n \rm A_{m \times n} Am×n​ 矩阵是行满秩的 , 即秩为 m \rm m m , 约束方程个数为 m \rm m m , 上述运输问题的约束方程个数是 5 5 5 个 ;

上述运输问题的系数矩阵为 : 5 5 5 个约束方程对应的是 5 × 6 \rm 5 \times 6 5×6 矩阵 ;

( 1 1 1 0 0 0 0 0 0 1 1 1 1 0 0 1 0 0 0 1 0 0 1 0 0 0 1 0 0 1 ) \begin{pmatrix} \quad 1 \quad 1 \quad 1 \quad 0 \quad 0 \quad 0 \quad \\\\ \quad 0 \quad 0 \quad 0 \quad 1 \quad 1 \quad 1 \quad \\\\ \quad 1 \quad 0 \quad 0 \quad 1 \quad 0 \quad 0 \quad \\\\ \quad 0 \quad 1 \quad 0 \quad 0 \quad 1 \quad 0 \quad \\\\ \quad 0 \quad 0 \quad 1 \quad 0 \quad 0 \quad 1 \quad \end{pmatrix} ⎝⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎜⎛​111000000111100100010010001001​⎠⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎟⎞​

运输问题约束方程的 系数矩阵都是由 0 0 0 或 1 1 1 组成 的 , 这种矩阵称为 稀疏矩阵 , 稀疏矩阵的计算要远远比正常的矩阵更简单 ;

针对运输问题 , 存在一个简化版的单纯形法 ;

简化版的单纯形法与单纯形法的框架基本类似 , 也需要按照 ① 初始基可行解 , ② 最优解判定 , ③ 迭代 , 步骤进行计算 ;

运输规划中 , 如果产量 = 销量 , 则 产销平衡 ;

如果 产量 ≥ \geq ≥ 销量 , 或 产量 ≤ \leq ≤ 销量 , 则 产销不平衡 ;

产量 = = = 销量 , 销量可以全部满足 , 产量可以满足 ,

产量的约束方程是 等式 ;

销量的约束方程是 等式 ;

产量 ≥ \geq ≥ 销量 , 销量可以全部满足 , 产量有些地方就有剩余的 ,

产量的约束方程就是 大于等于不等式 ;

销量的约束方程仍然是 等式 ;

产量 ≤ \leq ≤ 销量 , 产量可以全部满足 , 销量有些地方就有剩余的 ,

产量的约束方程仍然是 等式 ;

销量的约束方程仍然就是 小于等于不等式 ;

参考博客 :

运输规划问题数学模型基变量数定理 :

假设有 m \rm m m 个产地 , n \rm n n 个销地 , 并且 产销平衡 , 其基变量数为 m + n − 1 \rm m + n - 1 m+n−1 ;

m \rm m m 个产地 , n \rm n n 个销地 , 变量个数是 m × n \rm m \times n m×n 个 ;

m \rm m m 个产地 , n \rm n n 个销地 , 约束方程个数是 m + n \rm m + n m+n 个 , 这些约束方程中 , 有一个是多余的 , 最本质的方程最多有 m + n − 1 \rm m + n - 1 m+n−1 个 ;

任意删掉一个约束方程 , 就不再有多余的方程了 ;

确定约束方程个数后 , 就确定了基矩阵的秩 , 根据单纯形法的基本流程 , 第一步找初始基可行解 , 可行基就知道找什么样的可行基了 ;

单纯形法解线性规划最优解过程 :

① 基可行解 : 先找到一个 初始基可行解 ;

② 检验数 : 计算检验数 , 判定当前基可行解是否是 最优解 ;

③ 迭代 : 根据检验数确定 入基变量 , 根据入基变量系数计算 出基变量 , 然后进行 同解变换 , 生成新的单纯形表 , 继续计算检验数 ;

运输问题线性规划 本质也是线性规划 , 是特殊的线性规划 , 其 最优解 可以使用 单纯形法 求得 ;

运输问题是线性规划中比较简单的模型 , 其系数矩阵中的元素都是 0 , 1 0,1 0,1 , 是稀疏矩阵 , 可以使用简化版的单纯形法求最优解 , 该方法称为 " 表上作业法 " ;

m \rm m m 个产地 , n \rm n n 个销地 , 变量个数是 m × n \rm m \times n m×n 个 ;

m \rm m m 个产地 , n \rm n n 个销地 , 约束方程个数是 m + n \rm m + n m+n 个 , 这些约束方程中 , 有一个是多余的 , 最本质的方程最多有 m + n − 1 \rm m + n - 1 m+n−1 个 ;

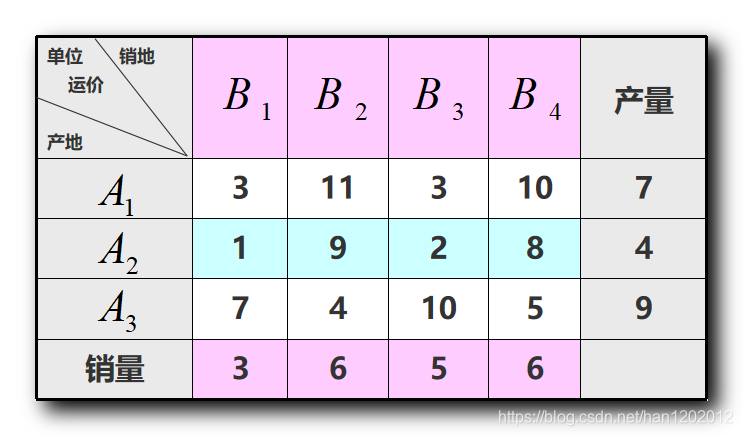
第一步 , 开始找 初始基可行解 , 基变量个数是 m + n − 1 \rm m + n - 1 m+n−1 个 , 基矩阵的秩是 m + n − 1 \rm m + n - 1 m+n−1 ;

求解基可行解时 , 非基变量取值 0 0 0 , 基变量允许非 0 0 0 变量 , 找 m + n − 1 \rm m + n - 1 m+n−1 个基变量 ,

第二步 , 找到一个规则 , 判断是否是最优解 ;

第三步 , 如果不是最优解 , 进行 迭代 , 如何进行迭代 ;

运输问题如下 : 下面的表格代表 3 3 3 个产地 , 4 4 4 个销地 的运输规划问题 , 表格中的内容是 某产地运往某销地的运费 ;

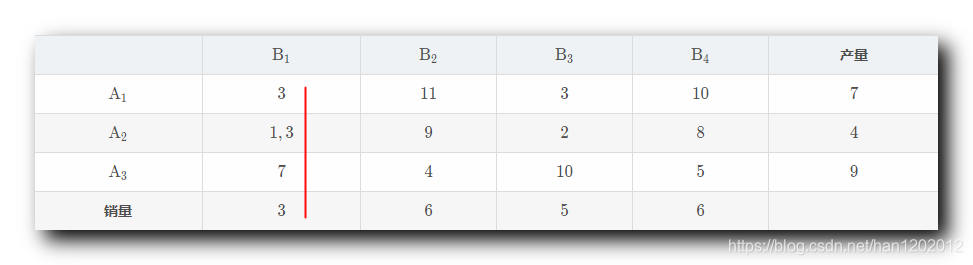
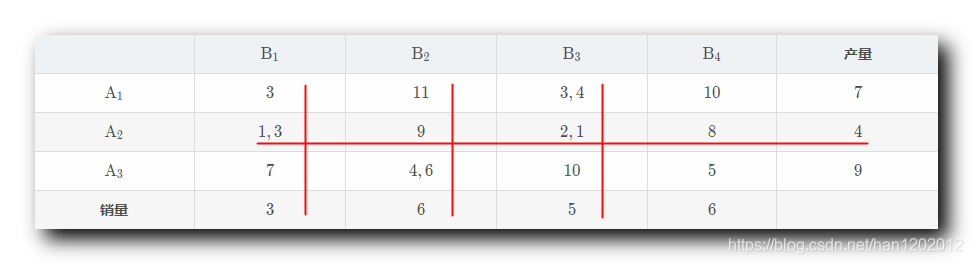
上述运输规划问题 总共有 m × n = 3 × 4 = 12 \rm m \times n = 3 \times 4 = 12 m×n=3×4=12 个变量 ;

基变量个数 = m + n − 1 = 3 + 4 − 1 = 6 \rm = m + n - 1 = 3 + 4 - 1 = 6 =m+n−1=3+4−1=6 ;

初始基可行解中需要找 6 6 6 个变量作为基变量 , 其取值是非 0 0 0 的 ; 剩余的 6 6 6 个变量是非基变量 , 取值为 0 0 0 ;

运输规划的目的是使总运费最小 ,

这里引入 最小元素法 思想 , 基本原则是 " 安排运输方案时 , 从单位成本最小的开始安排 " , 优先满足运费最小的运输 , 然后再考虑其它情况 ;

最小元素法基本思想 :

就近供应 , 从运费最小的地方开始供应 , 然后逐步供应运费稍高的地方 , 直到最终供应完毕为止 ;

每个表格中需要填写两部分 , 第一部分是 c i j \rm c_{ij} cij​ 运费 , 第二部分是变量 x i j \rm x_{ij} xij​ ;

第 1 1 1 个基变量 :

从所有 没有被划掉 的并且 没有被安排 的的运费中找到最小的 , 即 1 1 1 ; 对应表格第 2 2 2 行第 1 1 1 列 , A 2 \rm A_2 A2​ 产地运往 B 1 \rm B_1 B1​ 销地的运费 ;

产地分析 : 对于产地 A 2 \rm A_2 A2​ 来说 , 其生产 4 4 4 个 , 已经安排了 0 0 0 个 , 还可以再安排 4 4 4 个 ;

销地分析 : 对于销地 B 1 \rm B_1 B1​ 来说需求 3 3 3 个 , 已经安排了 0 0 0 个 , 还可以再安排 3 3 3 个 ;

如果要使运费最低 , 优先让运费最低的情况 , 最大量运输 , 这里直接从 A 2 \rm A_2 A2​ 向 B 1 \rm B_1 B1​ 运输 3 3 3 个产品 ;

此时 B 1 \rm B_1 B1​ 的销量已经全部消耗完毕 , 该列就不需要安排其它产地向 B 1 \rm B_1 B1​ 销地运输了 , 可以划掉这一列 , 讨论其它列的运输问题 ;

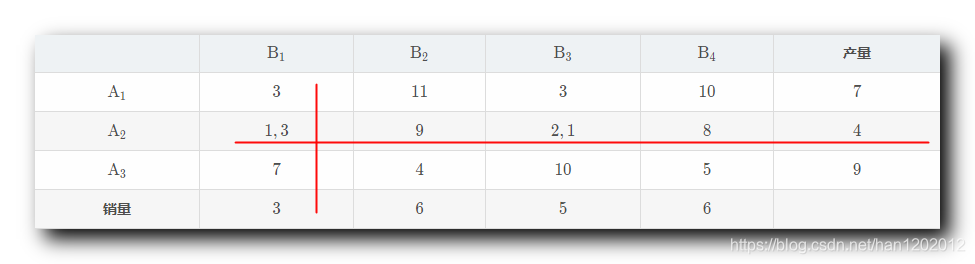
第 2 2 2 个基变量 :

从所有 没有被划掉 的并且 没有被安排 的运费中找到最小的 , 即 2 2 2 ; 对应表格第 2 2 2 行第 3 3 3 列 , A 2 \rm A_2 A2​ 产地运往 B 3 \rm B_3 B3​ 销地的运费 ;

产地分析 : 对于产地 A 2 \rm A_2 A2​ 来说 , 其生产 4 4 4 个 , 已经安排了 3 3 3 个 , 还可以再安排 1 1 1 个 ;

销地分析 : 对于销地 B 3 \rm B_3 B3​ 来说需求 5 5 5 个 , 已经安排了 0 0 0 个 , 还可以再安排 5 5 5 个 ;

如果要使运费最低 , 优先让运费最低的情况 , 最大量运输 , 这里直接从 A 2 \rm A_2 A2​ 向 B 3 \rm B_3 B3​ 运输 1 1 1 个产品 ;

此时 A 2 \rm A_2 A2​ 的产量已经全部消耗完毕 , 该行就不需要安排向其它销地运输了 , 可以划掉这一行 , 讨论其它行列的运输问题 ;

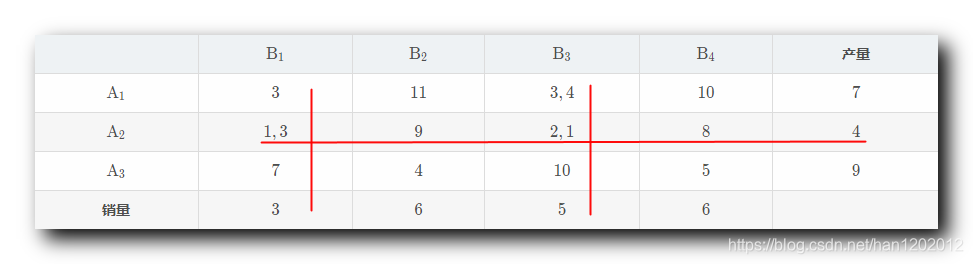
第 3 3 3 个基变量 :

从所有 没有被划掉 的并且 没有被安排 的的运费中找到最小的 , 即 3 3 3 ; 对应表格第 1 1 1 行第 3 3 3 列 , A 1 \rm A_1 A1​ 产地运往 B 3 \rm B_3 B3​ 销地的运费 ;

产地分析 : 对于产地 A 1 \rm A_1 A1​ 来说 , 其生产 7 7 7 个 , 已经安排了 0 0 0 个 , 还可以再安排 7 7 7 个 ;

销地分析 : 对于销地 B 3 \rm B_3 B3​ 来说需求 5 5 5 个 , 已经安排了 1 1 1 个 , 还可以再安排 4 4 4 个 ;

如果要使运费最低 , 优先让运费最低的情况 , 最大量运输 , 这里直接从 A 1 \rm A_1 A1​ 向 B 3 \rm B_3 B3​ 运输 4 4 4 个产品 ;

此时 B 3 \rm B_3 B3​ 的销量已经全部消耗完毕 , 该列就不需要安排向其它产地向 B 3 \rm B_3 B3​ 销地运输了 , 可以划掉这一列 , 讨论其它行列的运输问题 ;

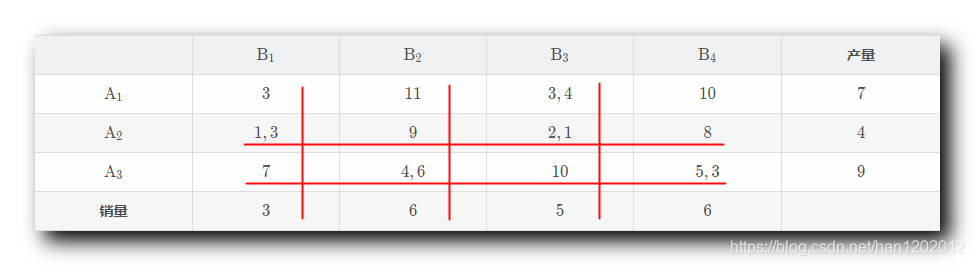
第 4 4 4 个基变量 :

从所有 没有被划掉 的并且 没有被安排 的的运费中找到最小的 , 即 4 4 4 ; 对应表格第 3 3 3 行第 2 2 2 列 , A 3 \rm A_3 A3​ 产地运往 B 2 \rm B_2 B2​ 销地的运费 ;

产地分析 : 对于产地 A 3 \rm A_3 A3​ 来说 , 其生产 9 9 9 个 , 已经安排了 0 0 0 个 , 还可以再安排 9 9 9 个 ;

销地分析 : 对于销地 B 2 \rm B_2 B2​ 来说需求 6 6 6 个 , 已经安排了 0 0 0 个 , 还可以再安排 6 6 6 个 ;

如果要使运费最低 , 优先让运费最低的情况 , 最大量运输 , 这里直接从 A 3 \rm A_3 A3​ 向 B 2 \rm B_2 B2​ 运输 6 6 6 个产品 ;

此时 B 2 \rm B_2 B2​ 的销量已经全部消耗完毕 , 该列就不需要安排向其它产地向 B 2 \rm B_2 B2​ 销地运输了 , 可以划掉这一列 , 讨论其它行列的运输问题 ;

第 5 5 5 个基变量 :

从所有 没有被划掉 的并且 没有被安排 的的运费中找到最小的 , 即 5 5 5 ; 对应表格第 3 3 3 行第 4 4 4 列 , A 3 \rm A_3 A3​ 产地运往 B 4 \rm B_4 B4​ 销地的运费 ;

产地分析 : 对于产地 A 3 \rm A_3 A3​ 来说 , 其生产 9 9 9 个 , 已经安排了 6 6 6 个 , 还可以再安排 3 3 3 个 ;

销地分析 : 对于销地 B 4 \rm B_4 B4​ 来说需求 6 6 6 个 , 已经安排了 0 0 0 个 , 还可以再安排 6 6 6 个 ;

如果要使运费最低 , 优先让运费最低的情况 , 最大量运输 , 这里直接从 A 3 \rm A_3 A3​ 向 B 4 \rm B_4 B4​ 运输 3 3 3 个产品 ;

此时 A 3 \rm A_3 A3​ 的产量已经全部消耗完毕 , 该行就不需要安排向其它销地运输了 , 可以划掉这一行 , 讨论其它行列的运输问题 ;

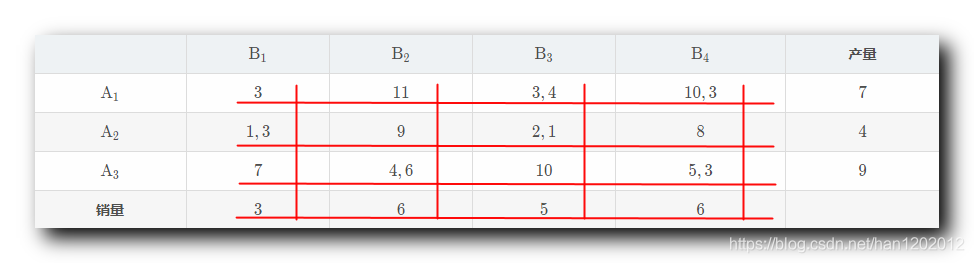
第 6 6 6 个基变量 :

从所有 没有被划掉 的并且 没有被安排 的的运费中找到最小的 , 即 10 10 10 ; 对应表格第 1 1 1 行第 4 4 4 列 , A 1 \rm A_1 A1​ 产地运往 B 4 \rm B_4 B4​ 销地的运费 ;

产地分析 : 对于产地 A 1 \rm A_1 A1​ 来说 , 其生产 7 7 7 个 , 已经安排了 4 4 4 个 , 还可以再安排 3 3 3 个 ;

销地分析 : 对于销地 B 4 \rm B_4 B4​ 来说需求 6 6 6 个 , 已经安排了 3 3 3 个 , 还可以再安排 3 3 3 个 ;

如果要使运费最低 , 优先让运费最低的情况 , 最大量运输 , 这里直接从 A 1 \rm A_1 A1​ 向 B 4 \rm B_4 B4​ 运输 3 3 3 个产品 ;

此时 A 1 \rm A_1 A1​ 的产量已经全部消耗完毕 , 该行就不需要安排向其它销地运输了 , 可以划掉这一行 , 讨论其它行列的运输问题 ;

此时 B 4 \rm B_4 B4​ 的销量已经全部消耗完毕 , 该列就不需要安排向其它产地向 B 4 \rm B_4 B4​ 销地运输了 , 可以划掉这一列 , 讨论其它行列的运输问题 ;

至此所有的行列全部划掉 , 所有的产销全部安排完毕 ;

此时找到的解就是运输问题的可行解 , 并且是基可行解 ;

基变量个数分析 : 在上述找基变量的时候 , 有 m \rm m m 行 n \rm n n 列 , 每找到一个基变量 , 或者划掉一行 , 或者划掉一列 , 最后的一个基变量同时花掉了一行一列 , 因此这里有 m + n − 1 \rm m + n - 1 m+n−1 个基变量 ;

使用 " 最小元素法 " , 属于贪婪算法 , 每次都找运费最小的优先供应 , 每个步骤的方案都是最优 , 局部最优 ,

每步最优不一定能使得全局最优 ;

" Vogel 方法 " 的核心思想就是从运价表中 , 分别计算 各行 , 各列 的 最小运费 和 次最小运费 差额 , 填写到表的 最右列 和 最下行 ;

基于如下运输问题进行分析 : 下面的表格代表 3 3 3 个产地 , 4 4 4 个销地 的运输规划问题 , 表格中的内容是 某产地运往某销地的运费 ;

列差额 :

第 1 1 1 列 列差额 : 最小运费 1 1 1 , 次最小运费 3 3 3 , 差额是 2 2 2 ;

第 2 2 2 列 列差额 : 最小运费 4 4 4 , 次最小运费 9 9 9 , 差额是 5 5 5 ;

第 3 3 3 列 列差额 : 最小运费 2 2 2 , 次最小运费 3 3 3 , 差额是 1 1 1 ;

第 4 4 4 列 列差额 : 最小运费 5 5 5 , 次最小运费 8 8 8 , 差额是 3 3 3 ;

行差额 :

第 1 1 1 行 行差额 : 最小运费 3 3 3 , 次最小运费 3 3 3 , 差额是 0 0 0 ;

第 2 2 2 行 行差额 : 最小运费 1 1 1 , 次最小运费 2 2 2 , 差额是 1 1 1 ;

第 3 3 3 行 行差额 : 最小运费 4 4 4 , 次最小运费 5 5 5 , 差额是 1 1 1 ;

以 第 1 1 1 列 列差额 为例进行分析 , 最小运费 1 1 1 , 次最小运费 3 3 3 , 差额是 2 2 2 ; 如果不能使用最小运费 1 1 1 , 那么退而求其次 , 使用次最小运费 3 3 3 ; 最优方案无法使用 , 考虑次优方案 , 这两个方案的差距就是 列差额 2 2 2 , 次优方案比最优方案运费高 , 高 2 2 2 ;

第二列的列差额是 5 5 5 , 如果不能使用最优方案 , 使用次优方案 , 每个都要增加运费 5 5 5 , 这个增加的就太多了 , 应该 优先满足差额较高的行列 优先安排运输 ;

" Vogel 方法 " 将全局的最优考虑了进去 , 不再追求局部最优 , 使用该方法得出的初始基可行解 , 距离最优解更近 , 可以迭代更少次数 ;

第 1 1 1 个基变量 :

从所有 没有被划掉 的并且 没有被安排 的的运费中找到差额最大的 , 是 B 2 \rm B_2 B2​ 的列差额 5 5 5 ;

B 2 \rm B_2 B2​ 列最小运费 : 这里优先给 B 2 \rm B_2 B2​ 销地的最小运费 4 4 4 安排运输 , 避免为其安排次小运费 , 对应表格第 3 3 3 行第 2 2 2 列 , A 3 \rm A_3 A3​ 产地运往 B 2 \rm B_2 B2​ 销地的运费 ;

产地分析 : 对于产地 A 3 \rm A_3 A3​ 来说 , 其生产 9 9 9 个 , 已经安排了 0 0 0 个 , 还可以再安排 9 9 9 个 ;

销地分析 : 对于销地 B 2 \rm B_2 B2​ 来说需求 6 6 6 个 , 已经安排了 0 0 0 个 , 还可以再安排 6 6 6 个 ;

最大安排最小运费运输 , 从 A 3 \rm A_3 A3​ 向 B 2 \rm B_2 B2​ 运输 6 6 6 个产品 ;

此时 B 2 \rm B_2 B2​ 的销量已经全部消耗完毕 , 该列就不需要安排其它产地向 B 2 \rm B_2 B2​ 销地运输了 , 可以划掉这一列 , 讨论其它列的运输问题 ;

第 2 2 2 个基变量 :

划掉了 B 2 \rm B_2 B2​ 行 , 这里重新计算行差与列差 ,

B 1 \rm B_1 B1​ , B 3 \rm B_3 B3​ 列最小运费 与 次小运费 没有变化 , 行差额不变 ;

A 1 \rm A_1 A1​ , A 2 \rm A_2 A2​ 行最小运费 与 次小运费 没有变化 , 行差额不变 ;

A 3 \rm A_3 A3​ 行差额需要重新计算 , 最小运费被划掉了 , 此时最小运费是 5 5 5 , 次小运费是 7 7 7 , 行差额变为 2 2 2 ;

从所有 没有被划掉 的并且 没有被安排 的的运费中找到差额最大的 , 是 B 4 \rm B_4 B4​ 的列差额 3 3 3 ;

B 4 \rm B_4 B4​ 列最小运费 : 这里优先给 B 4 \rm B_4 B4​ 销地的最小运费 5 5 5 安排运输 , 避免为其安排次小运费 , 对应表格第 3 3 3 行第 4 4 4 列 , A 3 \rm A_3 A3​ 产地运往 B 4 \rm B_4 B4​ 销地的运费 ;

产地分析 : 对于产地 A 3 \rm A_3 A3​ 来说 , 其生产 9 9 9 个 , 已经安排了 6 6 6 个 , 还可以再安排 3 3 3 个 ;

销地分析 : 对于销地 B 4 \rm B_4 B4​ 来说需求 6 6 6 个 , 已经安排了 0 0 0 个 , 还可以再安排 6 6 6 个 ;

最大安排最小运费运输 , 从 A 3 \rm A_3 A3​ 向 B 4 \rm B_4 B4​ 运输 3 3 3 个产品 ;

此时 A 3 \rm A_3 A3​ 的产量已经全部消耗完毕 , 该行就不需要安排其它销地运输了 , 可以划掉这一行 , 讨论其它列的运输问题 ;

第 3 3 3 个基变量 :

划掉了 B 2 \rm B_2 B2​ 行 , 这里重新计算行差与列差 ,

A 1 \rm A_1 A1​ , A 2 \rm A_2 A2​ 行最小运费 与 次小运费 没有变化 , 行差额不变 ;

B 1 \rm B_1 B1​ , B 3 \rm B_3 B3​ 列最小运费 与 次小运费 没有变化 , 列差额不变 ;

B 4 \rm B_4 B4​ 列差额需要重新计算 , 最小运费被划掉了 , 此时最小运费是 8 8 8 , 次小运费是 10 10 10 , 行差额变为 2 2 2 ;

从所有 没有被划掉 的并且 没有被安排 的的运费中找到差额最大的 , 是 B 1 \rm B_1 B1​ 和 B 4 \rm B_4 B4​ 的列差额 2 2 2 ; 这两个任选一个都可以 ;

B 4 \rm B_4 B4​ 列最小运费 : 这里优先给 B 4 \rm B_4 B4​ 销地的最小运费 8 8 8 安排运输 , 避免为其安排次小运费 , 对应表格第 2 2 2 行第 4 4 4 列 , A 2 \rm A_2 A2​ 产地运往 B 4 \rm B_4 B4​ 销地的运费 ;

产地分析 : 对于产地 A 2 \rm A_2 A2​ 来说 , 其生产 4 4 4 个 , 已经安排了 6 6 6 个 , 还可以再安排 4 4 4 个 ;

销地分析 : 对于销地 B 4 \rm B_4 B4​ 来说需求 6 6 6 个 , 已经安排了 3 3 3 个 , 还可以再安排 3 3 3 个 ;

最大安排最小运费运输 , 从 A 2 \rm A_2 A2​ 向 B 4 \rm B_4 B4​ 运输 3 3 3 个产品 ;

此时 B 4 \rm B_4 B4​ 的销量已经全部消耗完毕 , 该列就不需要安排其它产地向 B 4 \rm B_4 B4​ 销地运输了 , 可以划掉这一列 , 讨论其它列的运输问题 ;

第 4 4 4 个基变量 :

划掉了 B 4 \rm B_4 B4​ 行列 , 这里重新计算行差与列差 ,

A 1 \rm A_1 A1​ , A 2 \rm A_2 A2​ 行最小运费 与 次小运费 没有变化 , 行差额不变 ;

B 1 \rm B_1 B1​ , B 3 \rm B_3 B3​ 列最小运费 与 次小运费 没有变化 , 列差额不变 ;

从所有 没有被划掉 的并且 没有被安排 的的运费中找到差额最大的 , 是 B 1 \rm B_1 B1​ 的列差额 2 2 2 ;

B 1 \rm B_1 B1​ 列最小运费 : 这里优先给 B 1 \rm B_1 B1​ 销地的最小运费 1 1 1 安排运输 , 避免为其安排次小运费 , 对应表格第 2 2 2 行第 1 1 1 列 , A 2 \rm A_2 A2​ 产地运往 B 1 \rm B_1 B1​ 销地的运费 ;

产地分析 : 对于产地 A 2 \rm A_2 A2​ 来说 , 其生产 4 4 4 个 , 已经安排了 3 3 3 个 , 还可以再安排 1 1 1 个 ;

销地分析 : 对于销地 B 1 \rm B_1 B1​ 来说需求 3 3 3 个 , 已经安排了 0 0 0 个 , 还可以再安排 3 3 3 个 ;

最大安排最小运费运输 , 从 A 2 \rm A_2 A2​ 向 B 1 \rm B_1 B1​ 运输 1 1 1 个产品 ;

此时 A 2 \rm A_2 A2​ 的产量已经全部消耗完毕 , 该行就不需要安排其它销地运输了 , 可以划掉这一行 , 讨论其它列的运输问题 ;

第 5 5 5 个基变量 :

划掉了 A 2 \rm A_2 A2​ 行 , 这里重新计算行差与列差 ,

A 1 \rm A_1 A1​ , A 2 \rm A_2 A2​ 行最小运费 与 次小运费 没有变化 , 行差额不变 ;

从所有 没有被划掉 的并且 没有被安排 的的运费中找到差额最大的 , A 1 \rm A_1 A1​ 的行差额 0 0 0 ;

A 1 \rm A_1 A1​ 列最小运费 : 这里优先给 A 1 \rm A_1 A1​ 销地的最小运费 3 3 3 安排运输 , 避免为其安排次小运费 , 对应表格第 1 1 1 行第 1 1 1 列 , A 1 \rm A_1 A1​ 产地运往 B 1 \rm B_1 B1​ 销地的运费 ; ( 次小运费 = 最小运费 , 任选一个即可 )

产地分析 : 对于产地 A 1 \rm A_1 A1​ 来说 , 其生产 7 7 7 个 , 已经安排了 0 0 0 个 , 还可以再安排 7 7 7 个 ;

销地分析 : 对于销地 B 1 \rm B_1 B1​ 来说需求 3 3 3 个 , 已经安排了 1 1 1 个 , 还可以再安排 2 2 2 个 ;

最大安排最小运费运输 , 从 A 1 \rm A_1 A1​ 向 B 1 \rm B_1 B1​ 运输 2 2 2 个产品 ;

此时 B 1 \rm B_1 B1​ 的销量已经全部消耗完毕 , 该列就不需要安排其它产地向 B 1 \rm B_1 B1​ 销地运输了 , 可以划掉这一列 , 讨论其它列的运输问题 ;

第 6 6 6 个基变量 :

此时只剩下最后一个运费没有被安排 , A 1 \rm A_1 A1​ 产地运往 B 3 \rm B_3 B3​ 销地的运费 ;

产地分析 : 对于产地 A 1 \rm A_1 A1​ 来说 , 其生产 7 7 7 个 , 已经安排了 2 2 2 个 , 还可以再安排 5 5 5 个 ;

销地分析 : 对于销地 B 3 \rm B_3 B3​ 来说需求 5 5 5 个 , 已经安排了 0 0 0 个 , 还可以再安排 5 5 5 个 ;

最大安排最小运费运输 , 从 A 1 \rm A_1 A1​ 向 B 3 \rm B_3 B3​ 运输 5 5 5 个产品 ;

此时 B 3 \rm B_3 B3​ 的销量已经全部消耗完毕 , 该列就不需要安排其它产地向 B 3 \rm B_3 B3​ 销地运输了 , 可以划掉这一列 , 讨论其它列的运输问题 ;

至此 , 所有的产量与销量分配完毕 ;

上述初始基可行解方案总运费 :

( 2 × 3 ) + ( 3 × 5 ) + ( 1 × 1 ) + ( 3 × 8 ) + ( 4 × 6 ) + ( 3 × 5 ) = 85 \rm ( 2 \times 3 ) + ( 3 \times 5 ) + ( 1 \times 1 ) + ( 3 \times 8 ) + ( 4 \times 6 ) + ( 3 \times 5 ) = 85 (2×3)+(3×5)+(1×1)+(3×8)+(4×6)+(3×5)=85

最小元素法求出来的初始基可行解的 总运费是 86 86 86 , " Vogel 方法 " 比 " 最小元素法 " 能找出更近的初始基可行解 ;

表上作业法找初始基可行解 , 两种方法 " 最小元素法 " 和 " Vogel 方法 ( 差额法 ) " , 其中 Vogel 方法 得到的初始基可行解更靠近最优解 ;

下面开始判断该 初始基可行解 是否是 最优解 ;

最优解判别 : 得到一组 基可行解 之后 , 使用 检验数 判定该解是否是最优解 ;

检验数符号 : 变量 x i j \rm x_{ij} xij​ 的检验数记作 λ i j \rm \lambda_{ij} λij​ ;

检验数判定原则 : 运输规划的 目标函数求最小值 时 , 所有的 非基变量检验数 λ i j \rm \lambda_{ij} λij​ 都非负 , 该基可行解就是最优解 , 该运输方案是最优方案 ;

求检验数的方法 : ① 闭回路法 , ② 位势法 ;

闭回路法 :

上述示例中找了一个 A 2 \rm A_2 A2​ 到 B 4 \rm B_4 B4​ 的格子对应的非基变量 x 24 \rm x_{24} x24​ 找闭回路 , 实际上任意一个非基变量都存在一个闭回路 ;

此时找到了针对最优解的判定方案 , 是针对 非基变量 进行判断 , 对于 任意一个非基变量 , 都可以找到这样的闭回路 ,

出发的格子中 增加运输量 , 然后某个格子需要 减少运输量 , 增加 与 减少 依次交替 , 最终能回到初始的格子, 达到产销平衡 ;

出发的格子使用加号 + + + , 第二个格子使用减号 − - − , 之后的歌词依次使用 加号减号交替 + − +- +− 符号 ;

让其运费做一个 " + − + − ⋯ +-+-\cdots +−+−⋯ " 运算 , 最终看代数和 ;

如果代数和 大于等于 0 0 0 , 说明当前的非基变量格子取 0 0 0 就是 最优选择 ;

如果代数和 小于 0 0 0 , 说明当前的非基变量格子取 0 0 0 不是最优选择 ;

运输规划问题 :

使用最小元素法求得的初始基可行解 :

使用 最小元素法, 得到初始基可行解 : { x 13 = 4 x 14 = 3 x 21 = 3 x 23 = 1 x 32 = 6 x 34 = 3 \begin{cases} \rm x_{13} = 4 \\\\ \rm x_{14} = 3 \\\\ \rm x_{21} = 3 \\\\ \rm x_{23} = 1 \\\\ \rm x_{32} = 6 \\\\ \rm x_{34} = 3 \end{cases} ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧​x13​=4x14​=3x21​=3x23​=1x32​=6x34​=3​

计算检验数 :

使用闭回路法 , 逐个计算每个非基变量的检验数 ,

以非基变量为起点 , 出发的格子使用加号 + + + , 第二个格子使用减号 − - − , 之后的歌词依次使用 加号减号交替 + − +- +− 符号 ;

计算上述闭回路的运费代数和 ,

如果代数和 大于等于 0 0 0 , 说明当前的非基变量格子取 0 0 0 就是 最优选择 ;

如果代数和 小于 0 0 0 , 说明当前的非基变量格子取 0 0 0 不是最优选择 ;

这里以计算 σ 24 \rm \sigma_{24} σ24​ 检验数为例 :

A 24 + \rm A_{24} + A24​+ , A 23 − \rm A_{23} - A23​− , A 13 + \rm A_{13} + A13​+ , A 14 − \rm A_{14} - A14​−

σ 24 = ( 1 × 8 ) − ( 1 × 2 ) + ( 1 × 3 ) − ( 1 × 10 ) = − 1 \rm \sigma_{24} = ( 1 \times 8 ) - ( 1 \times 2 ) + ( 1 \times 3 ) - ( 1 \times 10 ) = -1 σ24​=(1×8)−(1×2)+(1×3)−(1×10)=−1

检验数小于 0 0 0 ;

计算出的 非基变量 检验数使用 蓝色括号字体 写在表格中 :

上述检验数中 , σ 24 \rm \sigma_{24} σ24​ 为负数 , 需要进行换基 , 该非基变量就是入基变量 ;

该检验数的闭合回路如下 : A 24 + \rm A_{24} + A24​+ , A 23 − \rm A_{23} - A23​− , A 13 + \rm A_{13} + A13​+ , A 14 − \rm A_{14} - A14​− ;

在 − - − 符号的基变量中挑选一个最小的 , 作为出基变量 ;

换基之后的结果如下 :

经过上述计算后的运费表格如下 :

计算当前的总运费 :

( 3 × 5 ) + ( 10 × 2 ) + ( 1 × 3 ) + ( 8 × 1 ) + ( 4 × 6 ) + ( 3 × 5 ) = 85 \rm ( 3 \times 5 ) + ( 10 \times 2 ) + ( 1 \times 3 ) + ( 8 \times 1 ) + ( 4 \times 6 ) + ( 3 \times 5 ) = 85 (3×5)+(10×2)+(1×3)+(8×1)+(4×6)+(3×5)=85

计算检验数验证 , 是最优解 ;

运输规划问题 :

可以使用 " 最小元素法 " 或 " Vogel 方法 " 找初始基可行解 , 这里使用 最小元素法 ;

【运筹学】表上作业法 ( 求初始基可行解 | 最小元素法 ) 博客中有详细的 " 最小元素法 " 的分析过程 , 这里只进行简要分析 ;

基变量个数 是 m + n − 1 = 4 + 3 − 1 = 6 \rm m+ n - 1 = 4 + 3 - 1 = 6 m+n−1=4+3−1=6

最小元素法找初始基可行解:

① x 31 \rm x_{31} x31​ 运费为 1 1 1 最小 , 安排 3 3 3 个 , B 1 \rm B_1 B1​ 销地满足 , 划掉该列 ;

② x 32 \rm x_{32} x32​ 运费为 2 2 2 最小 , 安排 6 6 6 个 , B 2 \rm B_2 B2​ 销地满足 , A 3 \rm A_3 A3​ 产量也满足 , 这里注意除了最后一个基变量之外 , 不能同时删除一行一列 , 每次只能删除一行 , 或者删除一列 ; 这里选择划掉 B 2 \rm B_2 B2​ 销地 这一列 ;

③ x 23 \rm x_{23} x23​ 运费为 3 3 3 最小 , 安排 4 4 4 个 , A 3 \rm A_3 A3​ 产量满足 , 划掉 A 3 \rm A_3 A3​ 行 ;

④ x 13 \rm x_{13} x13​ 运费为 4 4 4 最小 , 安排 1 1 1 个 , B 3 \rm B_3 B3​ 销量满足 , 划掉 B 3 \rm B_3 B3​ 列 ;

⑤ x 14 \rm x_{14} x14​ 运费为 4 4 4 最小 , 安排 6 6 6 个 , A 1 \rm A_1 A1​ 产量满足 , 划掉 A 1 \rm A_1 A1​ 行 ;

⑥ 剩下最后一个变量 x 34 \rm x_{34} x34​ , 安排 0 0 0 个 ; 划掉该行改了 , 所有的运输都安排完毕 ;

使用最小元素法找到的初始基变量与基可行解 :

计算检验数 判定上述 初始基可行解 是否是 最优解 ;

每个非基变量 , 都要计算一次检验数 ;

1. 计算 σ 11 \sigma_{11} σ11​ 检验数

使用 闭回路法 计算检验数 , 首先要确定闭回路 ; 以非基变量为起点 , 然后构造回路 , 只能在基变量对应的格子位置拐弯 ;

σ 11 = 3 − 1 + 6 − 4 = 4 ≥ 0 \sigma_{11} = 3 - 1 + 6 - 4 =4 \geq 0 σ11​=3−1+6−4=4≥0

该检验数 ≥ 0 \geq 0 ≥0 , 如果按照这个回路调整运费会增加 , 每调整一个产品都会增加 4 4 4 个单位运费 ;

计算检验数时 , 只计算拐弯的基变量的运费 , 经过的基变量运费不计算 ;

2. 计算 σ 12 \sigma_{12} σ12​ 检验数

使用 闭回路法 计算检验数 , 首先要确定闭回路 ; 以非基变量为起点 , 然后构造回路 , 只能在基变量对应的格子位置拐弯 ;

σ 12 = 11 − 2 + 6 − 4 = 11 ≥ 0 \sigma_{12} = 11 - 2 + 6 - 4 =11 \geq 0 σ12​=11−2+6−4=11≥0

该检验数 ≥ 0 \geq 0 ≥0 , 如果按照这个回路调整运费会增加 , 每调整一个产品都会增加 11 11 11 个单位运费 ;

计算检验数时 , 只计算拐弯的基变量的运费 , 经过的基变量运费不计算 ;

3. 计算 σ 21 \sigma_{21} σ21​ 检验数

使用 闭回路法 计算检验数 , 首先要确定闭回路 ; 以非基变量为起点 , 然后构造回路 , 只能在基变量对应的格子位置拐弯 ;

σ 21 = 7 − 1 + 6 − 4 + 4 − 3 = 9 ≥ 0 \sigma_{21} = 7 - 1 + 6 - 4 + 4 - 3 =9 \geq 0 σ21​=7−1+6−4+4−3=9≥0

该检验数 ≥ 0 \geq 0 ≥0 , 如果按照这个回路调整运费会增加 , 每调整一个产品都会增加 9 9 9 个单位运费 ;

计算检验数时 , 只计算拐弯的基变量的运费 , 经过的基变量运费不计算 ;

4. 计算 σ 22 \sigma_{22} σ22​ 检验数

使用 闭回路法 计算检验数 , 首先要确定闭回路 ; 以非基变量为起点 , 然后构造回路 , 只能在基变量对应的格子位置拐弯 ;

σ 22 = 7 − 2 + 6 − 4 + 4 − 3 = 8 ≥ 0 \sigma_{22} = 7 - 2 + 6 - 4 + 4 - 3 =8 \geq 0 σ22​=7−2+6−4+4−3=8≥0

该检验数 ≥ 0 \geq 0 ≥0 , 如果按照这个回路调整运费会增加 , 每调整一个产品都会增加 8 8 8 个单位运费 ;

计算检验数时 , 只计算拐弯的基变量的运费 , 经过的基变量运费不计算 ;

5. 计算 σ 24 \sigma_{24} σ24​ 检验数

使用 闭回路法 计算检验数 , 首先要确定闭回路 ; 以非基变量为起点 , 然后构造回路 , 只能在基变量对应的格子位置拐弯 ;

σ 24 = 8 − 4 + 4 − 3 = 5 ≥ 0 \sigma_{24} = 8 - 4 + 4 - 3 =5 \geq 0 σ24​=8−4+4−3=5≥0

该检验数 ≥ 0 \geq 0 ≥0 , 如果按照这个回路调整运费会增加 , 每调整一个产品都会增加 5 5 5 个单位运费 ;

计算检验数时 , 只计算拐弯的基变量的运费 , 经过的基变量运费不计算 ;

6. 计算 σ 33 \sigma_{33} σ33​ 检验数

使用 闭回路法 计算检验数 , 首先要确定闭回路 ; 以非基变量为起点 , 然后构造回路 , 只能在基变量对应的格子位置拐弯 ;

σ 33 = 10 − 6 + 4 − 4 = 4 ≥ 0 \sigma_{33} = 10 - 6 + 4 - 4 =4 \geq 0 σ33​=10−6+4−4=4≥0

该检验数 ≥ 0 \geq 0 ≥0 , 如果按照这个回路调整运费会增加 , 每调整一个产品都会增加 4 4 4 个单位运费 ;

计算检验数时 , 只计算拐弯的基变量的运费 , 经过的基变量运费不计算 ;

经过上述运算 , 所有的非基变量检验数都 ≥ 0 \geq 0 ≥0 , 当前的基可行解就是最优解 ;