[译介]分子轨道和有机化学反应：分子轨道理论

（）挖个新坑（雾

本文全部内容译自Ian Fleming的Molecular Orbitals and Organic Chemical Reactions （Reference Edition)，本人保有由编译工作所带来的、受赛里斯著作权法等法律、法规和政策以及国际上的相关公约、法律等所保护的一切著作权利。

任何人可在学习和研究等等这类非商业用途上自由复制、引用此译本的全体或部分。未经授权不得用于商业用途。您如对该译本有任何意见或建议，欢迎评论区、私信给出更好的建议。

为了理解两个氢原子之间所形成的最简单化学键的本质，我们要观察两个原子靠近到成键距离时对电子分布产生的影响，但首先我们需要氢原子的图象。由于氢原子仅由一个质子和一个电子组成，我们只需要描述该电子的空间分布。其通常表示为波函数(wave function \phi )，其中 \phi^{2}d\tau 是在体积 d\tau 中发现电子的概率， \phi^{2}d\tau 对整个空间的 积分为1。波函数是基于数学的描述，并且可正可负；它可表示为包含实部和虚部的复数，但在本书的任何讨论中都不需要用到它。其仅当平方时才具有现实的物理意义——即在给定的空间内发现电子的概率。量子理论[1]提供了一系列可行的波动方程，但但在此只有能量最低的波函数起作用，其中电子的分布被描述为处于1s轨道中。轨道绕核呈球形对称分布，在中心达到最大值，并迅速减小，因此在半径为1.4Å的球体内找到电子的概率为90%，在2Å半径的范围内找到电子的概率超过99%。据计算，该轨道的能量比完全分离的电子和质子的能量低13.60eV。

我们需要图象来说明电子分布，最常见的是简单画一个圆，如图1.1a所示，该圆可以被认为是球形等值面的一个截面，其中电子有90%的概率被发现。本图足以满足我们在这本书中所需要讨论的大部分内容，但我们应当看看其他的图象，因为仅一个圆圈本身掩盖了一些值得鉴别的特征。因此，图1.1b中更详尽的显示了更多等值线的截面。另一幅图则是将电子分布描述为云所形成的截面，这不太轻易的快速画出来，如图1.1c，人们想象自己眨了许多次眼睛,并记录下每次眨眼时电子所在的位置。该图为我们常用说法提供了依据，在这种说法中，给定体积内电子布居被称为电子密度。

通过其球状对称的特点，我们还可以将半径 r 处的电子分布同 r 的关系绘制出来，如图1.2a所示，表明电子分布随着半径增大迅速减小。图示中1.2Å的范德华半径不具备理论意义—它只是根据固体结构得出的经验半径，即相邻分子中两个C-H键的氢原子间距离的一半。[2]它并无一个固定值，而是多个测量值的平均值。考察其径向电子密度是另一种理解电子分布的办法，我们表示出在一个半径为 r 的球同 r+dr 的球之间发现电子的概率。在此呈现了该关系，如图1.2b所示，从核出发，半径到0.529Å时发现电子的概率达到最大值，该图表明，尽管波函数在核处为最大值，但在那里恰好找到电子的概率却很小。0.529Å的距离与早期氢原子行星模型中计算得出的电子轨道半径相近。它被称作波尔半径 a_{0} ，在分子轨道计算中常用作长度单位。

为了理解氢分子的成键，我们应当观察当两个氢原子足够近直到它们的原子轨道能够发生相互作用时会产生什么。我们现在有两个质子和两个原子核，即便是这么小的一个分子，我们也不能指望理论能向我们给出完整的结论。我们需要对整个分子，即分子轨道上的电子分布进行描述。解决该问题的办法是采纳第一个近似：两个原子或多或少保持不变，这样分子的描述将近似于两个孤立原子的和。因此，我们将两个原子轨道以线性组合的方式结合在方程1.1中，其中描述新的电子分布的函数——分子轨道称为 \sigma ， \phi_{1} 和 \phi_{2} 是原子1和2的1s轨道的波函数。 σ=c_{1}\phi_{1}+c_{2}\phi_{2} \tag{1.1}

系数 c_{1} 和 c_{2} 是原子轨道对分子轨道贡献的度量。在这种情境下，两个原子是相同的，因而它们的大小显然相等，但它们可以是正的，或是负的。为了得到电子的分布，我们将方程1.1中的函数平方，在方程1.2中有两种表示方法。

σ^{2}=(c_{1}\phi_{1}+c_{2}\phi_{2})^{2}=(c_{1}\phi_{1})^{2}+(c_{2}\phi_{2})^{2}+2c_{1}\phi_{1}c_{2}\phi_{2}\tag{1.2}

将式子展开后，我们会注意到分子轨道 \sigma^{2} 经由项 2c_{1}\phi_{1}c_{2}\phi_{2} ，从而形成异于两个原子轨道的累加产生的结果，即 (c_{1}\phi_{1})^{2}+(c_{2}\phi_{2})^{2} 。所以我们能得到两个解（图1.3）。在第一个解中， c_{1} 和 c_{2} 均为正值，相同符号的轨道相互靠近放置；两原子间的电子密度增加（即阴影区域），因此这些电子所携带的负电荷吸引两个带正电荷的原子核。这引起了能量的降低，如图1.3所示，在图中，这个轨道旁边的水平线被放置在较低的位置。在轨道结合的第二个解中，c_{1} 和 c_{2} 的符号是相反的，如果这个轨道中有电子，在原子核之间的空间将会存在较低的电子密度，因为函数改变了符号。我们通过给其中一个轨道涂上阴影来表示符号的变化，我们称在符号变化处将函数平分的平面为一个节点（node）。如果这个轨道上有电子，原子核之间电子密度的减少会导致它们之间产生排斥力；因此，如果我们想在这个轨道上有电子，并且仍使原子核间保持尽可能近的距离，就必须向这个体系中输入能量。总之，通过两个氢原子之间的结合，我们创造了两个新的轨道， σ 和 σ^{*} ，我们称之为分子轨道；前者成键，后者反键（星号常以表示反键轨道）。在分子处于基态时，两个电子将在标记为的轨道上。因而当我们成键时，能量降低值等于图1.3中 E_{σ} 值的两倍（因为在成键轨道中有两个电子,故能量降低两倍）。

将两原子结合在一起的力的大小显然取决于成键轨道的重叠程度。如果我们将两个1s轨道从3Å这样一个基本没有重叠的距离，通过成键组合的方式形成重叠，重叠的范围会逐渐增加。重叠的数学描述是一个积分 S_{12} （方程1.3），称为重叠积分(overlap integral)，对于一对1s轨道，无限分离时其值为0，并在升为1在达到完全重叠（图1.4）。

S_{12}=\int\phi_{1}\phi_{2}d\tau\tag{1.3}

重叠对电子能量造成的影响的数学描述是复杂的，但我们应当了解一些术语，这些术语将在本书的其他地方时不时地进行使用。成键分子轨道中电子的能量值E由式1.4给出，而反键分子轨道的能量值E由式1.5给出:

E=\frac{\alpha+\beta}{1+S}\tag{1.4}

E=\frac{\alpha-\beta}{1-S}\tag{1.5}

其中符号 \alpha 表示孤立的原子轨道中所含电子的能量，被称为库仑积分(Coulomb integral) 。符号 \beta 所代表的函数表示一个电子由于同时处于两个原子核的场，而产生的对能量的贡献，称为共振积分(resonance integral)[3] 。它与S大致成正比，所以重叠积分在方程中出现了两次。我们应当认识到，使用“共振”这个词并不意味着振动，它与价键理论中的“共振”也并非完全相同。在这两种情况下使用该词是因为其函数的数学形式与振荡器的机械耦合相似。我们也用“离域化”(delocalised)和“离域”(delocalisation)来描述蕴含于\beta函数中的电子分布——与“共振”不同，这些词没有误导性，是更合适用来描述的词。

函数 \beta 为负数，使得方程1.4中E的值降低，方程1.5中E的值升高。在本书中，在使用\beta时，在图表上不会给出其标识，因为这个标识可能会产生误导。符号\beta应解释为|\beta|，即\beta的正绝对值。由于图表总向上绘制更高能量的轨道，且常常标出\alpha值，所以显而易见，\beta值描述的是低于\alpha值的而下降的能量，以及高于 \alpha 值的而升高的能量。

重叠对氢分子产生的相异于分立的两个氢原子而言的影响，作为关于核间距的函数，如图1.5所示。若成键轨道被填满(图1.5a)，则由电子产生的对能量降低的贡献(方程1.4)随着两个氢原子距离从无限大到彼此相互靠近而稳步下降(曲线A)。与此同时，原子核彼此间的排斥越来越强，原子核对能量升高的贡献稳步上升(曲线B)。这两者的总和便是我们熟悉的Morse曲线(曲线C)，表明核间距和能量之间的关系，且在键长处能量最低。如果我们填满反键轨道(图1.5b)，曲线B不会发生变化。电子的能量则将由方程1.5描述，它只在分立的原子核间产生了一点屏蔽，曲线A在最初时表现为一条值(变动)微小的曲线，即便如此，也会先于Morse曲线形成排斥。合成曲线C则描述了原子核靠近时能量的稳定增加。成键轨道的特点是原子核被键合在一起，而反键轨道的特点是如果要填满其轨道，必须要能够先填占能形成足够补偿的成键轨道，否则原子间会发生解离。如果两个轨道都被占满，那么总的来说是形成反键，并且不可能对已填满的反键轨道再形成任何补偿。

从公式1.4和1.5的形式可以看出，\alpha项与图1.3中记做 1s_{H} 的孤立原子的能级有关，而\beta项与标记为 E_{\sigma} (和标记为 E_{\sigma*} )的能量下降(上升)有关。式1.4和1.5表明，由于成键轨道线性组合的分母是 1+S ，而反键轨道线性组合的分母是 1-S ，因此成键轨道能量降低的幅度没有反键轨道能量升高的幅度大。此外，将两个电子填入成键轨道并不能达到将一个电子放入轨道产生的能量降低的两倍的效果。如果两个电子自旋方向相反，我们可以将其放入同一轨道，但它们仍旧相互排斥，因为它们必须共享同一空间；因此，在使第二个电子进入 \sigma 轨道的过程中，我们失去了一些本可得到的成键(效应)。综上，图1.3中E_{\sigma}的值小于E_{\sigma*}的值。这就是为何两个氦原子不能结合形成\ce{He_{2}}分子的原因。两个氦原子中有四个电子，其中两个进入 \ce{He_{2}} 分子的\sigma-成键轨道，两个进入\sigma*-反键轨道。由于 2E_{\sigma} 大于 2E_{\sigma*} ，我们需要额外的能量来保持两个氦原子结合在一起。

在同一轨道上的两个电子相互避开，一个电子在轨道的一侧，而另一个电子在大多数情况下在轨道的另一侧，所以在轨道上填入第二个电子产生的能量损失不是很大。这种电子运动的同步性被称为电子相关(electron correlation)。根据式1.4和1.5，一个电子对另一个电子的排斥所引起的能量提升效应自动包括在计算中，但每个电子被视作相对于另一个电子具有平均的电荷分布。电子相关效应产生的影响通常不包括在内，对精度的损失不大，但当其包括在内时，计算被描述为组态相互作用(configuration interaction)，在准确的计算中，有时需要进行一些微调。

\alpha和\beta的准确形式表现其数学上的复杂性。它们来自于Schrödinger方程，是对整个坐标的积分，此处用dt表示，以方程1.6和1.7的形式呈现:

\alpha =\int \phi_{1}H\phi_{1}d\tau \tag{1.6}

\beta =\int \phi_{1}H\phi_{2}d\tau \tag{1.7}

H是能量算符，即哈密顿量(Hamiltonian)。即便没有更详尽的阐述，但其显然的说明了项同原子的关系，和 项同原子间相互作用的关系。

同原子轨道一样，我们需要图像来说明分子轨道中的电子分布。在大多数情况下，图1.3中成键和反键轨道的传统描述的图像已经足够清晰——我们对其所描述的东西在认识上有所保留。为了确保我们的确了解到了足够的详细情况，我们可以观察穿过两个原子的

一个截面来表现其等值线(图1.6)。我们看到在成键轨道上靠近原子核的电子云被拉到原子核间的中点(图1.6a)，但在更远的四周，等值线呈现为椭圆形的包络线，并以原子核作为焦点。不同的是，反键轨道在原子核间仍有一些密集的等值线，但更靠外侧的电子云则被推到两个原子核的背侧。节点在原子核间的中点，波函数符号的变化用在一侧阴影的等值线表示。如果这个轨道中有电子，它们在外围的分布将使得原子核分离——原子靠得越近，电子受到排斥向外围的越多，这就解释了为何图1.5b中曲线A能量上升。

我们可以忽略波函数中的符号变化，并沿着核间轴绘制 \sigma^{2} 的曲线，如图1.7所示。实线表示分子轨道，虚线相对用地表示未受扰动的原子轨道\phi^{2}。成键轨道上的电子密度(图1.7a)相对于原子轨道的平方和可以看到存在轻微的收缩，而原子核间的电子密度相对于原子轨道的组合则有所增大，正如我们在考虑方程1.2时所看到的那样。在反键轨道中(图1.7b)则相反，如果该分子轨道中填有电子，则其电子布居相对于原子轨道的平方和会略微增大，原子核之间的电子布居会相应地减少。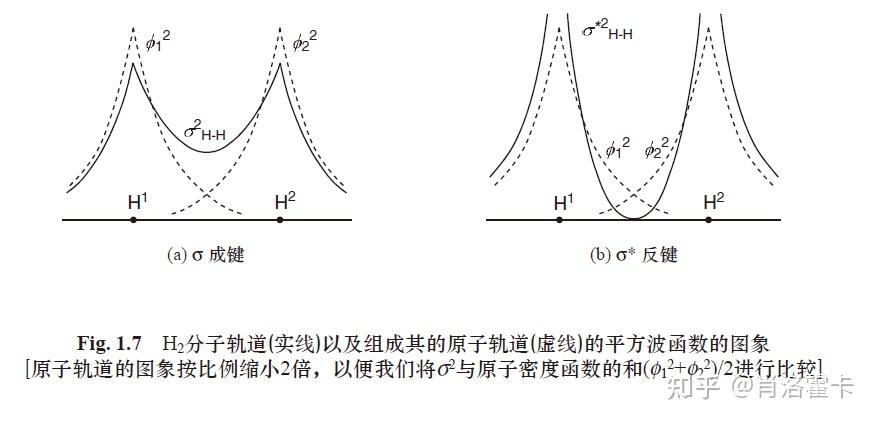

让我们回到方程1.1的系数 c_{1} 和 c_{2} ，它们是每个分子轨道中对每个原子轨道对其贡献的量度(在这种情况下两者相等)。当轨道中有电子时，c值的平方则是对该原子附近电子密度的一种度量。因为在一种自旋状态下，一个轨道中只能有一个该自旋态的电子，因此在每个轨道中，所有c值的平方和必须等于1。由于像 \ce{H2} 这样的同核双原子分子中|c_{1}|必须等于|c_{2}|，我们已经明确了成键轨道中c_{1}和c_{2}的值必须为1/√2=0.707：

如果所有的分子轨道都被填满，那么每个原子的在每个自旋态下都有一个电子，这就给出了对于c值的另一标准，即所有分子轨道中任意的同一原子的全部c值的平方和也必须等于1。因此，氢的 \sigma* -反键轨道的c值将为0.707和-0.707，因为这些值所构成的这个体系符合这两个标准。当然，我们也可以将反键轨道中的c_{1}和c_{2}反过来，使c_{1}是负值，c_{2}为正值。

对系数的推导并不是严格精确的——恰当的归一化涉及重叠积分S，其在成键轨道和反键轨道中以相反的符号出现(参见等式1.4和1.5)。结果是反键轨道上的系数实际上比成键轨道上的系数略大一些。我们不需要在本书所运用的分子轨道理论的水平上进行练习这样的微妙差异，并且它在Hückel理论中根本不是问题，这(Hückel理论)也是我们将应用于 \pi 体系的理论。然而，当我们注意到它是另一种解释反键轨道(图1.3中的 E_{\sigma*} )的反键程度大于成键轨道( E_{\sigma} )的成键程度的方法时，我们将会认识到其重要性。

我们可能好奇，我们是否能引入两个以上的氢原子并使他们结合在一起。我们将首先考虑 三个原子以三角形排列组合在一起的可能性。这首次向我们提出了如何解释三个原子相互 成键的问题。由于有三个原子轨道需要结合，我们不能再像图1.3中那样简单地画出一个 相互作用图，其中只有两个原子轨道。一种解决这个问题的方法是首先将把两个氢原子进 行组合。在此情况下，我们取其中两个氢原子，让它们相互作用形成一个氢分子，然后我 们把图1.8右侧的\sigma和\sigma*轨道与左侧的第三个氢原子的1s轨道组合起来。

目前我们有一个重要的规则：我们只允许组合那些具有相同对称性的轨道，其对称性是相对于所有存在于产物结构中以及我们组合组分的轨道中对称元素而言的。这个问题并非是在两个相同氢原子间形成化学键过程中产生的，因为它们本质上有相同的对称性，但现在我们要将不同性质轨道组合在一起。随着分子变得越来越复杂，对轨道匹配和保持对称性的需求将不断地被重申. 第一个目标是辨认对称元素，并据此对轨道进行分类。因为所有的轨道都是\sigma轨道，所以在本页的平面上有一个很寻常的对称平面，我们将在本书中把它记作xz平面。在这种情况下我们可以忽略它，以及其他类似的对称元素。唯一不寻常的对称元素是我们称为yz平面的面，它从页面的上面延申至下方，并垂直于页面。s轨道和1s轨道对于这个平面来说是对称的，但\sigma*轨道则是反对称的，因为组成他的原子轨道是异相的。因此，我们把这几个轨道标为S(对称 symmetric)或A(反对称 antisymmetric)。

\sigma轨道和1s轨道都是S轨道，它们可以像我们在图1.3中看到的那样相互作用，以创建一对新的标记为 \sigma_{1} 和 \sigma_{2}* 的分子轨道。前者的能量降低了，因为所有的s轨道具有相同的符号，而后者的能量提高了，因为上方的氢原子和下方的两个氢原子之间存在一个节点。后者轨道总体上是反键的，因为氢原子之间存在两度的反键作用，却只有一种成键作用。巧的是，它的能量与\sigma*轨道的能量相同，但我们现在还不能完全证明这一点。无论怎样， \ce{H_{3}} 分子中另一个轨道\sigma*保持不变，因为没有具有与之相应对称性的轨道同它相互作用。

因而我们有三个分子轨道，正如我们有三个原子轨道一样。现在，我们是否有一个稳定的“分子”取决于我们有多少电子。如果我们有两个电子在 \ce{H_{3}^{+}} 中，换句话说，一个被质子化的氢分子，两个电子都会进入\sigma_{1}轨道，而且分子的电子能量会比孤立的质子和 \ce{H_{2}} 分子低。如果我们结合三个氢原子得到具有三个电子的 \ce{H_{3}} ，我们也会得到一个稳定的“分子”，在 \sigma_{1} 中有两个电子，在 \sigma_{2}* 中只有一个电子，这使得总的组合更倾向于成键而非反键。只有在有4个电子的 \ce{H_{3}^{-}} 中，相互作用总体结果呈反键，因为能量升高的相互作用通常大于能量降低的相互作用。这种建立轨道，然后向轨道中填充电子的方法被称为构造方法（aufbau method）。

我们可以以直线方式将三个原子排列并进行组合，即把图1.8中两个较低的氢原子提上来，使它们分别置于上方原子的两侧。由于对称性没有改变，结果将是相似的(图1.9)。 \sigma _{1} 和\sigma _{2}*的成键效应会降低，两个较低氢原子间的重叠会消失。 \sigma* 轨道的反键性质也会减弱，因此它会恢复到和两个相对独立的 1s 轨道相同的能量。

四个氢原子可能的排列方式有很多，但我们仅讨论四面体，因为我们将会用到这些轨道。这一次如图1.3所示，我们将它们成对的组合，先构造两个氢分子，然后考虑当两个氢分子保持在成键距离内，其中一个分子同另一分子互相构成直角时，能量会发生何种变化。

我们可以让一对氢原子沿着x轴对齐，置于图1.10中的右侧，另一对氢原子沿着y轴对齐，在图1.10中的左侧。表现出的对称元素是xz和yz平面。右侧的成键轨道 \sigma_{x} 相对于两个平面都是对称的，记为SS。反键轨道 \sigma_{x}* 相对于xz平面是对称的，但相对于yz平面是反对称的，因此标记为SA。左侧的成键轨道 \sigma _{y} 相对于两个平面都是对称的，也标记为SS。反键轨道 \sigma_{y}* 相对于xz平面反对称，但相对于yz平面是对称的，记作AS。因此，唯一具有相同对称性的轨道是两个成键轨道，它们可以相互作用形成成键组合 \sigma_{1} 和反键组合 \sigma_{2}* 。巧的是，后者同未再次发生改变的轨道 \sigma _{x}* 和 \sigma_{y}* 的能量相同。这并不难理解:在新轨道 \sigma_{1} 和 \sigma_{2}* 中，系数c(忽略完全的归一化处理)为0.5，而非0.707，以便使它们的平方和为1。在反键轨道组合 \sigma_{2}* 中，氢原子间有两重成键关系，四重反键关系，与 \sigma _{x}* 和 \sigma_{y}* 轨道上各一个反键相比，有两重净的反键组合。然而， \sigma_{2}* 轨道的反键存在于系数为 \frac{1}{\sqrt{4}} 的 s 轨道之间，这两重相互作用与系数为 \frac{1}{\sqrt{2}} 的轨道之间的相互作用是相同的(见公式1.3，请务必注意，电子能量的变化粗略的同重叠积分 S 成正比)。

我们现在有四个分子轨道， \sigma_{1} ， \sigma_{2}* ， \sigma _{x}* 和 \sigma_{y}* ，相对于一对氢分子的轨道，一个能量降低，一个能量升高。如果体系中有四个电子，就像两个充满的轨道结合在一起通常出现的情况一样。净结果是相互排斥，因此，两个 \ce{H_{2}} 分子无法结合形成 \ce{H_{4}} 分子。这是一条关键的结论，无论我们在线性组合中使用何种几何角度，都是正确的。这很重要，因为它在最简单的情况下向我们说明了为什么分子存在，为什么它们在极大程度上保持了它们的独立特性——当两个分子接近彼此时，分子轨道间相互作用通常会导致上述这种排斥。克服排斥是化学反应的先决条件，其所需的能量占活化能的主要部分。

碳有s和p轨道，但我们可立即忽略1s对成键的贡献，由于该轨道中的两个电子被核束缚过紧，该轨道不具备产生明显重叠的可能性——电子仅仅屏蔽了原子核，有效的降低了其正电荷。我们余下2s和2p中四个电子用于成键。2s轨道和1s轨道一样是球对称的，但是他有一个球节点，波函数如图1.11a所示，等值面截面图如图1.11b所示，这个节点靠近核，并且成键时同内部球状轨道的重叠往往不重要，使得2s轨道显著的类似于同1s轨道，因此，一个2s轨道往往简单的画作一个圆，如图1.11c所示。氢的1s和碳2s轨道外侧部分的重叠积分S同图1.4所示的两个1s轨道的重叠积分具备类似的形式（区别在于他并不增大到同样高的值，在原子分离程度较大时达到最值，并且在原子重叠时不会趋于1）。碳上2s轨道的能量为-19.5eV，比氢原子的1s轨道能量低5.9eV。由于原子核有6个质子，即使他被核与电子间更长的平均距离以及其他电子的屏蔽所抵消，仍对2s电子的吸引力更大。Slate规则认为两个1s电子中每个电子抵消核电荷中0.85个单位的核电荷，其他2s和2p电子抵消了3×3.5个核电荷，得出核的有效电荷值3.25。

碳上的2p轨道同样各有一个节点，但他们具有完全不同的形状。轨道互相正交，分别沿x, y, z三个方向延申， 2p_{x} 轨道沿x轴所绘制的波函数图象在1.12a中示出，沿轨道截面的等值线轮廓图如1.12b所示。依据这些函数所定义的形状来绘制p轨道几何图形的比例，会使得一切对其成键贡献分析变得无法清晰说明，在此情况下，如图1.12c所示，常会绘出更窄的波瓣，我们对其真实物理图象有所保留。2p轨道的能量为-10.7eV，高于2s轨道，因为其轨道平均离核更远。将三个p轨道—— p_{x} , p_{y} 和 p_{z} 的波函数平方并相加时，整体的电子概率具有球对称性，就像相应的s轨道一样，但集中在离核更远处。

碳形成的化学键是通过s轨道相互重叠形成的，就像在氢分子中一样，s轨道和p轨道重叠，p轨道相互重叠。p轨道和s或p轨道之间的重叠积分 S 取决于它们相互靠近的角度。氢的s轨道沿轴靠近与其在一端上波相相同的p轨道的重叠积分(图1.13)，形成s轨道，随着轨道开始重叠(D)，在离核距离略大于0.9Å时达到最值(C)，s轨道同波相相反的p轨道产生重叠后快速下降(B)，当s轨道中心与碳原子中心重合时(A)变为零。在最后一种组合中，与同相波瓣重叠(无阴影的波瓣通常用来表示波函数中的正)的键合会被同波函数中异相波瓣(阴影)的重叠完全抵消。当然，因为原子核不可能重合，至少在化学领域这种组合是永远无法企及的。两个p轨道以同相的成键方式头碰头靠近时的重叠积分(图1.13b)在原子核相互(G)时开始增大，在核间距为1.5Å(F)时达到最大值，在两者前端波瓣重叠同前端波瓣和后端波瓣重叠相互抵消时(E)降为0，并且最终在完全叠加时降为-1。单个s和p原子轨道波函数的符号(正负号)有时会显得混乱，因而我们采用有阴影和无阴影的标记方法。除了图1.17和图1.18之外，本书中不会使用这些符号，在图1.17和图1.18中，这样的符号表示(的线性组合)是更有效的。

在s和p重叠，p和p重叠这两种情况下，重叠不一定是完全正对着的，但仍旧能对成键有贡献。对于并非完全对齐的轨道，其积分难免有所减小，因为分布在原子核间，起到将原子核结合在一起作用的电子，其布居相应地更少；此外，由于其重叠区域也会偏离核间的中心，原子核相互间屏蔽变得更小。实际上，氢原子上1s轨道和碳上2p轨道的重叠积分与其接近角度 \theta 的余弦值成比例，其中 \theta 为0°对应着从p轨道头部正对靠近， \theta 为90°对应着氢原子从p轨道节面靠近。

在甲烷中包含八个价电子，其中四个来自碳原子，四个来自氢原子，相应的构成了四个分子轨道。我们可以从将两个氢分子组合为 \ce{H_{4}} 复合单元开始，在将该其轨道同碳的原子轨道进行组合。这两者会互相排斥，它们之间所达到最远的距离是四面体的排列方式。在这种排列方式下，正如我们将会遇见到的那样，他们之间仍可保留在所有四个轨道中氢原子，碳原子间的成键相互作用，并且通过这种排列形式实现最大的总成键效应。

我们首先根据两个对称元素：xz平面和yz平面，对轨道进行分类。图1.10中 \ce{H_4} "分子"的分子轨道对称性现置于图1.14的左侧，因为四个氢原子现在相互之间比我们在图1.10中想象的距离更远，故每个轨道的能量都接近氢原子一个孤立1s轨道的能量。单个碳原子的s轨道和p轨道则置于右侧。两侧侧各有两个SS对称性的轨道，但碳的2s轨道与 \sigma_{2}* 轨道相互作用的重叠积分为零——与下方波瓣成键的与上方波瓣所成反键的强度相同。这种相互作用是无效的。因此产生四组相互作用，形成了四个成键分子轨道(如图1.14所示)和四个反键轨道(未在图中示出)。因为其中一个轨道使用碳上2s轨道进行重叠，而2s轨道能量低于2p轨道，该轨道的能量比另三个低。就像两边对应组分的轨道一样，其他三个轨道的能量是完全相同的，这四个轨道是我们需要容纳八个价电子的全部轨道。一定存在一组能量更高的对应反键轨道，但我们现在无需考虑。

在该图中，将碳同任一氢原子结合起来的力都由不止一个分子轨道贡献。对于图1.14中在碳原子下方的两个氢原子而言，其成键由所有s轨道重叠组成的能量最低轨道贡献，此外，成键还包括置于左上和右上，由氢原子1s轨道与碳的2pz轨道和2px轨道重叠构成的轨道的贡献。这两个氢原子在2py轨道的节点上，上面这行中间的分子轨道对其成键没有贡献。然而，画在碳原子上方的氢原子，分别在纸面的前面和后面，它们是通过自己的1s轨道和碳原子的2s, 2py和2pz轨道的重叠而成键的，而非2px轨道。

图1.14使用了原子轨道的经典表示，展示了原子轨道对每个分子轨道的贡献，但它们没有给出产生的电子分布的准确图像。我们可以在Jorgensen和Salem的开创性著作The Organic Chemist`s Book of Orbitals中可以找到更好的图像，本书也可参考其光碟。同样还有些计算机程序可方便大家更轻松地绘制出更真实的图像。图1.15的图片来自Jaguar程序，显示了甲烷的四个满占轨道。以网状线显示分子轨道波函数的其中一个轮廓，符号以阴影的深浅表示。我们很容易看出参与组成的s轨道和p轨道，作为比较，四个轨道在此处排列方式与图1.14相同。