数学建模

2024-06-02 03:35| 来源: 网络整理| 查看: 265

多元统计分析例题及程序主成分分析简述基本思想计算步骤例题程序程序理解因子分析相关性分析回归分析一元回归例题聚类分析

主成分分析简述主成分分析（Principal Component Analysis，PCA），是一种数学降维的统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量，转换后的这组变量叫主成分。在用统计分析方法研究多变量的课题时，变量个数太多就会增加课题的复杂性。人们自然希望变量个数较少而得到的信息较多。主成分分析作为基础的数学分析方法，其实际应用十分广泛，比如人口统计学、数量地理学、分子动力学模拟、数学建模、数理分析等学科中均有应用，是一种常用的多变量分析方法。基本思想主成分分析是设法将原来众多具有一定相关性（比如P个指标），重新组合成一组新的互相无关的综合指标来代替原来的指标。主成分分析，是考察多个变量间相关性一种多元统计方法，研究如何通过少数几个主成分来揭示多个变量间的内部结构，即从原始变量中导出少数几个主成分，使它们尽可能多地保留原始变量的信息，且彼此间互不相关.通常数学上的处理就是将原来P个指标作线性组合，将其线性组合作为新的综合指标。达到降维的目的。计算步骤原始数据标准化计算相关系数矩阵计算特征向量和特征值选取主成分计算综合得分

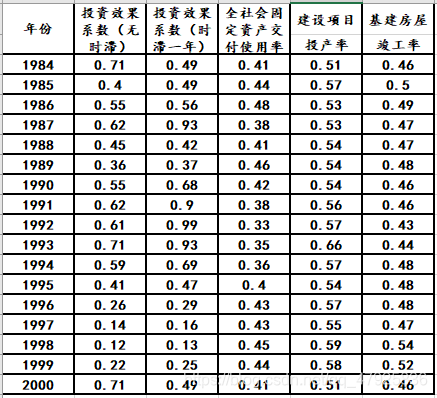
原始数据的标准化

采集m维随机向量 x = （ x 1 , x 2 , ⋯ , x m ） T x=（x_{1},x_{2},\cdots,x_{m}）^{T} x=（x1,x2,⋯,xm）T抽取n个样品 x i = （ x i 1 , x i 2 , ⋯ , x i m ） T , i = 1 , 2 , . . . , n x_{i}=（x_{i1},x_{i2},\cdots,x_{im}）^{T},i=1,2,...,n xi=（xi1,xi2,⋯,xim）T,i=1,2,...,n。且有 n > p n>p n>p构造样本数据矩阵 x = ( x 11 x 12 ⋯ x 1 m x 21 x 22 ⋯ x 2 m ⋮ ⋮ ⋮ ⋮ x n 1 x n 2 ⋯ x n m ) x=\begin{pmatrix} x_{11} &x_{12} &\cdots &x_{1m} \\ x_{21} &x_{22} &\cdots &x_{2m} \\ \vdots &\vdots &\vdots &\vdots \\ x_{n1} &x_{n2} &\cdots &x_{nm} \end{pmatrix} x=⎝⎜⎜⎜⎛x11x21⋮xn1x12x22⋮xn2⋯⋯⋮⋯x1mx2m⋮xnm⎠⎟⎟⎟⎞标准化变换： x i j ′ = x i j − x j ˉ s j x_{ij}'=\frac{x_{ij}-\bar{x_{j}}}{s_{j}} xij′=sjxij−xjˉ其中， x j ˉ = 1 n ∑ i = 1 n x i j , s j 2 = 1 n − 1 ∑ i = 1 n ( x i j − x j ˉ ) 2 \bar{x_{j}}=\frac{1}{n}\sum \limits _{i=1}^{n}x_{ij},\quad s_{j}^{2}=\frac{1}{n-1}\sum\limits _{i=1}^{n}(x_{ij}-\bar{x_{j}})^{2} xjˉ=n1i=1∑nxij,sj2=n−11i=1∑n(xij−xjˉ)2。

计算相关系数矩阵R R = ( r 11 r 12 ⋯ r 1 m r 21 r 22 ⋯ r 2 m ⋮ ⋮ ⋮ ⋮ r n 1 r n 2 ⋯ r n m ) R=\begin{pmatrix} r_{11} &r_{12} &\cdots &r_{1m} \\ r_{21} &r_{22} &\cdots &r_{2m} \\ \vdots &\vdots &\vdots &\vdots \\ r_{n1} &r_{n2} &\cdots &r_{nm} \end{pmatrix} R=⎝⎜⎜⎜⎛r11r21⋮rn1r12r22⋮rn2⋯⋯⋮⋯r1mr2m⋮rnm⎠⎟⎟⎟⎞ 其中， r i j = 1 n − 1 ∑ k = 1 n x k i x k j , n > 1 , i , j = 1 , 2 , ⋯ , m r_{ij}=\frac{1}{n-1}\sum\limits _{k=1}^{n}x_{ki}x_{kj},\quad n>1,\quad i,j=1,2,\cdots,m rij=n−11k=1∑nxkixkj,n>1,i,j=1,2,⋯,m

特征向量和特征值

解特征方程 ∣ λ I − R ∣ = 0 |\lambda I-R|=0 ∣λI−R∣=0可得特征值 λ 1 ⩾ λ 2 ⩾ ⋯ λ m ⩾ 0 \lambda _{1}\geqslant \lambda _{2}\geqslant \cdots \lambda _{m}\geqslant 0 λ1⩾λ2⩾⋯λm⩾0以及对应的特征向量 u 1 , u 2 , ⋯ , u m , u_{1},u_{2},\cdots,u_{m}, u1,u2,⋯,um,其中 u j = ( u 1 j , u 2 j , ⋯ , u m j ) T u_{j}=(u_{1j},u_{2j},\cdots,u_{mj})^{T} uj=(u1j,u2j,⋯,umj)T且 ∥ u j ∥ = 1 , j = 1 , 2 , ⋯ , m \|u_{j}\|=1,j=1,2,\cdots,m ∥uj∥=1,j=1,2,⋯,m则第 j j j个主成分为 y j = u 1 j x 1 + u 2 j x 2 + ⋯ + u m j x m , y_{j}=u_{1j}x_{1}+u_{2j}x_{2}+\cdots+u_{mj}x_{m}, yj=u1jx1+u2jx2+⋯+umjxm,其中， x j = ( x 1 j , x 2 j , ⋯ , x m j ) T , j = 1 , 2 , ⋯ , m x_{j}=(x_{1j},x_{2j},\cdots,x_{mj})^{T},j=1,2,\cdots ,m xj=(x1j,x2j,⋯,xmj)T,j=1,2,⋯,m

对特征值和特征向量的求解，可以列一个直观的表格。

选取主成分

第 j j j个成分的贡献率为 β j = λ j ∑ k = 1 m λ k ( j = 1 , 2 , ⋯ m ) \beta_{j}=\frac{\lambda _{j}}{\sum \limits _{k=1}^{m}\lambda _{k}}\quad \left ( j=1,2,\cdots m \right ) βj=k=1∑mλkλj(j=1,2,⋯m)前 p p p个成分的累计贡献率为 α p = ∑ k = 1 p λ k ∑ k = 1 m λ k \alpha_{p}=\frac{\sum \limits _{k=1}^{p}\lambda _{k}}{\sum \limits _{k=1}^{m}\lambda _{k}} αp=k=1∑mλkk=1∑pλk各成分的方差是递减的，包含的信息也是递减的。实践中一般选取 α p ⩾ 85 % \alpha_{p}\geqslant85\% αp⩾85%

计算综合得分Z Z = ∑ j = 1 p β j y j Z=\sum \limits _{j=1}^{p}\beta _{j}y_{j} Z=j=1∑pβjyj

例题

下表是我国1984-2000年宏观投资的一些数据,试利用主成分分析对投资效益进行分析和排序在这里插入图片描述

程序 data=xlsread('data.xlsx'); %导入数据 X=zscore(data); %标准化数据 R=corrcoef(X); %求相关系数矩阵 [vec,lamba,rate]=pcacov(R); %主成分分析,vec为R特征向量,lamba为R特征值,rate为各个主成分贡献率 vec=vec./sign(sum(vec)) %使特征向量和为正 contr=cumsum(rate)/sum(rate); %求贡献率 contr' %显示贡献率 num=input('请输入主成分个数:'); %交互式选取主成分个数 df=X*vec(:,1:num); %计算各主成的得分 tf=df*rate(1:num)/100; %计算综合得分 [stf,ind]=sort(tf,'descend'); %把得分按照降序排列 [ind,stf] %显示排名程序理解

X=zscore(data); 来自知乎

在这里插入图片描述

R=corrcoef(X); 12、13函数

在这里插入图片描述

在这里插入图片描述 matlab中princomp,pcacov,pcares,barttest四大分析函数的应用如下：

1.princomp

功能：主成分分析格式：PC=princomp(X) [PC,SCORE,latent,tsquare]=princomp(X)

说明：[PC,SCORE,latent,tsquare]=princomp(X)对数据矩阵X进行主成分分析，给出各主成分(PC)、所谓的Z-得分 (SCORE)、X的方差矩阵的特征值(latent)和每个数据点的HotellingT2统计量(tsquare)。

2.pcacov

1.功能：运用协方差矩阵进行主成分分析格式：PC=pcacov(X)

[PC,latent,explained]=pcacov(X)

说明：[PC,latent,explained]=pcacov(X) 通过协方差矩阵X进行主成分分析返回主成分(PC)、协方差矩阵X的特征值(latent)和每个特征向量表征在观测量总方差中所占的百分数(explained)。

3.pcares

功能：主成分分析的残差格式：residuals=pcares(X,ndim)

说明：pcares(X,ndim)返回保留X的ndim个主成分所获的残差。注意，ndim是一个标量，必须小于X的列数。而且，X是数据矩阵，而不是协方差矩阵。

4.barttest

功能：主成分的巴特力特检验格式：ndim=barttest(X,alpha) [ndim,prob,chisquare]=barttest(X,alpha)

说明：巴特力特检验是一种等方差性检验。 ndim=barttest(X,alpha)是在显著性水平alpha下，给出满足数据矩阵X的非随机变量的n维模型，ndim即模型维数，它由一系列假设检验所确定，ndim=1表明数据X对应于每个主成分的方差是相同的；ndim=2表明数据X对应于第二成分及其余成分的方差是相同的。

因子分析相关性分析回归分析一元回归例题

在这里插入图片描述

clc,clear x=[594 638 1122 1155 1408 1595 1969 2078 2585 2530]; y=[800 1100 1400 1700 2000 2300 2600 2900 3200 3500]; plot(x,y,'*') %画出y-x散点图 x=x';Y=y'; X=[ones(10,1),x]; %构造回归分析的数据矩阵 [beta,betaint,r,rint,st]=regress(Y,X) %计算回归系数和统计量 %beta:回归系数,betaint:回归系数置信区间,r:残差,rint:残差0.95的置信区间 %st:x统计量，其分量对应R?、F 、P 、s? 聚类分析

【本文地址】

公司简介

联系我们