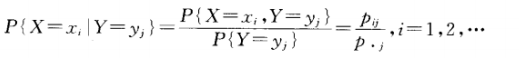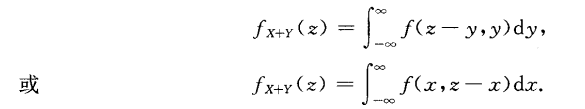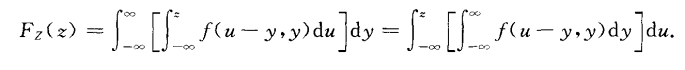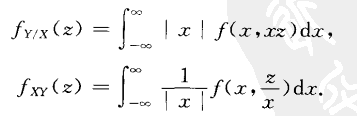概率论总结(二)：多维随机变量及其分布

您所在的位置：网站首页 › 一维连续随机变量在任何一个点上的概率都是零对吗 › 概率论总结(二)：多维随机变量及其分布

概率论总结(二)：多维随机变量及其分布

2024-05-29 03:22| 来源: 网络整理| 查看: 265

1.二维随机变量

根据随机变量的定义我们知道它其实是关于样本空间的函数，同样，二维随机变量也是关于样本空间的函数。只不过这里是关于样本空间的两个函数。比如样本空间是某地区全部学龄前儿童，那么它们的身高和体重就是关于样本空间的两个函数(或称映射)，所以它们也是定义在样本空间S上的两个随机变量。

一般来讲，多维的随机变量都是关于一个样本空间的。在机器学习中，常用多维随机变量描述一个事物的多重属性，然后用统计学知识(如朴素贝叶斯、贝叶斯网络)解决实际问题(如将事物进行分类)。

(1)离散型的二维随机变量

取值对(X,Y)的取值是也有限对或可列无限多对。同样常用分布律来描述二维离散型随机变量的分布。

(2)连续型的二维随机变量

(X,Y)的取值是无限多且不可列。常用联合分布函数和联合概率密度来描述二维离散型随机变量的分布。

2.联合分布函数和联合概率密度函数

我们知道一维随机变量的分布函数描述的是该变量X从负无穷到X=x的概率。对于二维随机变量来说，我们想要将（X，Y）作为一个整体进行研究，所以产生联合分布函数。他其实描述的是在(X，Y)的取值，以及事件在某个取值范围(矩形范围)发生的概率。

$F(x,y)=P\{(X \leq x) \cap (Y\leq y)\}=P(X \leq x, Y\leq y)$

$F(x,y)=\int _{-\infty}^{x}\int _{-\infty}^{y}f(u,v)dudv$

f(x,y)就称为联合概率密度函数。f(x,y)虽然不能表示取值X=x,Y=y的概率，但是他能表示点(X,Y)落在小长方形 $(x,x+\bigtriangleup x] * (y,y+\bigtriangleup y]$ 的可能性的高低(跟其他点相比)。特别地，当小长方形的长和宽都是1时，则点落在该长方形的概率就是 $f(x,y)\bigtriangleup x \bigtriangleup y=f(x,y)$

这里举一个二维正态分布的概率密度函数的例子：

如果(X，Y)服从二维正态分布，那么它的概率密度函数为：

$f(x,y)=\frac{1}{2\pi \sigma_1\sigma_2\sqrt{1-\rho^2} }exp\{\frac{-1}{2(1-\rho^2)}[\frac{(x-\mu_1)^2}{\rho_1^2}\\-2\rho \frac{(x-\mu_1)(y-\mu_2)}{\rho _1 \rho _2} +\frac{(y- \mu_2)^2}{\rho_2^2}]\}$

3.边缘分布和边缘概率密度

边缘分布其实就是多维随机变量中的其中一维随机变量的分布函数。

$F_X(x)=P\{X\leq x\} = P\{X \leq x,Y\infty\}=F(x,\infty)$

对于离散型而言

$F_X(x)=F(x,\infty)=\sum _{x_i\leq x}\sum_{j=1}^{\infty}p_{ij}$

对于连续型而言

$F_X(x)=F(x,\infty)=\int _{-\infty}^x[\int _{-\infty}^{\infty}f(x,y)dy]dx$

有了边缘分布函数，自然有边缘概率密度函数，根据定义及上面的式子有：

$f_X(x)=\int _{-\infty}^{\infty}f(x,y)dy$

y的情况也相同。

事实上，我们根据二维正态分布的概率密度，求出其边缘概率密度，发现边缘概率密度正是一维正态分布的的概率密度。

4.条件分布

条件分布是由条件概率而来的。

对于离散型而言，我们用条件分布律来描述。

对于连续型而言，它的分布函数就跟我们前面的推理不同。这是为什么呢？首先我们的首要任务是估计事件在某个取值附近发生的可能性大小，分布函数和概率密度函数的定义都是为估计该可能性大小而服务的。（在这里可能性大小用于点与点的比较，不代表概率大小）

由于连续型随机变量的特殊性，我们只能定义任意确定点的概率都是零，才能保证总体概率等于1的事实。所以用了概率密度来描述事件发生在该点的可能性，事实上，可以通过比较两个点的概率密度大小来比较事件发生在两个点的可能性大小(注意不是概率大小）。所以我们就定义这样一个概率密度来衡量。概率密度函数可以人为挑选，但他必须满足下面的式子。

对于一维变量：概率密度需要满足： $\int _{-\infty}^{\infty}f(t)dt=1$

对于二维变量：概率密度需要满足： $\int _{-\infty}^{\infty}\int _{-\infty}^{\infty}f(u,v)dudv=1$

在我的猜测中，数学家们应该是先定义了概率密度来衡量可能性大小，再引入分布函数，利用它们的差值求得一定范围内的概率的。

然后回到条件分布，我们想要衡量已知事件在Y维度上为Y=y，求其在X维度上X=x的可能性大小。那我们怎么去挑选这样一个概率密度函数呢，但是由于X，Y的概率密度函数以及它们的联合概率密度都已经确定，我们没有自己挑选的余地，只能根据已知量去求。

根据上面我们知道概率密度函数在某个区间的积分就是该区间的概率值，所以我们可以先求出任意区间的条件概率，然后根据概率反求出概率密度函数。

下面假设区间的长宽都是epsilon，那么区间上的条件概率，也就是已知事件在Y维度上范围是为(y,y+epsilon)，其在X维度上范围是(x,x+epsilon)的概率为：

$\frac {\int _{x_t}^{x_t+\epsilon}\int _{y_t}^{y_t+\epsilon}f(x,y)dxdy}{\int _{y_t}^{y_t+\epsilon}f_Y(y)dy}$

而由于 $\epsilon$ 极小，所以我们可以将上式转化为：

$\frac {\int _{x_t}^{x_t+\epsilon}[\int _{y_t}^{y_t+\epsilon}f(x,y)dy]dx}{\int _{y_t}^{y_t+\epsilon}f_Y(y)dy} =\frac{\epsilon \int _{x_t}^{x_t+\epsilon}f(x,y)dx}{\epsilon f_Y(y)}= \int _{x_t}^{x_t+\epsilon}\frac{f(x,y)}{ f_Y(y)}dx=\frac{f(x,y)}{ f_Y(y)} \epsilon$

回顾一维变量， $\int _{x}^{x+\epsilon}f(t)dt=f(t)\epsilon$ ，是事件发生在X=x附近的小区间的概率， $f(t)\quad or\quad f(x)$ 是概率密度，它可以用来衡量事件发生在X=x点的可能性大小。

根据相同的推理，根据上面式子， $\frac{f(x,y)}{ f_Y(y)}$ 就是条件概率密度，它可以衡量已知事件在Y维度上是y，求其在X维度上是x的可能性大小(注意不是概率大小）。

所以最终条件概率密度 $f_{X|Y}(x|y)=\frac{f(x,y)}{ f_Y(y)}$ 。经过证明它的积分 $\int _{-\infty}^{\infty}\frac{f(x,y)}{ f_Y(y)}dx$ 确实是等于1的。笔者发现这里的y只能是给定的值，而不是给定的范围。因为上面的epsilon之所以能直接抽取出来，正是因为该范围无限的小，区间内概率密度相同的假设才能成立。而范围无限的小，求极限之后就可以视作一个具体的值。