线性代数让我想想：快速求三阶矩阵的逆矩阵

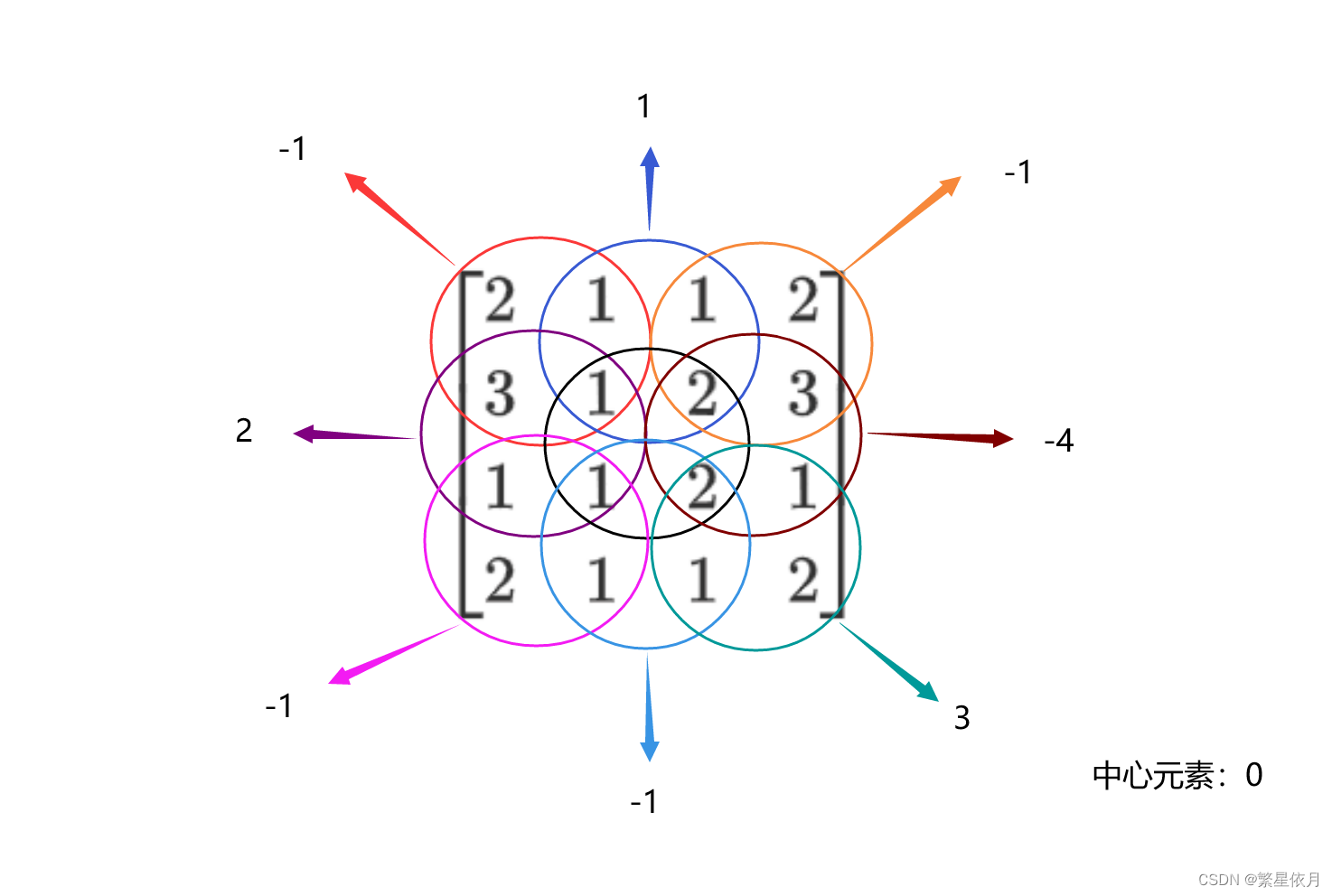
一般情况下，我们求解伴随矩阵是要注意符号问题和位置问题的（如下所示） A − 1 = 1 [    ] [ − [    ] − [    ] − [    ]    − [    ] ] = A − 1 = 1 [    ] [     M 11 − [ M 12 ]     M 13 − [ M 21 ]     M 22 − [ M 23 ]        M 31 − [ M 32 ]     M 33 ] ⊤ \begin{aligned} & A^{-1}=\frac{1}{[\ \ ]} \left[\begin{array}{cccccc} & -[\ \ ] & \\ -[\ \ ] & & -[\ \ ]\ \ \\ & -[\ \ ] & \\ \end{array}\right]= \\ \\ & A^{-1}=\frac{1}{[\ \ ]} \left[\begin{array}{cccccc} \ \ \ M_{11} & -[M_{12}] & \ \ \ M_{13}\\ -[M_{21}] & \ \ \ M_{22} & -[M_{23}]\ \ \\ \ \ \ M_{31} & -[M_{32}] & \ \ \ M_{33}\\ \end{array}\right]^\top\\ \end{aligned} ​A−1=[  ]1​⎣⎡​−[  ]​−[  ]−[  ]​−[  ]  ​⎦⎤​=A−1=[  ]1​⎣⎡​   M11​−[M21​]   M31​​−[M12​]   M22​−[M32​]​   M13​−[M23​]     M33​​⎦⎤​⊤​ 我们根据位置安排(行调换)的策略可以避免符号问题，将问题进行化简。

求矩阵 D D D 的逆矩阵 D = [ 2 1 1 1 2 1 2 3 1 ] D=\left[\begin{array}{lll} 2 & 1 & 1 \\ 1 & 2 & 1 \\ 2 & 3 & 1 \end{array}\right] D=⎣⎡​212​123​111​⎦⎤​ 我们把第一二列抄写到矩阵后面 D 1 = [ 2 1 1 2 1 1 2 1 1 2 2 3 1 2 3 ] D_1=\left[\begin{array}{lll|ll} 2 & 1 & 1 & 2 & 1 \\ 1 & 2 & 1 & 1 & 2 \\ 2 & 3 & 1 & 2 & 3 \end{array}\right] D1​=⎣⎡​212​123​111​212​123​⎦⎤​ 然后把第一二行抄写到矩阵下面（新矩阵 D 1 D_1 D1​ 的第一二行）， 这样我们就得到了一个五阶矩阵： D 2 = [ 2 1 1 2 1 1 2 1 1 2 2 3 1 2 3 2 1 1 2 1 1 2 1 1 2 ] = [ 2 1 1 2 1 1 2 1 1 2 2 3 1 2 3 2 1 1 2 1 1 2 1 1 2 ] D_2=\left[\begin{array}{lll|ll} 2 & 1 & 1 & 2 & 1 \\ 1 & 2 & 1 & 1 & 2 \\ 2 & 3 & 1 & 2 & 3 \\ \hline 2 & 1 & 1 & 2 & 1 \\ 1 & 2 & 1 & 1 & 2 \\ \end{array}\right]= \left[\begin{array}{lllll} \textcolor{cornflowerblue}{2} & \textcolor{cornflowerblue}{1} & \textcolor{cornflowerblue}{1} & \textcolor{cornflowerblue}{2} & \textcolor{cornflowerblue}{1} \\ \textcolor{cornflowerblue}{1} & 2 & 1 & 1 & 2 \\ \textcolor{cornflowerblue}{2} & 3 & 1 & 2 & 3 \\ \textcolor{cornflowerblue}{2} & 1 & 1 & 2 & 1 \\ \textcolor{cornflowerblue}{1} & 2 & 1 & 1 & 2 \\ \end{array}\right] D2​=⎣⎢⎢⎢⎢⎡​21221​12312​11111​21221​12312​​⎦⎥⎥⎥⎥⎤​=⎣⎢⎢⎢⎢⎡​21221​12312​11111​21221​12312​⎦⎥⎥⎥⎥⎤​ 然后我们把第一行和第一列删除（新矩阵 D 2 D_2 D2​ 的第一行和第一列，将标蓝的元素删除） D 3 = [ 2 1 1 2 3 1 2 3 1 1 2 1 2 1 1 2 ] D_3=\left[\begin{array}{lllll} 2 & 1 & 1 & 2 \\ 3 & 1 & 2 & 3 \\ 1 & 1 & 2 & 1 \\ 2 & 1 & 1 & 2 \\ \end{array}\right] D3​=⎣⎢⎢⎡​2312​1111​1221​2312​⎦⎥⎥⎤​ 然后我们算出矩阵分块组成的九个二阶行列式：

然后我们将求出的九个行列式结果填充到伴随矩阵的框架里，记得加上转置符号 [ − 1     1 − 1     2     0 − 4 − 1 − 1     2 ] ⊤ = [ − 1     2 − 1     1     0 − 1 − 1 − 4     2 ] \left[\begin{array}{lllll} -1 &\ \ \ 1 & -1 \\ \ \ \ 2 &\ \ \ 0 & -4 \\ -1 & -1 &\ \ \ 2 \\ \end{array}\right]^\top= \left[\begin{array}{lllll} -1 &\ \ \ 2 & -1 \\ \ \ \ 1 &\ \ \ 0 & -1 \\ -1 & -4 &\ \ \ 2 \\ \end{array}\right] ⎣⎡​−1   2−1​   1   0−1​−1−4   2​⎦⎤​⊤=⎣⎡​−1   1−1​   2   0−4​−1−1   2​⎦⎤​ 这样我们就得到了伴随矩阵，然后计算矩阵对应的行列式 ∣ D ∣ = − 2 |D|=-2 ∣D∣=−2，

最后根据公式 A − 1 = 1 ∣ A ∣ A ∗ A^{-1}=\frac{1}{|A|}A^* A−1=∣A∣1​A∗，求出逆矩阵 D − 1 D^{-1} D−1 D − 1 = 1 ∣ D ∣ D ∗ =     1 − 2 [ − 1     2 − 1     1     0 − 1 − 1 − 4     2 ] = [     1 2 − 1     1 2 − 1 2     0     1 2     1 2     2 − 1 ] D^{-1}=\frac{1}{|D|}D^*=\frac{\ \ \ 1}{-2} \left[\begin{array}{lllll} -1 &\ \ \ 2 & -1 \\ \ \ \ 1 &\ \ \ 0 & -1 \\ -1 & -4 &\ \ \ 2 \\ \end{array}\right]= \left[\begin{array}{lllll} \ \ \ \frac{1}{2} &-1 & \ \ \ \frac{1}{2} \\ -\frac{1}{2} &\ \ \ 0 & \ \ \ \frac{1}{2} \\ \ \ \ \frac{1}{2} &\ \ \ 2 & -1 \\ \end{array}\right] D−1=∣D∣1​D∗=−2   1​⎣⎡​−1   1−1​   2   0−4​−1−1   2​⎦⎤​=⎣⎡​   21​−21​   21​​−1   0   2​   21​   21​−1​⎦⎤​

求矩阵 A A A 的逆矩阵 A = [ 1 1 1 4 2 1 9 3 1 ] A=\left[\begin{array}{lll} 1 & 1 & 1 \\ 4 & 2 & 1 \\ 9 & 3 & 1 \end{array}\right] A=⎣⎡​149​123​111​⎦⎤​ 抄写后对应的五阶矩阵为： A 1 = [ 1 1 1 1 1 4 2 1 4 2 9 3 1 9 3 1 1 1 1 1 4 2 1 4 2 ] A_1=\left[\begin{array}{lll} 1 & 1 & 1 &1 & 1\\ 4 & 2 & 1 &4 & 2\\ 9 & 3 & 1 &9 & 3\\ 1 & 1 & 1 &1 & 1\\ 4 & 2 & 1 &4 & 2 \end{array}\right] A1​=⎣⎢⎢⎢⎢⎡​14914​12312​11111​14914​12312​⎦⎥⎥⎥⎥⎤​ 删除后得到的四阶矩阵为： A 2 = [ 2 1 4 2 3 1 9 3 1 1 1 1 2 1 4 2 ] A_2=\left[\begin{array}{lll} 2 & 1 &4 & 2\\ 3 & 1 &9 & 3\\ 1 & 1 &1 & 1\\ 2 & 1 &4 & 2 \end{array}\right] A2​=⎣⎢⎢⎡​2312​1111​4914​2312​⎦⎥⎥⎤​ 那么对应的伴随矩阵为： A ∗ = [ − 1     5 − 6     2 − 8     6 − 1     3 − 2 ] ⊤ = [ − 1     2 − 1     5 − 8     3 − 6     6 − 2 ] A^*=\left[\begin{array}{lllll} -1 &\ \ \ 5 & -6 \\ \ \ \ 2 & -8 & \ \ \ 6 \\ -1 & \ \ \ 3 & -2 \\ \end{array}\right]^\top= \left[\begin{array}{lllll} -1 &\ \ \ 2 & -1 \\ \ \ \ 5 & -8 & \ \ \ 3 \\ -6& \ \ \ 6 & -2 \\ \end{array}\right] A∗=⎣⎡​−1   2−1​   5−8   3​−6   6−2​⎦⎤​⊤=⎣⎡​−1   5−6​   2−8   6​−1   3−2​⎦⎤​ 矩阵对应的行列式为 ∣ A ∣ = − 2 |A|=-2 ∣A∣=−2，根据公式计算得到逆矩阵： A − 1 = 1 ∣ A ∣ A ∗ =     1 − 2 [ − 1     2 − 1     5 − 8     3 − 6     6 − 2 ] = [     1 2 − 1     1 2 − 5 2     4 − 3 2     3 − 3     1 2 ] A^{-1}=\frac{1}{|A|}A^*=\frac{\ \ \ 1}{-2} \left[\begin{array}{lllll} -1 &\ \ \ 2 & -1 \\ \ \ \ 5 & -8 & \ \ \ 3 \\ -6& \ \ \ 6 & -2 \\ \end{array}\right]= \left[\begin{array}{lllll} \ \ \ \frac{1}{2} &-1 & \ \ \ \frac{1}{2} \\ -\frac{5}{2} &\ \ \ 4 & -\frac{3}{2} \\ \ \ \ 3 & -3 & \ \ \ \frac{1}{2} \\ \end{array}\right] A−1=∣A∣1​A∗=−2   1​⎣⎡​−1   5−6​   2−8   6​−1   3−2​⎦⎤​=⎣⎡​   21​−25​   3​−1   4−3​   21​−23​   21​​⎦⎤​